人教版数学八年级上册 11.3 多边形及其内角和 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 11.3 多边形及其内角和 同步练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 275.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 22:51:18 | ||
图片预览


文档简介
《11.3
多边形及其内角和》
同步训练题
基础题训练(一):限时30分钟
1.如图,AC,BD为四边形ABCD的对角线,∠ABC=90°,∠ABD+∠ADB=∠ACB,∠ADC=∠BCD.
(1)求证:AD⊥AC;
(2)探求∠BAC与∠ACD之间的数量关系,并说明理由.
2.将纸片△ABC沿DE折叠使点A落在点A'处
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是
;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为
.
3.【知识回顾】:
如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD=
.
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB=
°.(直接写出答案)
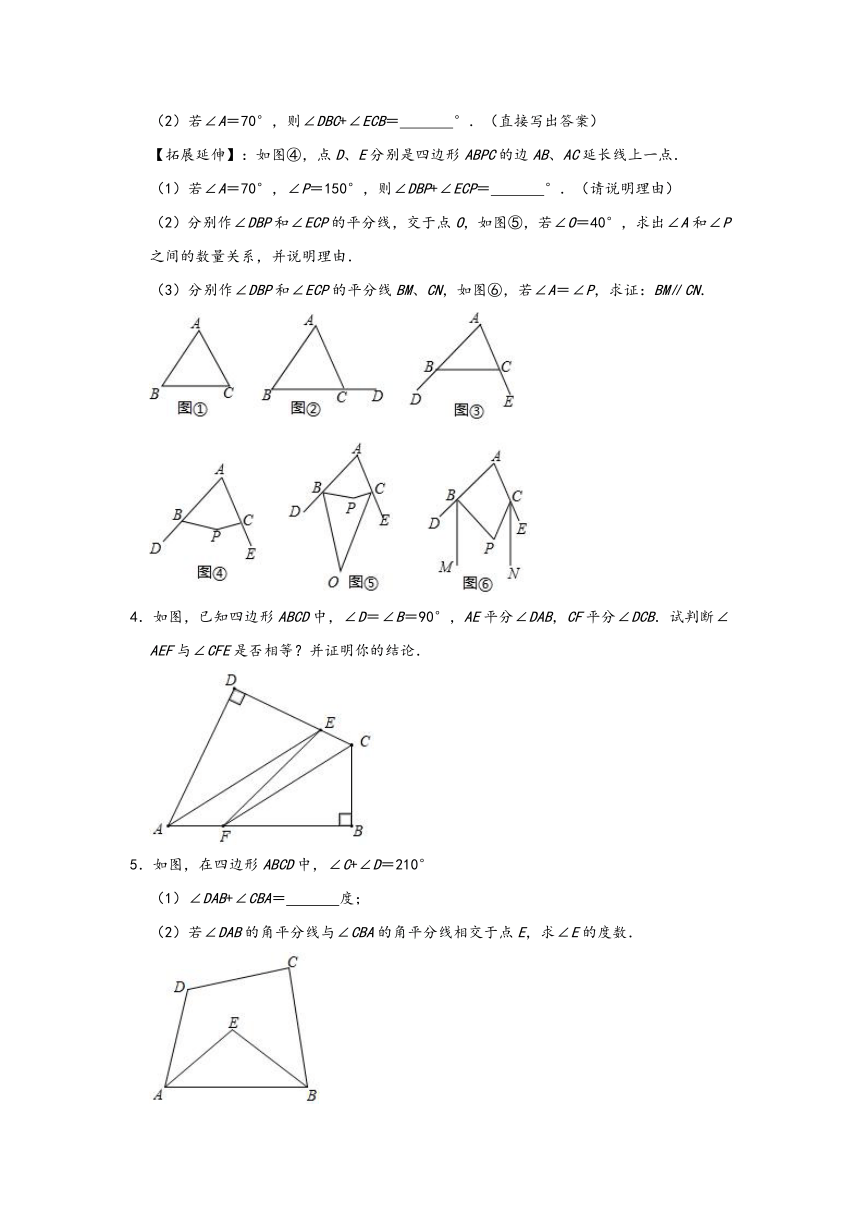
(2)若∠A=70°,则∠DBC+∠ECB=
°.(直接写出答案)
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP=
°.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
4.如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB.试判断∠AEF与∠CFE是否相等?并证明你的结论.
5.如图,在四边形ABCD中,∠C+∠D=210°
(1)∠DAB+∠CBA=
度;
(2)若∠DAB的角平分线与∠CBA的角平分线相交于点E,求∠E的度数.
基础题训练(二):限时30分钟
6.如图,在四边形ABCD中,∠A=∠C=90°,BE∥DF,∠1=∠2.求证:∠3=∠4.
7.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
8.(1)如图1,在△ADC中,∠ADC的平分线和∠ACD的外角平分线交于点P,若∠ADC=70°,∠ACD=50°,求∠P的度数.
(2)如图2,在四边形ABCD中,∠ADC的平分线和∠BCD的外角平分线交于点P,∠A=90°,∠B=150°,求∠P的度数.
(3)如图3,若将(2)中“∠A=90°,∠B=150°”改为“∠A=α,∠B=β”,其余条件不变,直接写出∠P与α+β之间的数量关系.
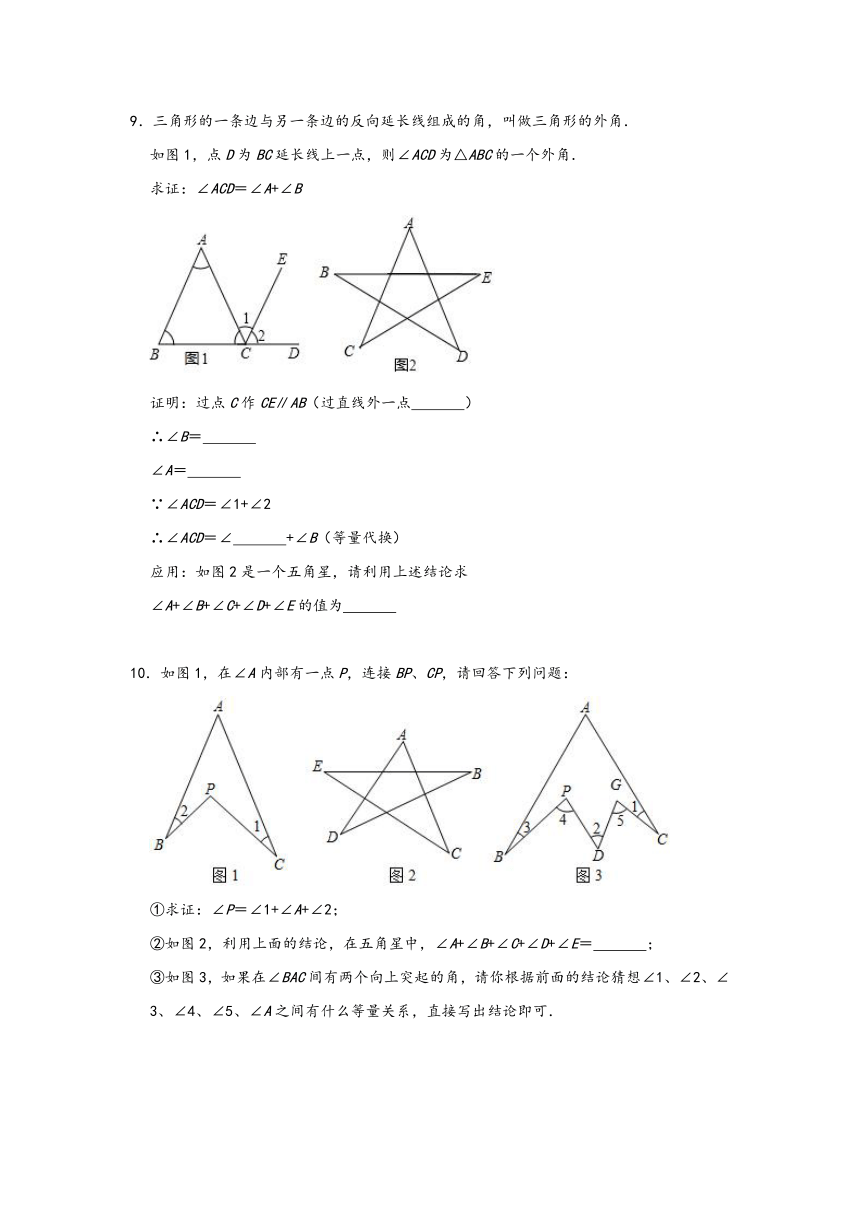
9.三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角.
如图1,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.
求证:∠ACD=∠A+∠B
证明:过点C作CE∥AB(过直线外一点
)
∴∠B=
∠A=
∵∠ACD=∠1+∠2
∴∠ACD=∠
+∠B(等量代换)
应用:如图2是一个五角星,请利用上述结论求
∠A+∠B+∠C+∠D+∠E的值为
10.如图1,在∠A内部有一点P,连接BP、CP,请回答下列问题:
①求证:∠P=∠1+∠A+∠2;
②如图2,利用上面的结论,在五角星中,∠A+∠B+∠C+∠D+∠E=
;
③如图3,如果在∠BAC间有两个向上突起的角,请你根据前面的结论猜想∠1、∠2、∠3、∠4、∠5、∠A之间有什么等量关系,直接写出结论即可.
基础题训练(三):限时30分钟
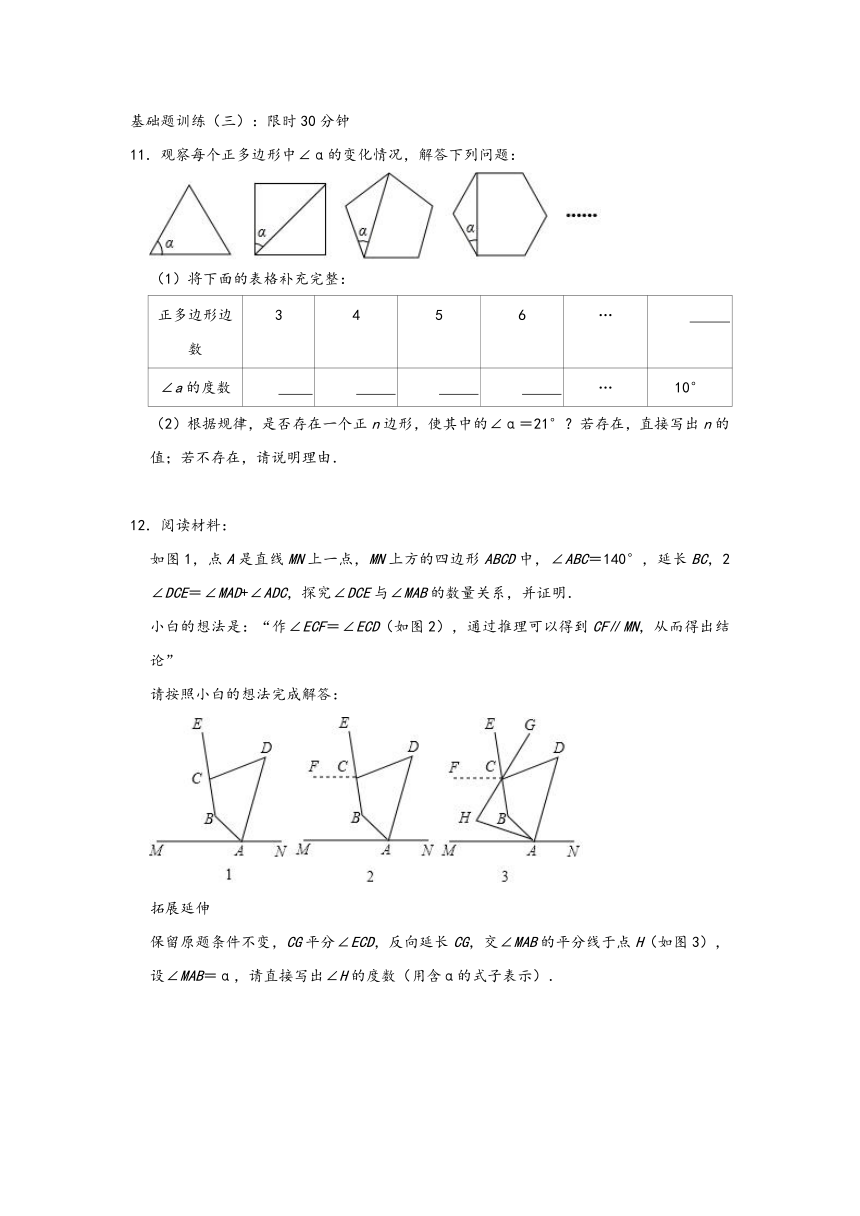
11.观察每个正多边形中∠α的变化情况,解答下列问题:
(1)将下面的表格补充完整:
正多边形边数
3
4
5
6
…
∠a的度数
…
10°
(2)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.
12.阅读材料:
如图1,点A是直线MN上一点,MN上方的四边形ABCD中,∠ABC=140°,延长BC,2∠DCE=∠MAD+∠ADC,探究∠DCE与∠MAB的数量关系,并证明.
小白的想法是:“作∠ECF=∠ECD(如图2),通过推理可以得到CF∥MN,从而得出结论”
请按照小白的想法完成解答:
拓展延伸
保留原题条件不变,CG平分∠ECD,反向延长CG,交∠MAB的平分线于点H(如图3),设∠MAB=α,请直接写出∠H的度数(用含α的式子表示).
13.(1)思考探究:如图①,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,请探究∠P与∠A的关系是
.
(2)类比探究:如图②,四边形ABCD中,设∠A=α,∠D=β,α+β>180°,四边形ABCD的内角∠ABC与外角∠DCE的平分线相交于点P.求∠P的度数.(用α,β的代数式表示)
(3)拓展迁移:如图③,将(2)中α+β>180°改为α+β<180°,其它条件不变,请在图③中画出∠P,并直接写出∠P=
.(用α,β的代数式表示)
14.如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,且CE交AD于点F,∠EAD和∠ECD的角平分线相交于点P.
(1)求证:①AB∥CD;②∠EAD+∠ECD=2∠APC;
(2)若∠B=70°,∠E=60°,求∠APC的度数;
(3)若∠APC=m°,∠EFD=n°,请你探究m和n之间的数量关系.
15.如图1,在四边形ABCD中,∠A=∠C,点E在AB边上,DE平分∠ADC,且∠ADE=∠DEA.
(1)求证:AD∥BC;
(2)如图2,已知DF⊥BC交BC边于点G,交AB边的延长线于点F,且DB平分∠EDF.若∠BDC<45°,试比较∠F与∠EDF的大小,并说明理由.
参考答案
1.解:(1)∵在△ABC中,∠ABC=90°,
∴∠ACB+∠BAC=90°,
在△ABD中,
∠ABD+∠ADB+∠BAD=180°,
∵∠ABD+∠ADB=∠ACB,
∴∠ACB+∠BAD=180°,
即∠ACB+∠BAC+∠CAD=180°,
∴∠CAD=90°,
∴AD⊥AC.
(2)∠BAC=2∠ACD;
∵∠ABC=90°,
∴∠BAC=90°﹣∠ACB=90°﹣(∠BCD﹣∠ACD),
∵∠DAC=90°,
∴∠ADC=90°﹣∠ACD,
∵∠ADC=∠BCD,
∴∠BCD=90°﹣∠ACD,
∴∠BAC=90°﹣(90°﹣∠ACD﹣∠ACD)=2∠ACD.
2.解:(1)如图①,∠1=2∠A.
理由如下:由折叠知识可得:∠EA′D=∠A;
∵∠1=∠A+∠EA′D,
∴∠1=2∠A.
(2)如图②,2∠A=∠1+∠2.
理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,
∠A+∠A′+∠A′DA+∠A′EA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得:∠A=∠A′,
∴2∠A=∠1+∠2.
(3)如图③,
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1﹣∠2=56°,
解得∠A=28°.
故答案为:∠1=2∠A;28°.
3.解:【知识回顾】
∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠B;
故答案为:∠A+∠B;
【初步运用】
(1)∵∠DBC=∠A+∠ACB,∠A=70°,∠DBC=150°,
∴∠ACB=∠DBC﹣∠A=150°﹣70°=80°;
故答案为:80;
(2)∵∠A=70°,
∴∠ABC+∠ACB=110°,
∴∠DBC+∠ECB=360°﹣110°=250°,
故答案为:250;
【拓展延伸】
(1)如图④,连接AP,∵∠DBP=∠BAP+∠APB,∠ECP=∠CAP+∠APC,
∴∠DBP+∠ECP=∠BAP+∠APB+∠CAP+∠APC=∠BAC+∠BPC,
∵∠BAC=70°,∠BPC=150°,
∴∠DBP+∠ECP=∠BAC+∠BPC=70°+150°=220°,
故答案为:220;
(2)∠A和∠P之间的数量关系是:∠P=∠A+80°,
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=40°,
∴∠P=∠A+80°;
(3)证明:如图,延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN.
4.解:∠AEF=∠CFE.
证明:∵∠D=∠B=90°,
∴∠DAB+∠DCB=180°,
又∵AE平分∠DAB,CF平分∠DCB,
∴∠DAE=∠DAB,∠DCF=∠DCB,
∴∠DAE+∠DCF=(∠DAB+∠DCB)=90°,
∵∠D=90°,
∴∠DAE+∠DEA=90°,
∴∠DEA=∠DCF,
∴AE∥CF,
∴∠AEF=∠CFE.
5.解:(1)∵∠DAB+∠CBA+∠C+∠D=360°,
∴∠DAB+∠CBA=360°﹣(∠C+∠D)=360°﹣210°=150°.
故答案为:150;
(2)∵∠DAB与∠ABC的平分线交于四边形内一点E,
∴∠EAB=∠DAB,∠EBA=∠ABC,
∴∠E=180°﹣(∠EAB+∠EBA)
=180°﹣(∠DAB+∠CBA)
=180°﹣(360°﹣∠C﹣∠D)
=(∠C+∠D),
∵∠C+∠D=210°,
∴∠E=(∠C+∠D)=105°.
6.证明:∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE∥DF,
∴∠2=∠5,∠AEB=∠3,
∵∠1=∠2,
∴∠1=∠5,
∴∠AEB=∠4,
∴∠3=∠4.
7.解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
8.解:(1)如图1,在射线DC上取一点E,
∵∠ADC的平分线和∠ACD的平分线交于点P,
∴,
,
∴∠P=∠PCE﹣∠PDC=30°;
(2)如图2,在射线DC上取一点E,
∵∠ADC的平分线和∠BCD的外角平分线交于点P,
∴,
,
∴∠P=∠PCE﹣∠PDC
=
=
=
=
=
=30°;
(3).
9.证明:过点C作CE∥AB(过直线外一点有且只有一条直线与已知直线平行)
∴∠B=∠2(两直线平行,同位角相等),
∠A=∠1(两直线平行,内错角相等),
∵∠ACD=∠1+∠2,
∴∠ACD=∠A+∠B(等量代换)
应用:对于△BDN,∠MNA=∠B+∠D,
对于△CEM,∠NMA=∠C+∠E,
对于△ANM,∠A+∠MNA+∠NMA=180°,
∴∠A+∠B+∠D+∠C+∠E=180.
故答案为:有且只有一条直线与已知直线平行;∠2(两直线平行,同位角相等);∠1(两直线平行,内错角相等);A;180°
10.解:①连接AP并延长,则∠3=∠2+∠BAP,∠4=∠1+∠PAC,
故∠BPC=∠1+∠A+∠2;
②利用①中的结论,可得∠1=∠A+∠C+∠D,
∵∠2=∠B+∠E,
∵∠1+∠2=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
③连接AP、AD、AG并延长,
同①由三角形内角与外角的性质可求出∠4+∠5=∠1+∠2+∠3+∠BAC.
故答案为:180°.
11.解:(1)填表如下:
正多边形的边数
3
4
5
6
…
18
∠α的度数
60°
45°
36°
30°
…
10°
故答案为:60°,45°,36°,30°,18;
(2)不存在,理由如下:
假设存在正
n
边形使得∠α=21°,得∠α=()°=21°,
解得:n=8,又
n
是正整数,
所以不存在正
n
边形使得∠α=21°.
12.解:阅读材料:延长CB交MN于点T,
∵∠ECF=∠ECD,2∠DCE=∠MAD+∠ADC,
∴2∠ECD=∠MAD+∠ADC=360°﹣∠CTA﹣∠DCT=360°﹣(180°﹣∠MTC)﹣(180°﹣∠ECD)=∠MTC+∠ECD,
∴∠ECD=∠MTC,
∴∠ECF=∠MTC,
∴CF∥MN,
∵∠ABC=140°,
∴∠ABT=40°,
∴∠MTC=∠MAB+40°,
即∠DCE=∠MAB+40°;
拓展延伸:∠H=360°﹣∠CDA﹣∠MAB﹣∠DAB﹣∠HCD=180°﹣[360°﹣(180°﹣∠ECD)﹣∠MAB﹣(180°﹣∠ECD)]=180°﹣(∠ECD﹣∠MAB),
∵∠DCE=∠MAB+40°,
∴∠H=180°﹣(∠MAB+60°),
∵∠MAB=α,
∴∠H=120°﹣α.
13.解:(1)如图1中,结论:2∠P=∠A.
理由:∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴2∠PCD=∠ACD,2∠PBC=∠ABC,
∴2(∠P+∠PBC)=∠A+∠ABC,
2∠P+2∠PBC=∠A+∠ABC,
2∠P+∠ABC=∠A+∠ABC,
∴2∠P=∠A;
(2)如图2中,
解法一:由四边形内角和定理得,∠BCD=360°﹣∠A﹣∠D﹣∠ABC,
∴∠DCE=180°﹣(360°﹣∠A﹣∠D﹣∠ABC)=∠A+∠D+∠ABC﹣180°,
由三角形的外角性质得∠PCE=∠P+∠PBC,
∵BP、CP分别是∠ABC和∠DCE的平分线,
∴∠PBC=∠ABC,∠PCE=∠DCE,
∴∠P+∠PBC=(∠A+∠D+∠ABC﹣180°)=(∠A+∠D)+∠ABC﹣90°,
∴∠P=(∠A+∠D)﹣90°,
∵∠A=α,∠D=β,
∴∠P=(α+β)﹣90°;
解法二:延长BA交CD的延长线于F.
∵∠F=180°﹣∠FAD﹣∠FDA=180°﹣(180°﹣α)﹣(180°﹣β)=α+β﹣180°,
由(1)可知:∠P=∠F,
∴∠P=(α+β)﹣90°;
②如图3,延长AB交DC的延长线于F.
∵∠F=180°﹣α﹣β,∠P=∠F,
∴∠P=(180°﹣α﹣β)=90°﹣α﹣β.
故答案为:2∠P=∠A;90°﹣α﹣β.
14.解:(1)证明:①∵AD∥BC,∴∠EAD=∠B,
∵∠B=∠D,∴∠EAD=∠D,
∴AB∥CD;
②过点P作PQ∥AB,则∠EAP=∠APQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵∠EAP=∠EAD,∠DCP=,
∴;
(2)由(1)知AD∥BC,AB∥CD,
∴∠EAD=∠B=70°,∠ECD=∠E=60°,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠APC=;
(3)过点F作FH∥AB,则∠EAD=∠AFH,
∵AB∥CD,
∴FH∥CD,
∴∠ECD=∠CFH,
∴∠EAD+∠ECD=∠AFH+∠CFH=∠AFC=∠EFD,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠EFD=2∠APC,
∵∠APC=m°,∠EFD=n°,
∴.
15.解:(1)证明:∵DE平分∠ADC,
∴∠CDE=∠ADE,
又∵∠ADE=∠DEA,
∴∠CDE=∠DEA,
∴CD∥AB,
∴∠B+∠C=180°,
又∵∠A=∠C,
∴∠B+∠A=180°,
∴AD∥BC;
(2)∵DF⊥BC,
∴∠BGF=90°,
又∵AD∥BC,
∴∠ADF=∠BGF=90°,
∵CD∥AB,
∴∠CDF=∠F.
设∠EDB=∠BDF=x°,∠CDF=∠F=y°,
则∠EDF=2x°,∠ADE=∠EDC=(2x+y)°,
由∠ADF=∠ADE+∠EDF,得
2x+y+2x=90,
∴y=90﹣4x,
∴∠F﹣∠EDF=y°﹣2x°=90°﹣4x°﹣2x°=90°﹣6x,
∵∠BDC<45°,
∴x+y<45°,
x+90﹣4x<45,
解得x>15,
∴6x>90.
∴∠F﹣∠EDF=90°﹣6x°<0,
∴∠F<∠EDF.
多边形及其内角和》
同步训练题
基础题训练(一):限时30分钟
1.如图,AC,BD为四边形ABCD的对角线,∠ABC=90°,∠ABD+∠ADB=∠ACB,∠ADC=∠BCD.
(1)求证:AD⊥AC;
(2)探求∠BAC与∠ACD之间的数量关系,并说明理由.
2.将纸片△ABC沿DE折叠使点A落在点A'处
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是
;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为
.
3.【知识回顾】:
如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD=
.
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB=
°.(直接写出答案)
(2)若∠A=70°,则∠DBC+∠ECB=
°.(直接写出答案)
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP=
°.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
4.如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB.试判断∠AEF与∠CFE是否相等?并证明你的结论.
5.如图,在四边形ABCD中,∠C+∠D=210°
(1)∠DAB+∠CBA=
度;
(2)若∠DAB的角平分线与∠CBA的角平分线相交于点E,求∠E的度数.
基础题训练(二):限时30分钟
6.如图,在四边形ABCD中,∠A=∠C=90°,BE∥DF,∠1=∠2.求证:∠3=∠4.
7.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
8.(1)如图1,在△ADC中,∠ADC的平分线和∠ACD的外角平分线交于点P,若∠ADC=70°,∠ACD=50°,求∠P的度数.
(2)如图2,在四边形ABCD中,∠ADC的平分线和∠BCD的外角平分线交于点P,∠A=90°,∠B=150°,求∠P的度数.
(3)如图3,若将(2)中“∠A=90°,∠B=150°”改为“∠A=α,∠B=β”,其余条件不变,直接写出∠P与α+β之间的数量关系.
9.三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角.
如图1,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.
求证:∠ACD=∠A+∠B
证明:过点C作CE∥AB(过直线外一点
)
∴∠B=
∠A=
∵∠ACD=∠1+∠2
∴∠ACD=∠
+∠B(等量代换)
应用:如图2是一个五角星,请利用上述结论求
∠A+∠B+∠C+∠D+∠E的值为
10.如图1,在∠A内部有一点P,连接BP、CP,请回答下列问题:
①求证:∠P=∠1+∠A+∠2;
②如图2,利用上面的结论,在五角星中,∠A+∠B+∠C+∠D+∠E=
;
③如图3,如果在∠BAC间有两个向上突起的角,请你根据前面的结论猜想∠1、∠2、∠3、∠4、∠5、∠A之间有什么等量关系,直接写出结论即可.
基础题训练(三):限时30分钟
11.观察每个正多边形中∠α的变化情况,解答下列问题:
(1)将下面的表格补充完整:
正多边形边数
3
4
5
6
…
∠a的度数
…
10°
(2)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.
12.阅读材料:
如图1,点A是直线MN上一点,MN上方的四边形ABCD中,∠ABC=140°,延长BC,2∠DCE=∠MAD+∠ADC,探究∠DCE与∠MAB的数量关系,并证明.
小白的想法是:“作∠ECF=∠ECD(如图2),通过推理可以得到CF∥MN,从而得出结论”
请按照小白的想法完成解答:
拓展延伸
保留原题条件不变,CG平分∠ECD,反向延长CG,交∠MAB的平分线于点H(如图3),设∠MAB=α,请直接写出∠H的度数(用含α的式子表示).
13.(1)思考探究:如图①,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,请探究∠P与∠A的关系是
.
(2)类比探究:如图②,四边形ABCD中,设∠A=α,∠D=β,α+β>180°,四边形ABCD的内角∠ABC与外角∠DCE的平分线相交于点P.求∠P的度数.(用α,β的代数式表示)
(3)拓展迁移:如图③,将(2)中α+β>180°改为α+β<180°,其它条件不变,请在图③中画出∠P,并直接写出∠P=
.(用α,β的代数式表示)
14.如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,且CE交AD于点F,∠EAD和∠ECD的角平分线相交于点P.
(1)求证:①AB∥CD;②∠EAD+∠ECD=2∠APC;
(2)若∠B=70°,∠E=60°,求∠APC的度数;
(3)若∠APC=m°,∠EFD=n°,请你探究m和n之间的数量关系.
15.如图1,在四边形ABCD中,∠A=∠C,点E在AB边上,DE平分∠ADC,且∠ADE=∠DEA.
(1)求证:AD∥BC;
(2)如图2,已知DF⊥BC交BC边于点G,交AB边的延长线于点F,且DB平分∠EDF.若∠BDC<45°,试比较∠F与∠EDF的大小,并说明理由.
参考答案
1.解:(1)∵在△ABC中,∠ABC=90°,
∴∠ACB+∠BAC=90°,
在△ABD中,
∠ABD+∠ADB+∠BAD=180°,
∵∠ABD+∠ADB=∠ACB,
∴∠ACB+∠BAD=180°,
即∠ACB+∠BAC+∠CAD=180°,
∴∠CAD=90°,
∴AD⊥AC.
(2)∠BAC=2∠ACD;
∵∠ABC=90°,
∴∠BAC=90°﹣∠ACB=90°﹣(∠BCD﹣∠ACD),
∵∠DAC=90°,
∴∠ADC=90°﹣∠ACD,
∵∠ADC=∠BCD,
∴∠BCD=90°﹣∠ACD,
∴∠BAC=90°﹣(90°﹣∠ACD﹣∠ACD)=2∠ACD.
2.解:(1)如图①,∠1=2∠A.
理由如下:由折叠知识可得:∠EA′D=∠A;
∵∠1=∠A+∠EA′D,
∴∠1=2∠A.
(2)如图②,2∠A=∠1+∠2.
理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,
∠A+∠A′+∠A′DA+∠A′EA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得:∠A=∠A′,
∴2∠A=∠1+∠2.
(3)如图③,
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1﹣∠2=56°,
解得∠A=28°.
故答案为:∠1=2∠A;28°.
3.解:【知识回顾】
∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠B;
故答案为:∠A+∠B;
【初步运用】
(1)∵∠DBC=∠A+∠ACB,∠A=70°,∠DBC=150°,
∴∠ACB=∠DBC﹣∠A=150°﹣70°=80°;
故答案为:80;
(2)∵∠A=70°,
∴∠ABC+∠ACB=110°,
∴∠DBC+∠ECB=360°﹣110°=250°,
故答案为:250;
【拓展延伸】
(1)如图④,连接AP,∵∠DBP=∠BAP+∠APB,∠ECP=∠CAP+∠APC,
∴∠DBP+∠ECP=∠BAP+∠APB+∠CAP+∠APC=∠BAC+∠BPC,
∵∠BAC=70°,∠BPC=150°,
∴∠DBP+∠ECP=∠BAC+∠BPC=70°+150°=220°,
故答案为:220;
(2)∠A和∠P之间的数量关系是:∠P=∠A+80°,
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=40°,
∴∠P=∠A+80°;
(3)证明:如图,延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN.
4.解:∠AEF=∠CFE.
证明:∵∠D=∠B=90°,
∴∠DAB+∠DCB=180°,
又∵AE平分∠DAB,CF平分∠DCB,
∴∠DAE=∠DAB,∠DCF=∠DCB,
∴∠DAE+∠DCF=(∠DAB+∠DCB)=90°,
∵∠D=90°,
∴∠DAE+∠DEA=90°,
∴∠DEA=∠DCF,
∴AE∥CF,
∴∠AEF=∠CFE.
5.解:(1)∵∠DAB+∠CBA+∠C+∠D=360°,
∴∠DAB+∠CBA=360°﹣(∠C+∠D)=360°﹣210°=150°.
故答案为:150;
(2)∵∠DAB与∠ABC的平分线交于四边形内一点E,
∴∠EAB=∠DAB,∠EBA=∠ABC,
∴∠E=180°﹣(∠EAB+∠EBA)
=180°﹣(∠DAB+∠CBA)
=180°﹣(360°﹣∠C﹣∠D)
=(∠C+∠D),
∵∠C+∠D=210°,
∴∠E=(∠C+∠D)=105°.
6.证明:∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE∥DF,
∴∠2=∠5,∠AEB=∠3,
∵∠1=∠2,
∴∠1=∠5,
∴∠AEB=∠4,
∴∠3=∠4.
7.解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
8.解:(1)如图1,在射线DC上取一点E,
∵∠ADC的平分线和∠ACD的平分线交于点P,
∴,
,
∴∠P=∠PCE﹣∠PDC=30°;
(2)如图2,在射线DC上取一点E,
∵∠ADC的平分线和∠BCD的外角平分线交于点P,
∴,
,
∴∠P=∠PCE﹣∠PDC
=
=
=
=
=
=30°;
(3).
9.证明:过点C作CE∥AB(过直线外一点有且只有一条直线与已知直线平行)
∴∠B=∠2(两直线平行,同位角相等),
∠A=∠1(两直线平行,内错角相等),
∵∠ACD=∠1+∠2,
∴∠ACD=∠A+∠B(等量代换)
应用:对于△BDN,∠MNA=∠B+∠D,
对于△CEM,∠NMA=∠C+∠E,
对于△ANM,∠A+∠MNA+∠NMA=180°,
∴∠A+∠B+∠D+∠C+∠E=180.
故答案为:有且只有一条直线与已知直线平行;∠2(两直线平行,同位角相等);∠1(两直线平行,内错角相等);A;180°
10.解:①连接AP并延长,则∠3=∠2+∠BAP,∠4=∠1+∠PAC,
故∠BPC=∠1+∠A+∠2;
②利用①中的结论,可得∠1=∠A+∠C+∠D,
∵∠2=∠B+∠E,
∵∠1+∠2=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
③连接AP、AD、AG并延长,
同①由三角形内角与外角的性质可求出∠4+∠5=∠1+∠2+∠3+∠BAC.
故答案为:180°.
11.解:(1)填表如下:
正多边形的边数
3
4
5
6
…
18
∠α的度数
60°
45°
36°
30°
…
10°
故答案为:60°,45°,36°,30°,18;
(2)不存在,理由如下:
假设存在正
n
边形使得∠α=21°,得∠α=()°=21°,
解得:n=8,又
n
是正整数,
所以不存在正
n
边形使得∠α=21°.
12.解:阅读材料:延长CB交MN于点T,
∵∠ECF=∠ECD,2∠DCE=∠MAD+∠ADC,
∴2∠ECD=∠MAD+∠ADC=360°﹣∠CTA﹣∠DCT=360°﹣(180°﹣∠MTC)﹣(180°﹣∠ECD)=∠MTC+∠ECD,
∴∠ECD=∠MTC,
∴∠ECF=∠MTC,
∴CF∥MN,
∵∠ABC=140°,
∴∠ABT=40°,
∴∠MTC=∠MAB+40°,
即∠DCE=∠MAB+40°;
拓展延伸:∠H=360°﹣∠CDA﹣∠MAB﹣∠DAB﹣∠HCD=180°﹣[360°﹣(180°﹣∠ECD)﹣∠MAB﹣(180°﹣∠ECD)]=180°﹣(∠ECD﹣∠MAB),
∵∠DCE=∠MAB+40°,
∴∠H=180°﹣(∠MAB+60°),
∵∠MAB=α,
∴∠H=120°﹣α.
13.解:(1)如图1中,结论:2∠P=∠A.
理由:∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴2∠PCD=∠ACD,2∠PBC=∠ABC,
∴2(∠P+∠PBC)=∠A+∠ABC,
2∠P+2∠PBC=∠A+∠ABC,
2∠P+∠ABC=∠A+∠ABC,
∴2∠P=∠A;
(2)如图2中,
解法一:由四边形内角和定理得,∠BCD=360°﹣∠A﹣∠D﹣∠ABC,
∴∠DCE=180°﹣(360°﹣∠A﹣∠D﹣∠ABC)=∠A+∠D+∠ABC﹣180°,
由三角形的外角性质得∠PCE=∠P+∠PBC,
∵BP、CP分别是∠ABC和∠DCE的平分线,
∴∠PBC=∠ABC,∠PCE=∠DCE,
∴∠P+∠PBC=(∠A+∠D+∠ABC﹣180°)=(∠A+∠D)+∠ABC﹣90°,
∴∠P=(∠A+∠D)﹣90°,
∵∠A=α,∠D=β,
∴∠P=(α+β)﹣90°;
解法二:延长BA交CD的延长线于F.
∵∠F=180°﹣∠FAD﹣∠FDA=180°﹣(180°﹣α)﹣(180°﹣β)=α+β﹣180°,
由(1)可知:∠P=∠F,
∴∠P=(α+β)﹣90°;
②如图3,延长AB交DC的延长线于F.
∵∠F=180°﹣α﹣β,∠P=∠F,
∴∠P=(180°﹣α﹣β)=90°﹣α﹣β.
故答案为:2∠P=∠A;90°﹣α﹣β.
14.解:(1)证明:①∵AD∥BC,∴∠EAD=∠B,
∵∠B=∠D,∴∠EAD=∠D,
∴AB∥CD;
②过点P作PQ∥AB,则∠EAP=∠APQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵∠EAP=∠EAD,∠DCP=,
∴;
(2)由(1)知AD∥BC,AB∥CD,
∴∠EAD=∠B=70°,∠ECD=∠E=60°,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠APC=;
(3)过点F作FH∥AB,则∠EAD=∠AFH,
∵AB∥CD,
∴FH∥CD,
∴∠ECD=∠CFH,
∴∠EAD+∠ECD=∠AFH+∠CFH=∠AFC=∠EFD,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠EFD=2∠APC,
∵∠APC=m°,∠EFD=n°,
∴.
15.解:(1)证明:∵DE平分∠ADC,
∴∠CDE=∠ADE,
又∵∠ADE=∠DEA,
∴∠CDE=∠DEA,
∴CD∥AB,
∴∠B+∠C=180°,
又∵∠A=∠C,
∴∠B+∠A=180°,
∴AD∥BC;
(2)∵DF⊥BC,
∴∠BGF=90°,
又∵AD∥BC,
∴∠ADF=∠BGF=90°,
∵CD∥AB,
∴∠CDF=∠F.
设∠EDB=∠BDF=x°,∠CDF=∠F=y°,
则∠EDF=2x°,∠ADE=∠EDC=(2x+y)°,
由∠ADF=∠ADE+∠EDF,得
2x+y+2x=90,
∴y=90﹣4x,
∴∠F﹣∠EDF=y°﹣2x°=90°﹣4x°﹣2x°=90°﹣6x,
∵∠BDC<45°,
∴x+y<45°,
x+90﹣4x<45,
解得x>15,
∴6x>90.
∴∠F﹣∠EDF=90°﹣6x°<0,
∴∠F<∠EDF.
