湘教版数学九年级下册3.2 直棱柱、圆锥的侧面展开图教学课件(共31张PPT)
文档属性
| 名称 | 湘教版数学九年级下册3.2 直棱柱、圆锥的侧面展开图教学课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
直棱柱、圆锥的侧面展开图
教学课件
湘教版九年级下册
01
新课导入
新课导入
在日常生活中,我们能看到各种各样的包装盒,那它们的展开图是什么形状呢?展开图的面积又是多少呢?让我们一起来探索一下吧!
02
新知探究
新知探究
一.直棱柱的认识
底面图形边数
3
4
5
6
相应的立方体名称
直三
棱柱
直四
棱柱
直五
棱柱
直六
棱柱
底面是正多边形的棱柱是正棱柱.
新知探究
在几何中,我们把上述这样的立体图形称为直棱柱,其中“棱”是指两个面的公共边,
它具有以下特征:
(1)
有两个面互相平行,称它们为底面;
(2)其余各个面均为矩形,称它们为侧面;
(3)侧棱(指两个侧面的公共边)垂直于底面.
一.直棱柱的认识
新知探究
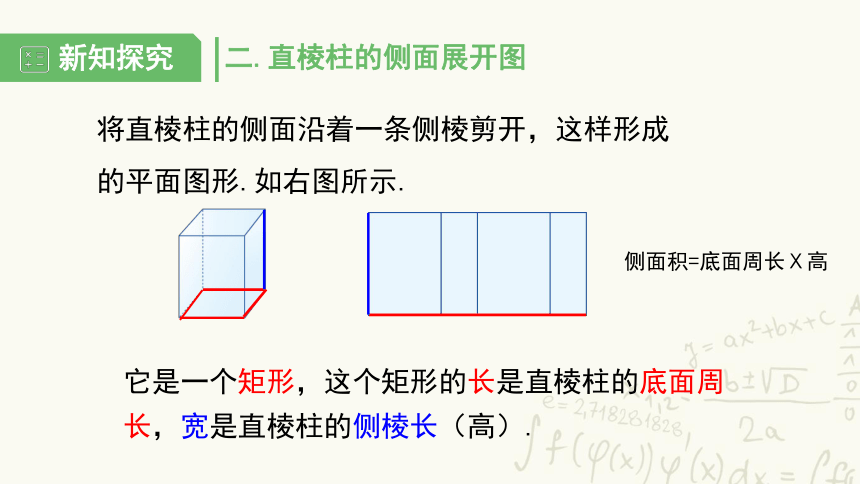
二.直棱柱的侧面展开图
将直棱柱的侧面沿着一条侧棱剪开,这样形成的平面图形.如右图所示.
它是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高).
侧面积=底面周长Ⅹ高
新知探究
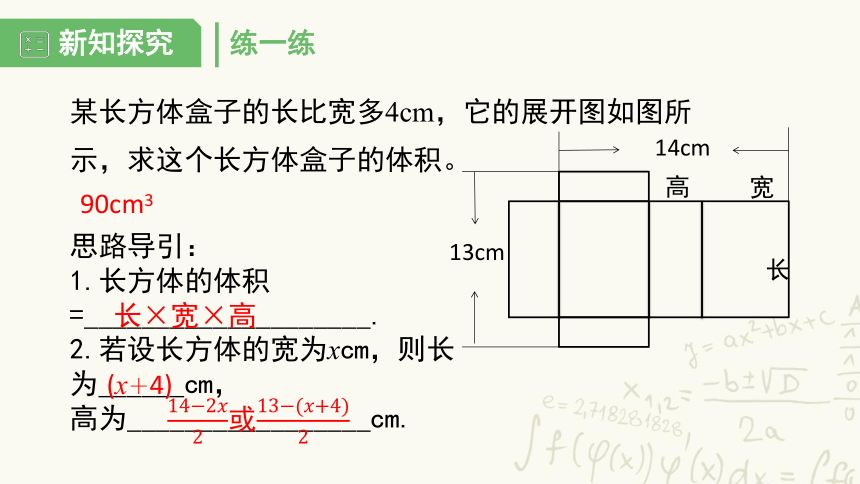
练一练
某长方体盒子的长比宽多4cm,它的展开图如图所示,求这个长方体盒子的体积。
高
宽
长
13cm
14cm
思路导引:
1.长方体的体积=____________________.
2.若设长方体的宽为xcm,则长为______cm,
高为_________________cm.
长×宽×高
(x+4)
或
90cm3
新知探究
解:设长方体盒子的宽为xcm,则长为
cm,
由题图可得
解得x=5
则长为5+4=9(cm),高为=2(cm)
体积为5×9×2=90(cm3)
故长方体的体积为90cm3.
(x+4)
新知探究
三.圆锥的认识
下图是雕塑与斗笠的形象,它们的形状有什么特点?
新知探究
三.圆锥的认识
1.在几何中,我们把上述这样的立体图形称为圆锥;
2.圆锥是由一个底面和一个侧面围成的图形,它的底面是一个圆,连接顶点与底面圆心的线段叫作圆锥的高;
3.圆锥顶点与底面圆上任意一点的连线都叫作圆锥的母线,母线的长度均相等.
如图,PO是圆锥的高.
PA是母线.
l
r
h
新知探究
四.圆锥的侧面展开图
l
o
r
圆锥的侧面展开图是什么图形?
扇形
圆锥的侧面展开图是扇形
新知探究
归纳总结
l
o
侧面
展开图
r
l
r
扇形
其侧面展开图扇形的半径=母线的长l
侧面展开图扇形的弧长=底面周长2
母线、高及底面半径间的关系
l2=h2+r2
h
新知探究
归纳总结
圆锥的侧面积计算公式
l
o
侧面
展开图
l
r
圆锥的全面积计算公式
(r表示圆锥底面的半径,
l
表示圆锥的母线长
)
=
新知探究
练一练
M
S
A
O
如图,圆锥底面的半径为10cm,高为10cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上的点A出发绕圆锥一周回到SA上的点M处,且SM=3AM,求它所走的最短距离。
500cm2
50cm
新知探究
练一练
M
S
A
O
思路导引:
1.圆锥的侧面展开图的扇形半径为______cm,弧长为______cm,圆锥的全面积=扇形的侧面积+___________.
2.所走的最短距离是圆锥侧面展开图中出发点与到达点之间的线段长度,
依据是__________________.
40
底面积
两点之间线段最短
新知探究
练一练
解:
(1)由题意,可得圆锥的母线SA==40cm
圆锥的侧面展开扇形的弧长l==20cm,
∴
S侧=l·SA=400cm2,
S底=·AO2=100cm2,
∴
S全=
S侧+
S底=(400+100)=500
S
A
A?
M
新知探究
练一练
解:
(2)沿母线SA将圆锥的侧面展开,如图,
则线段AM的长就是蚂蚁所走的最短距离。
由(1)知,SA=40cm,AA?的长为20cm,
设∠S=n°,
∴=20,
∴n=90,即∠S=90°,
∵SA?=SA=40cm,SM=3A?M,
∴SM=30cm.
在Rt△ASM中,由勾股定理得AM=50cm.
∴蚂蚁所走的最短距离是50cm.
S
A
A?
M
⌒
03
典型例题
典型例题
1.将正方体的表面沿某些棱剪开,展开成如图所示的平面图形,则原正方体中与“创”字所在的面相对的面上标的字是(
)
A
建
庆
大
力
魅
创
A.庆
B.力
C.大
D.魅
典型例题
2.一个圆柱的侧面展开图是边长为a的正方形,则这个圆柱的体积为(
)
A.
B.
C.
D.
A
典型例题
3.将一个无盖正方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是(
)
C
A
C
B
D
典型例题
4.
把一个用来盛爆米花的圆锥形纸杯沿母线剪开,得到一个半径为24cm,圆心角为120°的扇形,求该纸杯的底面半径和高度(结果保留根号)。
解:设该纸杯的底面半径为R,圆锥的高度为h,由题意可得
解得R=8cm
∴h==16(cm)
∴该纸杯的底面半径为8cm,高为16cm.
底面半径为8cm,高为16cm.
04
拓展提高
拓展提高
高
宽
长
14cm
13cm
某长方体包装盒的展开图如图所示,如果包装盒的表面积为146cm2,求这个包装盒的体积。
90cm3
拓展提高
解:设长方体的高为xcm,
由题意得
×2
=146,
整理得,,
解得=2,=-9(舍去),
∴长为9cm,宽为5cm,
长方体的体积为9×5×2=90(cm3).
答:这个包装盒的体积为90cm3.
05
课堂小结
课堂小结
06
作业布置
完成课本习题
3.2
A、B组
作业布置
谢
谢
观
看
直棱柱、圆锥的侧面展开图
教学课件
湘教版九年级下册
01
新课导入
新课导入
在日常生活中,我们能看到各种各样的包装盒,那它们的展开图是什么形状呢?展开图的面积又是多少呢?让我们一起来探索一下吧!
02
新知探究
新知探究
一.直棱柱的认识
底面图形边数
3
4
5
6
相应的立方体名称
直三
棱柱
直四
棱柱
直五
棱柱
直六
棱柱
底面是正多边形的棱柱是正棱柱.
新知探究
在几何中,我们把上述这样的立体图形称为直棱柱,其中“棱”是指两个面的公共边,
它具有以下特征:
(1)
有两个面互相平行,称它们为底面;
(2)其余各个面均为矩形,称它们为侧面;
(3)侧棱(指两个侧面的公共边)垂直于底面.
一.直棱柱的认识
新知探究
二.直棱柱的侧面展开图
将直棱柱的侧面沿着一条侧棱剪开,这样形成的平面图形.如右图所示.
它是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高).
侧面积=底面周长Ⅹ高
新知探究
练一练
某长方体盒子的长比宽多4cm,它的展开图如图所示,求这个长方体盒子的体积。
高
宽
长
13cm
14cm
思路导引:
1.长方体的体积=____________________.
2.若设长方体的宽为xcm,则长为______cm,
高为_________________cm.
长×宽×高
(x+4)
或
90cm3
新知探究
解:设长方体盒子的宽为xcm,则长为
cm,
由题图可得
解得x=5
则长为5+4=9(cm),高为=2(cm)
体积为5×9×2=90(cm3)
故长方体的体积为90cm3.
(x+4)
新知探究
三.圆锥的认识
下图是雕塑与斗笠的形象,它们的形状有什么特点?
新知探究
三.圆锥的认识
1.在几何中,我们把上述这样的立体图形称为圆锥;
2.圆锥是由一个底面和一个侧面围成的图形,它的底面是一个圆,连接顶点与底面圆心的线段叫作圆锥的高;
3.圆锥顶点与底面圆上任意一点的连线都叫作圆锥的母线,母线的长度均相等.
如图,PO是圆锥的高.
PA是母线.
l
r
h
新知探究
四.圆锥的侧面展开图
l
o
r
圆锥的侧面展开图是什么图形?
扇形
圆锥的侧面展开图是扇形
新知探究
归纳总结
l
o
侧面
展开图
r
l
r
扇形
其侧面展开图扇形的半径=母线的长l
侧面展开图扇形的弧长=底面周长2
母线、高及底面半径间的关系
l2=h2+r2
h
新知探究
归纳总结
圆锥的侧面积计算公式
l
o
侧面
展开图
l
r
圆锥的全面积计算公式
(r表示圆锥底面的半径,
l
表示圆锥的母线长
)
=
新知探究
练一练
M
S
A
O
如图,圆锥底面的半径为10cm,高为10cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上的点A出发绕圆锥一周回到SA上的点M处,且SM=3AM,求它所走的最短距离。
500cm2
50cm
新知探究
练一练
M
S
A
O
思路导引:
1.圆锥的侧面展开图的扇形半径为______cm,弧长为______cm,圆锥的全面积=扇形的侧面积+___________.
2.所走的最短距离是圆锥侧面展开图中出发点与到达点之间的线段长度,
依据是__________________.
40
底面积
两点之间线段最短
新知探究
练一练
解:
(1)由题意,可得圆锥的母线SA==40cm
圆锥的侧面展开扇形的弧长l==20cm,
∴
S侧=l·SA=400cm2,
S底=·AO2=100cm2,
∴
S全=
S侧+
S底=(400+100)=500
S
A
A?
M
新知探究
练一练
解:
(2)沿母线SA将圆锥的侧面展开,如图,
则线段AM的长就是蚂蚁所走的最短距离。
由(1)知,SA=40cm,AA?的长为20cm,
设∠S=n°,
∴=20,
∴n=90,即∠S=90°,
∵SA?=SA=40cm,SM=3A?M,
∴SM=30cm.
在Rt△ASM中,由勾股定理得AM=50cm.
∴蚂蚁所走的最短距离是50cm.
S
A
A?
M
⌒
03
典型例题
典型例题
1.将正方体的表面沿某些棱剪开,展开成如图所示的平面图形,则原正方体中与“创”字所在的面相对的面上标的字是(
)
A
建
庆
大
力
魅
创
A.庆
B.力
C.大
D.魅
典型例题
2.一个圆柱的侧面展开图是边长为a的正方形,则这个圆柱的体积为(
)
A.
B.
C.
D.
A
典型例题
3.将一个无盖正方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是(
)
C
A
C
B
D
典型例题
4.
把一个用来盛爆米花的圆锥形纸杯沿母线剪开,得到一个半径为24cm,圆心角为120°的扇形,求该纸杯的底面半径和高度(结果保留根号)。
解:设该纸杯的底面半径为R,圆锥的高度为h,由题意可得
解得R=8cm
∴h==16(cm)
∴该纸杯的底面半径为8cm,高为16cm.
底面半径为8cm,高为16cm.
04
拓展提高
拓展提高
高
宽
长
14cm
13cm
某长方体包装盒的展开图如图所示,如果包装盒的表面积为146cm2,求这个包装盒的体积。
90cm3
拓展提高
解:设长方体的高为xcm,
由题意得
×2
=146,
整理得,,
解得=2,=-9(舍去),
∴长为9cm,宽为5cm,
长方体的体积为9×5×2=90(cm3).
答:这个包装盒的体积为90cm3.
05
课堂小结
课堂小结
06
作业布置
完成课本习题
3.2
A、B组
作业布置
谢
谢
观
看
