湘教版数学九年级下册 3.3 三视图教学课件(共28张PPT)
文档属性
| 名称 | 湘教版数学九年级下册 3.3 三视图教学课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 22:58:26 | ||
图片预览





文档简介
(共28张PPT)
三视图
教学课件
湘教版九年级下册
01
新课导入
新课导入
这首诗教会了我们怎样观察物体(横看、侧看、近看、身处其中看),这类似于本节课所研究的内容——三视图。
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
——苏轼
02
新知探究
新知探究
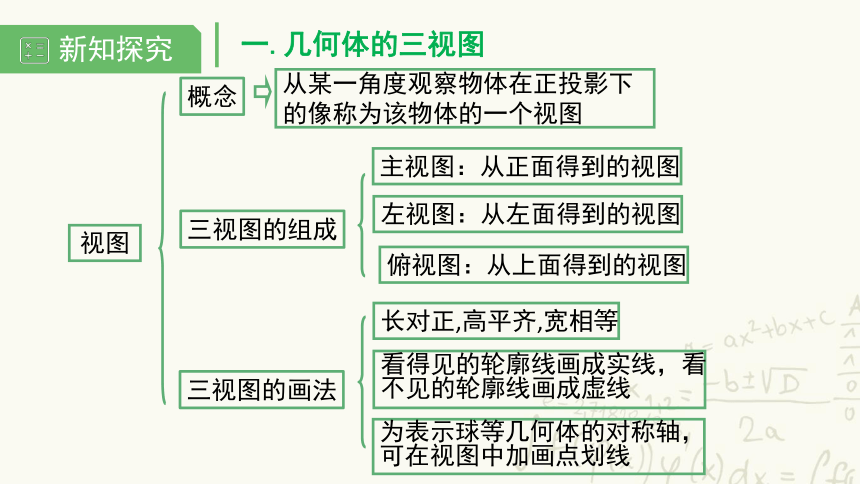
视图
从某一角度观察物体在正投影下
的像称为该物体的一个视图
主视图:从正面得到的视图
概念
三视图的组成
左视图:从左面得到的视图
俯视图:从上面得到的视图
三视图的画法
长对正,高平齐,宽相等
看得见的轮廓线画成实线,看
不见的轮廓线画成虚线
为表示球等几何体的对称轴,
可在视图中加画点划线
一.几何体的三视图
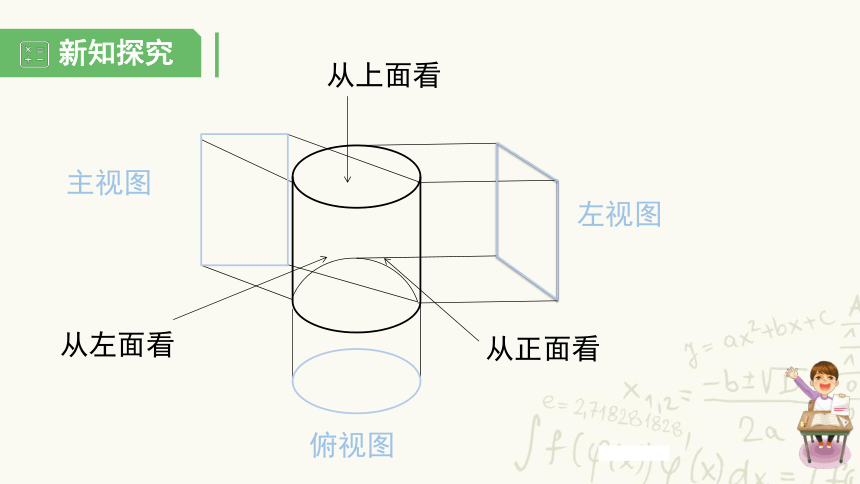
新知探究
俯视图
从上面看
从正面看
主视图
从左面看
左视图
新知探究
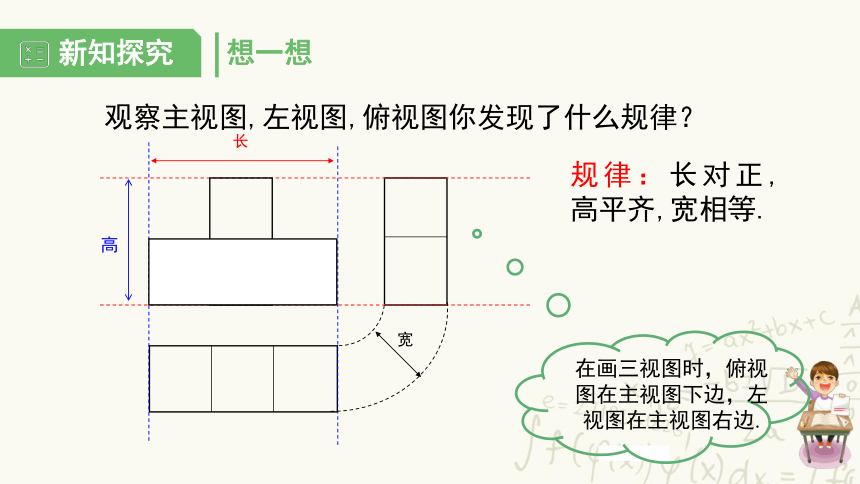
观察主视图,左视图,俯视图你发现了什么规律?
高
长
宽
在画三视图时,俯视图在主视图下边,左视图在主视图右边.
规律:长对正,高平齐,宽相等.
想一想
新知探究
练一练
下面几个几何体中,主视图是圆的是(
)
B
A
B
C
D
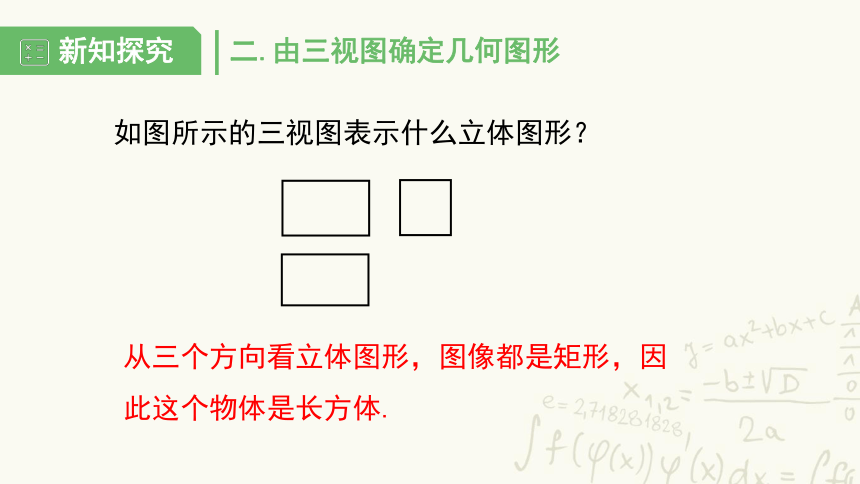
如图所示的三视图表示什么立体图形?
从三个方向看立体图形,图像都是矩形,因此这个物体是长方体.
新知探究
二.由三视图确定几何图形
新知探究
归纳总结
由三视图想象立体图形,要先根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
新知探究
归纳总结
方法点拨:在根据三视图猜想几何体的形状时,要分步进行,先根据比较简单的某一视图猜想可能是哪些几何体;再根据另外两个视图分别猜想可能是哪些几何体,它们的公共部分即为问题的答案.否则,急于求成,眉毛胡子一把抓,则容易出现顾此失彼的错误.
新知探究
练一练
如图是某几何体的三视图,则这个几何体是(
)
A.棱柱
B.圆柱
C.棱锥
D.圆锥
D
俯视图
主视图
左视图
03
典型例题
典型例题
1.长方体的主视图与俯视图如图所示,则这个长方体的体积是(
)
A.52
B.32
C.24
D.9
C
典型例题
2.下列四个几何体中,主视图和俯视图都为矩形的是(
)
B
A
B
C
D
典型例题
3.将一个棱长为1的正方体水平放于桌面上(始终保持正方体的一个面落在桌面上),则该正方体的正视图的面积最大值为(
)
C
A.2
B.
C.
D.1
典型例题
俯视图
主视图
左视图
8cm
4cm
3cm
4.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积和体积。
该几何体的形状是直四棱柱。
棱柱的侧面积=
×4×8=80(cm3)
棱柱的体积=×3×4×8=48(cm3)
典型例题
俯视图
主视图
左视图
8cm
4cm
3cm
解:该几何体的形状是直四棱柱。
由三视图可知,棱柱底面菱形的对角线长分别为4cm和3cm,
∴菱形的边长为cm.
棱柱的侧面积=
×4×8=80(cm3)
棱柱的体积=×3×4×8=48(cm3)
04
拓展提高
拓展提高
1.如图,粗线表示嵌在玻璃正方体内的一根铁丝,请画出该正方体的三视图:
拓展提高
答案:
俯视图
主视图
左视图
拓展提高
2.已知一个几何体的三视图和有关尺寸如图所示,请写出该几何体的名称,并求出它的表面积和体积。
俯视图
主视图
左视图
8cm
6cm
4cm
三棱柱
S表=144cm3
V=96cm3
拓展提高
8cm
4cm
6cm
解:根据三视图可以得出此物体是三棱柱,如图所示。
∴
S表=6×8+4×6+4×8+4×10
=144(cm3)
V=×6×8×4=96(cm3)
05
课堂小结
课堂小结
06
作业布置
1、巩固本章所学,能够熟练并巧妙利用三视图解决问题;
2、完成课本习题
3.3
A、B组.
作业布置
谢
谢
观
看
三视图
教学课件
湘教版九年级下册
01
新课导入
新课导入
这首诗教会了我们怎样观察物体(横看、侧看、近看、身处其中看),这类似于本节课所研究的内容——三视图。
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
——苏轼
02
新知探究
新知探究
视图
从某一角度观察物体在正投影下
的像称为该物体的一个视图
主视图:从正面得到的视图
概念
三视图的组成
左视图:从左面得到的视图
俯视图:从上面得到的视图
三视图的画法
长对正,高平齐,宽相等
看得见的轮廓线画成实线,看
不见的轮廓线画成虚线
为表示球等几何体的对称轴,
可在视图中加画点划线
一.几何体的三视图
新知探究
俯视图
从上面看
从正面看
主视图
从左面看
左视图
新知探究
观察主视图,左视图,俯视图你发现了什么规律?
高
长
宽
在画三视图时,俯视图在主视图下边,左视图在主视图右边.
规律:长对正,高平齐,宽相等.
想一想
新知探究
练一练
下面几个几何体中,主视图是圆的是(
)
B
A
B
C
D
如图所示的三视图表示什么立体图形?
从三个方向看立体图形,图像都是矩形,因此这个物体是长方体.
新知探究
二.由三视图确定几何图形
新知探究
归纳总结
由三视图想象立体图形,要先根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
新知探究
归纳总结
方法点拨:在根据三视图猜想几何体的形状时,要分步进行,先根据比较简单的某一视图猜想可能是哪些几何体;再根据另外两个视图分别猜想可能是哪些几何体,它们的公共部分即为问题的答案.否则,急于求成,眉毛胡子一把抓,则容易出现顾此失彼的错误.
新知探究
练一练
如图是某几何体的三视图,则这个几何体是(
)
A.棱柱
B.圆柱
C.棱锥
D.圆锥
D
俯视图
主视图
左视图
03
典型例题
典型例题
1.长方体的主视图与俯视图如图所示,则这个长方体的体积是(
)
A.52
B.32
C.24
D.9
C
典型例题
2.下列四个几何体中,主视图和俯视图都为矩形的是(
)
B
A
B
C
D
典型例题
3.将一个棱长为1的正方体水平放于桌面上(始终保持正方体的一个面落在桌面上),则该正方体的正视图的面积最大值为(
)
C
A.2
B.
C.
D.1
典型例题
俯视图
主视图
左视图
8cm
4cm
3cm
4.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积和体积。
该几何体的形状是直四棱柱。
棱柱的侧面积=
×4×8=80(cm3)
棱柱的体积=×3×4×8=48(cm3)
典型例题
俯视图
主视图
左视图
8cm
4cm
3cm
解:该几何体的形状是直四棱柱。
由三视图可知,棱柱底面菱形的对角线长分别为4cm和3cm,
∴菱形的边长为cm.
棱柱的侧面积=
×4×8=80(cm3)
棱柱的体积=×3×4×8=48(cm3)
04
拓展提高
拓展提高
1.如图,粗线表示嵌在玻璃正方体内的一根铁丝,请画出该正方体的三视图:
拓展提高
答案:
俯视图
主视图
左视图
拓展提高
2.已知一个几何体的三视图和有关尺寸如图所示,请写出该几何体的名称,并求出它的表面积和体积。
俯视图
主视图
左视图
8cm
6cm
4cm
三棱柱
S表=144cm3
V=96cm3
拓展提高
8cm
4cm
6cm
解:根据三视图可以得出此物体是三棱柱,如图所示。
∴
S表=6×8+4×6+4×8+4×10
=144(cm3)
V=×6×8×4=96(cm3)
05
课堂小结
课堂小结
06
作业布置
1、巩固本章所学,能够熟练并巧妙利用三视图解决问题;
2、完成课本习题
3.3
A、B组.
作业布置
谢
谢
观
看
