湘教版数学九年级下册4.3 用频率估计概率教学课件(共31张PPT)
文档属性
| 名称 | 湘教版数学九年级下册4.3 用频率估计概率教学课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-18 23:01:18 | ||
图片预览










文档简介
(共31张PPT)
用频率估计概率
教学课件
湘教版九年级下册
01
新课导入
新课导入
在现实生活中有些事件发生的结果不是有限个,或各种可能的结果发生的可能性不相等时,怎样求概率?比如说姚明投一个球进球的概率比一般人投一个球进球的概率要大得多,但怎么求姚明投一个进球的概率呢?学完本节知识你就会找到一种好办法.
02
新知探究
新知探究
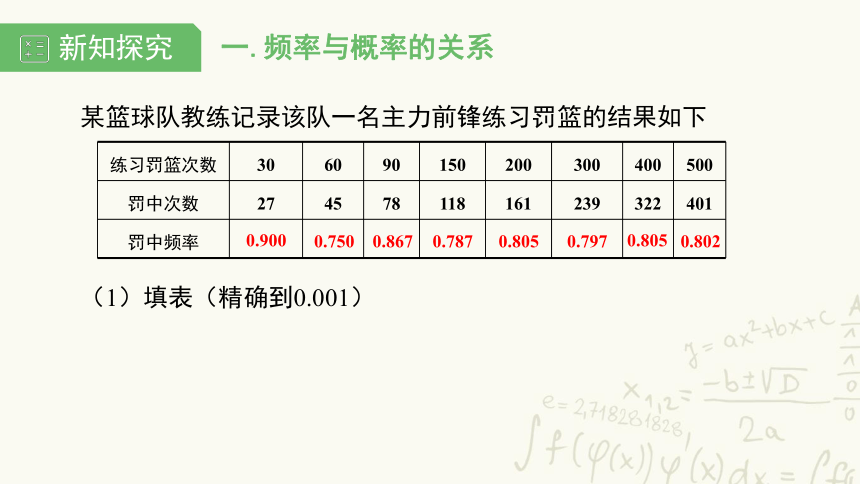
某篮球队教练记录该队一名主力前锋练习罚篮的结果如下
(1)填表(精确到0.001)
练习罚篮次数
30
60
90
150
200
300
400
500
罚中次数
27
45
78
118
161
239
322
401
罚中频率
0.900
0.750
0.867
0.787
0.805
0.797
0.805
0.802
一.频率与概率的关系
新知探究
(2)根据上表的数据,在下图中画统计图表示“罚中频率”
一.频率与概率的关系
新知探究
解:从表中的数据可以发现,随着练习次数的增加,该前锋罚篮命中的频率稳定在0.8左右,所以估计他这次能罚中的概率约为0.8.
(3)比赛中该前锋队员上篮得分并造成对手犯规,罚篮一次,你能估计这次他能罚中的概率是多少吗?
一.频率与概率的关系
新知探究
归纳总结
通过大量重复试验,可以用随机事件发生的频率来估计该事件发生的概率.
新知探究
归纳总结
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,常常是通过统计频率来估计概率,即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生的概率.
新知探究
归纳总结
频率与概率都是随机事件可能性大小的定量刻画,但频率与试验次数有关,因此频率具有随机性;而概率是刻画随机事件发生可能性大小的数值,是一个固定的量,不具有随机性.
新知探究
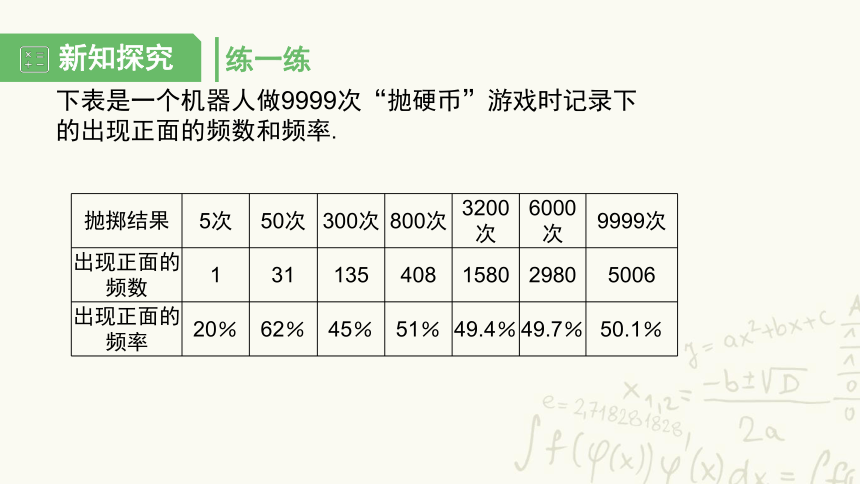
下表是一个机器人做9999次“抛硬币”游戏时记录下的出现正面的频数和频率.
抛掷结果
5次
50次
300次
800次
3200次
6000次
9999次
出现正面的频数
1
31
135
408
1580
2980
5006
出现正面的频率
20%
62%
45%
51%
49.4%
49.7%
50.1%
练一练
新知探究
(1)由这张频数和频率表可知,机器人抛掷完5次时,得到1次正面,正面出现的频率是20%,那么,也就是说机器人抛掷完5次后,得到______次反面,反面出现的频率是______;
(2)由这张频数和频率表可知,机器人抛掷完9999次时,得到______次正面,正面出现的频率是______;那么,也就是说机器人抛掷完9999次时,得到______次反面,反面出现的频率是______;
(3)请你估计一下,抛这枚硬币,正面出现的概率是______.
4
80%
5006
50.1%
4993
49.9%
50%
练一练
新知探究
归纳总结
用频率估计概率时,试验次数越多,频率越接近于概率.
新知探究
二.用频率估计概率
某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球试验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球的次数为6000次.
(1)估计从袋中任意摸出一个球恰好是红球的概率是多少;
(2)请你估计袋中的红球接近多少个.
新知探究
二.用频率估计概率
思路导引:
1.试验总次数为______次,则摸到红球的频率为_________.
2.设红球有x个,根据红球的概率列出方程求解.
8000
0.75
解:
(1)∵20×400=8000,
∴摸到红球的频率为=0.75.
∵试验次数很大,大量试验时,频率接近于概率,
∴估计从袋中任意摸出一个球,恰好是红球的概率是0.75.
(2)设袋中红球有x个,根据题意得=0.75,
解得x=15,
经检验x=15是原分式方程的解.
∴估计袋中的红球接近15个.
新知探究
归纳总结
用频率估计概率的关键:
(1)大量重复试验时,频率可看成概率的近似值;
(2)运用方程思想,根据概率公式列出方程求解.
03
典型例题
典型例题
1.在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其试验次数分别为10次、50次、100次、200次,其中试验相对科学的是(
)
A.甲组
B.乙组
C.丙组
D.丁组
D
典型例题
2.一个不透明的盒子里有n个除颜色之外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子.通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为(
)
A.20
B.24
C.28
D.30
D
典型例题
3.下列随机事件的概率,既可以用列举法求得,又可以用频率估计获得的是(
)
A.
某种幼苗在一定条件下的移植成活率
B.某种柑橘在某次运输过程中的损坏率
C.某射击运动员在某种条件下射出9环以上的概率
D.投掷一枚均匀的骰子,朝上一面为偶数的概率
D
典型例题
4.为估计某一池塘中鱼的总数目,小英将100尾做了标记的鱼投入池塘中,几天后,随机捕捞,每次捕捞后做好记录,然后将鱼放回,如此进行20次,记录数据如下:
总条数
50
45
60
48
10
30
42
38
15
10
标记数
2
1
3
2
0
1
1
2
0
1
总条数
53
36
27
34
43
26
18
22
25
47
标记数
2
1
2
1
2
1
1
2
1
2
典型例题
(1)估计池塘中鱼的总数,根据这种方法估算是否准确?
(19+2
=.
尾.
此数据相对准确,试验的次数越多,越接近于准确数.
解:
典型例题
(2)请设计另一种标记的方法,使得估计更加精准.
先从鱼塘中捕捞50条鱼,称他们的质量,做好记号再放回去,过几天又捕捞了100条鱼,称他们的质量,设鱼塘中鱼的总质量为,利用条数和质量的比组成方程组解决问题即可.
04
拓展提高
拓展提高
为获取某自然保护区内某种野生动物的数量,工作人员逮到该种动物1200只,做标记后放回.若干天后,再逮到该种动物1000只,其中有100只做过标记。按概率方法估算,保护区内这种动物有多少只?
12000只
拓展提高
解:∵该种动物1000只中有100只做过标记,
∴做过标记的动物占这种动物总数的=
∵该种动物共1200只做了标记,
∴保护区内这种动物有1200÷=12000(只).
05
课堂小结
课堂小结
06
作业布置
1、巩固本章所学,仔细理解统计的实际意义
2、完成课本习题
4.3
A、B组以及复习题4
作业布置
谢
谢
观
看
用频率估计概率
教学课件
湘教版九年级下册
01
新课导入
新课导入
在现实生活中有些事件发生的结果不是有限个,或各种可能的结果发生的可能性不相等时,怎样求概率?比如说姚明投一个球进球的概率比一般人投一个球进球的概率要大得多,但怎么求姚明投一个进球的概率呢?学完本节知识你就会找到一种好办法.
02
新知探究
新知探究
某篮球队教练记录该队一名主力前锋练习罚篮的结果如下
(1)填表(精确到0.001)
练习罚篮次数
30
60
90
150
200
300
400
500
罚中次数
27
45
78
118
161
239
322
401
罚中频率
0.900
0.750
0.867
0.787
0.805
0.797
0.805
0.802
一.频率与概率的关系
新知探究
(2)根据上表的数据,在下图中画统计图表示“罚中频率”
一.频率与概率的关系
新知探究
解:从表中的数据可以发现,随着练习次数的增加,该前锋罚篮命中的频率稳定在0.8左右,所以估计他这次能罚中的概率约为0.8.
(3)比赛中该前锋队员上篮得分并造成对手犯规,罚篮一次,你能估计这次他能罚中的概率是多少吗?
一.频率与概率的关系
新知探究
归纳总结
通过大量重复试验,可以用随机事件发生的频率来估计该事件发生的概率.
新知探究
归纳总结
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,常常是通过统计频率来估计概率,即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生的概率.
新知探究
归纳总结
频率与概率都是随机事件可能性大小的定量刻画,但频率与试验次数有关,因此频率具有随机性;而概率是刻画随机事件发生可能性大小的数值,是一个固定的量,不具有随机性.
新知探究
下表是一个机器人做9999次“抛硬币”游戏时记录下的出现正面的频数和频率.
抛掷结果
5次
50次
300次
800次
3200次
6000次
9999次
出现正面的频数
1
31
135
408
1580
2980
5006
出现正面的频率
20%
62%
45%
51%
49.4%
49.7%
50.1%
练一练
新知探究
(1)由这张频数和频率表可知,机器人抛掷完5次时,得到1次正面,正面出现的频率是20%,那么,也就是说机器人抛掷完5次后,得到______次反面,反面出现的频率是______;
(2)由这张频数和频率表可知,机器人抛掷完9999次时,得到______次正面,正面出现的频率是______;那么,也就是说机器人抛掷完9999次时,得到______次反面,反面出现的频率是______;
(3)请你估计一下,抛这枚硬币,正面出现的概率是______.
4
80%
5006
50.1%
4993
49.9%
50%
练一练
新知探究
归纳总结
用频率估计概率时,试验次数越多,频率越接近于概率.
新知探究
二.用频率估计概率
某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球试验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球的次数为6000次.
(1)估计从袋中任意摸出一个球恰好是红球的概率是多少;
(2)请你估计袋中的红球接近多少个.
新知探究
二.用频率估计概率
思路导引:
1.试验总次数为______次,则摸到红球的频率为_________.
2.设红球有x个,根据红球的概率列出方程求解.
8000
0.75
解:
(1)∵20×400=8000,
∴摸到红球的频率为=0.75.
∵试验次数很大,大量试验时,频率接近于概率,
∴估计从袋中任意摸出一个球,恰好是红球的概率是0.75.
(2)设袋中红球有x个,根据题意得=0.75,
解得x=15,
经检验x=15是原分式方程的解.
∴估计袋中的红球接近15个.
新知探究
归纳总结
用频率估计概率的关键:
(1)大量重复试验时,频率可看成概率的近似值;
(2)运用方程思想,根据概率公式列出方程求解.
03
典型例题
典型例题
1.在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其试验次数分别为10次、50次、100次、200次,其中试验相对科学的是(
)
A.甲组
B.乙组
C.丙组
D.丁组
D
典型例题
2.一个不透明的盒子里有n个除颜色之外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子.通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为(
)
A.20
B.24
C.28
D.30
D
典型例题
3.下列随机事件的概率,既可以用列举法求得,又可以用频率估计获得的是(
)
A.
某种幼苗在一定条件下的移植成活率
B.某种柑橘在某次运输过程中的损坏率
C.某射击运动员在某种条件下射出9环以上的概率
D.投掷一枚均匀的骰子,朝上一面为偶数的概率
D
典型例题
4.为估计某一池塘中鱼的总数目,小英将100尾做了标记的鱼投入池塘中,几天后,随机捕捞,每次捕捞后做好记录,然后将鱼放回,如此进行20次,记录数据如下:
总条数
50
45
60
48
10
30
42
38
15
10
标记数
2
1
3
2
0
1
1
2
0
1
总条数
53
36
27
34
43
26
18
22
25
47
标记数
2
1
2
1
2
1
1
2
1
2
典型例题
(1)估计池塘中鱼的总数,根据这种方法估算是否准确?
(19+2
=.
尾.
此数据相对准确,试验的次数越多,越接近于准确数.
解:
典型例题
(2)请设计另一种标记的方法,使得估计更加精准.
先从鱼塘中捕捞50条鱼,称他们的质量,做好记号再放回去,过几天又捕捞了100条鱼,称他们的质量,设鱼塘中鱼的总质量为,利用条数和质量的比组成方程组解决问题即可.
04
拓展提高
拓展提高
为获取某自然保护区内某种野生动物的数量,工作人员逮到该种动物1200只,做标记后放回.若干天后,再逮到该种动物1000只,其中有100只做过标记。按概率方法估算,保护区内这种动物有多少只?
12000只
拓展提高
解:∵该种动物1000只中有100只做过标记,
∴做过标记的动物占这种动物总数的=
∵该种动物共1200只做了标记,
∴保护区内这种动物有1200÷=12000(只).
05
课堂小结
课堂小结
06
作业布置
1、巩固本章所学,仔细理解统计的实际意义
2、完成课本习题
4.3
A、B组以及复习题4
作业布置
谢
谢
观
看
