高中数学高二第一学期8.3平面向量的分解定理_导学案2-沪教版
文档属性
| 名称 | 高中数学高二第一学期8.3平面向量的分解定理_导学案2-沪教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 74.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 1970-01-01 08:00:00 | ||
图片预览

文档简介
平面向量的分解定理
【学习目标】
1.理解平面向量的分解定理,掌握平面内任一向量都可以用两个不平行的向量来表示。
2.掌握基的概念,并会用一组基底向量表示平面内的一些简单的向量。
3.经历平面向量分解定理的探索过程,培养观察能力、抽象概括能力。
【学习重难点】
重点:
平面向量分解定理的应用。
难点:
平面向量分解定理的探索过程。
【学习过程】
一、自主学习
36162654523836a
e1
e2
00a
e1
e2
知识迁移:(1)速度的分解;(2)力的分解;
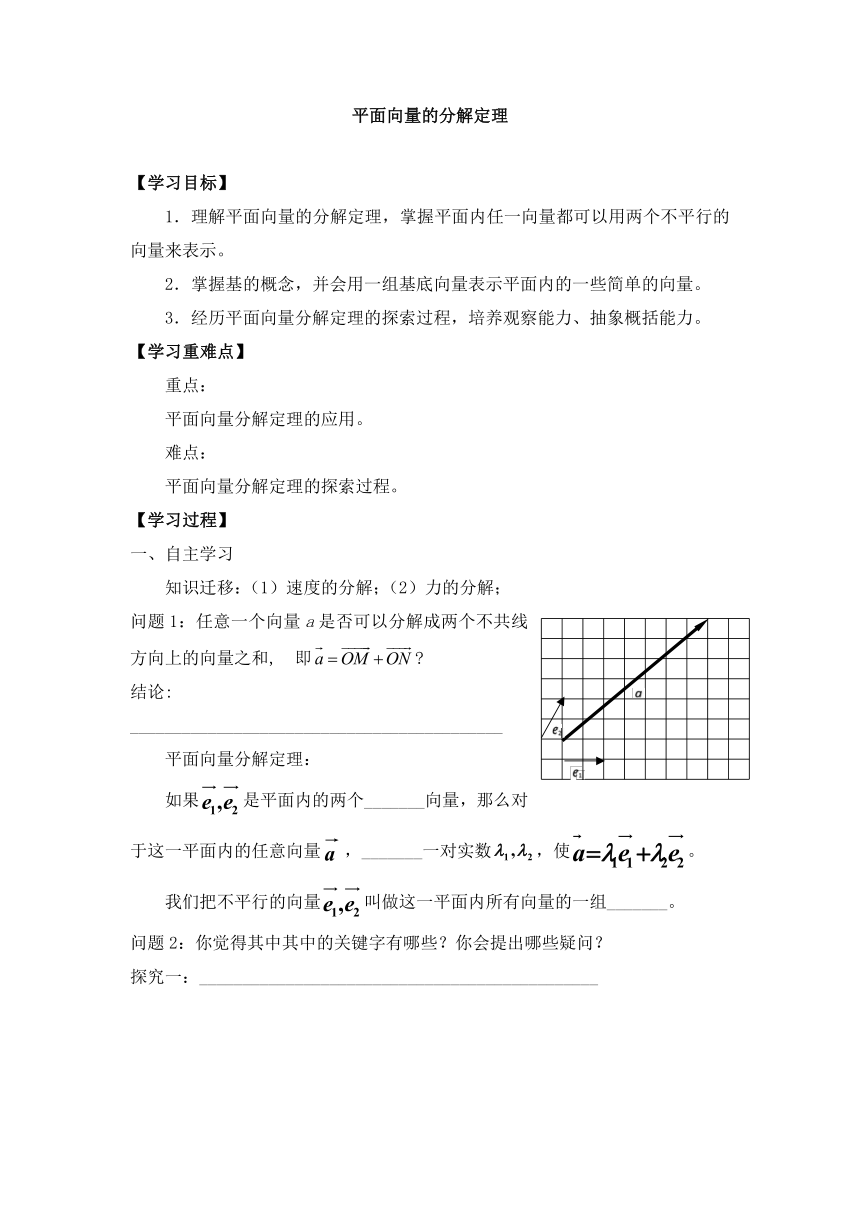
问题1:任意一个向量a是否可以分解成两个不共线方向上的向量之和, 即?
结论:
___________________________________________
平面向量分解定理:
如果是平面内的两个_______向量,那么对于这一平面内的任意向量,_______一对实数,使。
我们把不平行的向量叫做这一平面内所有向量的一组_______。
问题2:你觉得其中其中的关键字有哪些?你会提出哪些疑问?
探究一:______________________________________________
结论:_________________________________________________
探究二:_______________________________________________
二、例题分析
3426676207034例1. 如图所示,的对角线AC和BD交于点M,
,试用基底表示
350972967286O
B
C
A
00O
B
C
A
例2.(1)已知,用表示;
(2)如图,在中,C为直线AB上一点,
。
求证:
38138100O
B
C
A
00O
B
C
A
反思:结论可以看做是吗?
变式:如果存在实数,使,
求证:A,B,C三点共线。
结论:
___________________________________________________________________________。
【学习目标】
1.理解平面向量的分解定理,掌握平面内任一向量都可以用两个不平行的向量来表示。
2.掌握基的概念,并会用一组基底向量表示平面内的一些简单的向量。
3.经历平面向量分解定理的探索过程,培养观察能力、抽象概括能力。
【学习重难点】
重点:
平面向量分解定理的应用。
难点:
平面向量分解定理的探索过程。
【学习过程】
一、自主学习
36162654523836a
e1
e2
00a
e1
e2
知识迁移:(1)速度的分解;(2)力的分解;
问题1:任意一个向量a是否可以分解成两个不共线方向上的向量之和, 即?
结论:
___________________________________________
平面向量分解定理:
如果是平面内的两个_______向量,那么对于这一平面内的任意向量,_______一对实数,使。
我们把不平行的向量叫做这一平面内所有向量的一组_______。
问题2:你觉得其中其中的关键字有哪些?你会提出哪些疑问?
探究一:______________________________________________
结论:_________________________________________________
探究二:_______________________________________________
二、例题分析
3426676207034例1. 如图所示,的对角线AC和BD交于点M,
,试用基底表示
350972967286O
B
C
A
00O
B
C
A
例2.(1)已知,用表示;
(2)如图,在中,C为直线AB上一点,
。
求证:
38138100O
B
C
A
00O
B
C
A
反思:结论可以看做是吗?
变式:如果存在实数,使,
求证:A,B,C三点共线。
结论:
___________________________________________________________________________。
