高中数学高三第一学期14.3空间直线与平面的位置关系_导学案1-沪教版
文档属性
| 名称 | 高中数学高三第一学期14.3空间直线与平面的位置关系_导学案1-沪教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 1970-01-01 08:00:00 | ||
图片预览

文档简介
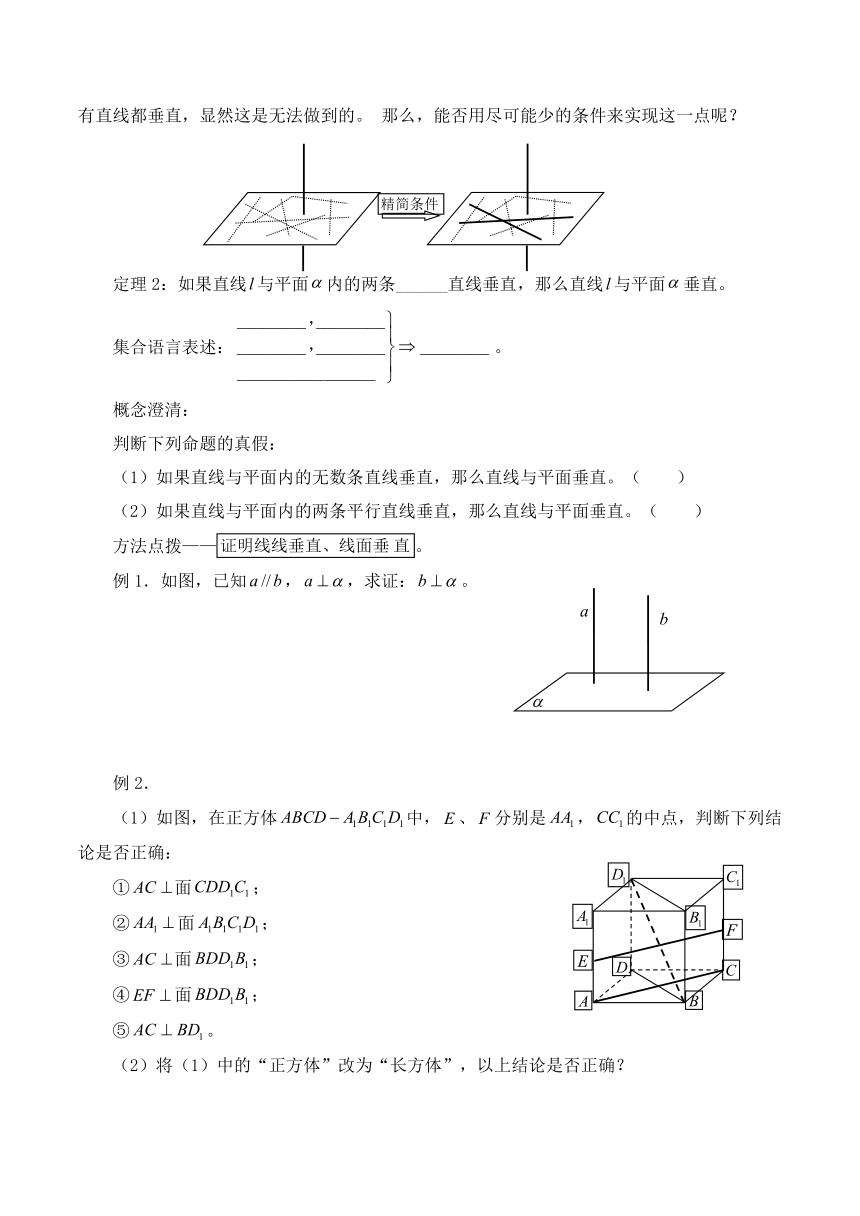
空间直线与平面的位置关系
【学习目标】
1.理解空间直线和平面垂直的定义、定理。
2.掌握线线垂直、线面垂直的证明方法。
【学习重难点】
1.理解空间中各种“距离”的定义。
2.掌握空间距离的确定与计算方法。
【学习过程】
一、情景引入
简述下列问题的结论,并画图说明:
(1)直线平面,直线,则和的位置关系如何?
(2)直线平面,直线,则和的位置关系如何?
归纳总结:
空间中直线与平面的位置关系。
二、学习新课
1.直线与平面垂直:
定义:如果直线与平面内的_________直线都垂直,就说直线与平面垂直,记做__________。
根据定义,为了证明一条直线与一个平面垂直,我们必须验证这条直线与这个平面内的所有直线都垂直,显然这是无法做到的。 那么,能否用尽可能少的条件来实现这一点呢?
定理2:如果直线与平面内的两条______直线垂直,那么直线与平面垂直。
集合语言表述:。
概念澄清:
判断下列命题的真假:
(1)如果直线与平面内的无数条直线垂直,那么直线与平面垂直。( )
(2)如果直线与平面内的两条平行直线垂直,那么直线与平面垂直。( )
方法点拨——。
例1.如图,已知,,求证:。
例2.
(1)如图,在正方体中,、分别是,的中点,判断下列结论是否正确:
①面;
②面;
③面;
④面;
⑤。
(2)将(1)中的“正方体”改为“长方体”,以上结论是否正确?
例3.继续研究例2的正方体,、分别是,的中点,求证:。
说明:根据定理2 ,要证明线线垂直,可找线面垂直,反之亦然。即:
。
这里体现了高中数学的转化与化归思想。
练习:点是平行四边形所在平面外一点,是对角线与的交点,且,。 求证:平面。
2.空间中的各种“距离”。
(1)点和平面的距离:设点是平面外一点,过作平面的垂线,垂足为,把________________叫做点和平面的距离;
(2)直线和平面的距离:设直线平面,在直线上任取一点,把________________的距离叫做直线和平面的距离;
(3)平面和平面的距离:设平面平行于平面,在平面上任取一点,把________________的距离叫做平面和平面的距离;
(4)异面直线的公垂线和距离:设直线与直线是异面直线,当,且,,把直线叫做异面直线、的公垂线,________________叫做异面直线和的距离。
方法点拨——。
例4.如图,已知长方体的棱长、和的长分别为、和。
(1)求点和点的距离;
(2)求点到棱的距离;
(3)求棱和平面的距离;
(4)求异面直线和的距离。
练习:已知长方体的棱,,。
(1)点和点的距离是_____________;
(2)点和直线的距离是_____________;
(3)直线和平面的距离是_____________;
(4)直线和的距离是_____________。
三、小结
1.直线与直线垂直、直线与平面垂直的证明;
2.空间中各种“距离”的确定与计算。
【学习目标】
1.理解空间直线和平面垂直的定义、定理。
2.掌握线线垂直、线面垂直的证明方法。
【学习重难点】
1.理解空间中各种“距离”的定义。
2.掌握空间距离的确定与计算方法。
【学习过程】
一、情景引入
简述下列问题的结论,并画图说明:
(1)直线平面,直线,则和的位置关系如何?
(2)直线平面,直线,则和的位置关系如何?
归纳总结:
空间中直线与平面的位置关系。
二、学习新课
1.直线与平面垂直:
定义:如果直线与平面内的_________直线都垂直,就说直线与平面垂直,记做__________。
根据定义,为了证明一条直线与一个平面垂直,我们必须验证这条直线与这个平面内的所有直线都垂直,显然这是无法做到的。 那么,能否用尽可能少的条件来实现这一点呢?
定理2:如果直线与平面内的两条______直线垂直,那么直线与平面垂直。
集合语言表述:。
概念澄清:
判断下列命题的真假:
(1)如果直线与平面内的无数条直线垂直,那么直线与平面垂直。( )
(2)如果直线与平面内的两条平行直线垂直,那么直线与平面垂直。( )
方法点拨——。
例1.如图,已知,,求证:。
例2.
(1)如图,在正方体中,、分别是,的中点,判断下列结论是否正确:
①面;
②面;
③面;
④面;
⑤。
(2)将(1)中的“正方体”改为“长方体”,以上结论是否正确?
例3.继续研究例2的正方体,、分别是,的中点,求证:。
说明:根据定理2 ,要证明线线垂直,可找线面垂直,反之亦然。即:
。
这里体现了高中数学的转化与化归思想。
练习:点是平行四边形所在平面外一点,是对角线与的交点,且,。 求证:平面。
2.空间中的各种“距离”。
(1)点和平面的距离:设点是平面外一点,过作平面的垂线,垂足为,把________________叫做点和平面的距离;
(2)直线和平面的距离:设直线平面,在直线上任取一点,把________________的距离叫做直线和平面的距离;
(3)平面和平面的距离:设平面平行于平面,在平面上任取一点,把________________的距离叫做平面和平面的距离;
(4)异面直线的公垂线和距离:设直线与直线是异面直线,当,且,,把直线叫做异面直线、的公垂线,________________叫做异面直线和的距离。
方法点拨——。
例4.如图,已知长方体的棱长、和的长分别为、和。
(1)求点和点的距离;
(2)求点到棱的距离;
(3)求棱和平面的距离;
(4)求异面直线和的距离。
练习:已知长方体的棱,,。
(1)点和点的距离是_____________;
(2)点和直线的距离是_____________;
(3)直线和平面的距离是_____________;
(4)直线和的距离是_____________。
三、小结
1.直线与直线垂直、直线与平面垂直的证明;
2.空间中各种“距离”的确定与计算。
