高中数学高三第一学期15.3旋转体的概念_导学案1-沪教版
文档属性
| 名称 | 高中数学高三第一学期15.3旋转体的概念_导学案1-沪教版 |  | |
| 格式 | doc | ||
| 文件大小 | 53.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 1970-01-01 08:00:00 | ||
图片预览

文档简介
旋转体的概念
【学习目标】
1.会用语言概述球、圆柱、圆锥的结构特征。
2.能根据几何结构特征对空间物体进行分类。
3.提高学生的观察能力;培养学生的空间想象能力和抽象括能力。
【学习重难点】
重点:
让学生感受大量空间实物及模型、概括出柱、锥、球的结构特征。
难点:
柱、锥、球的结构特征的概括。
【学习过程】
一、预习内容
1.旋转面、旋转体的概念:
一条_____________绕它所在平面内的一条________________所形成的曲面称为旋转面;
_____________的旋转面围成的几何体称为旋转体。__________________________叫旋转体的轴。
2.球:以半圆的_______________为旋转轴,将半圆旋转所形成的曲面叫________,_______所围成的几何体叫做________,半圆的圆心叫________,连接_________________上任意一点的线段叫做________。
3.圆柱、圆锥:分别以矩形的一边,直角三角形的一条直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体,分别叫做________、________。
旋转轴称为它们的_____,在轴上这条边的长度称为它们的_____。垂直于轴的边旋转而成的圆面称为它们的________,平行于轴的边旋转而成的曲面称为它们的________,平行于轴的边在旋转中的任何位置称为侧面的________。
圆柱、圆锥都是_______________。
二、探究
(一)研探新知。
1.球:
(1)表示:球用___________________表示;
如图中球表示为__________。
截面:
用一个平面去截一个球,截面是_______。
设球的半径为R,截面圆半径为r,球心与截面圆圆心的距离为d,则R、r、d三者之间的关系是__________________________。
2.圆柱:
(1)表示:
圆柱用____________________表示;
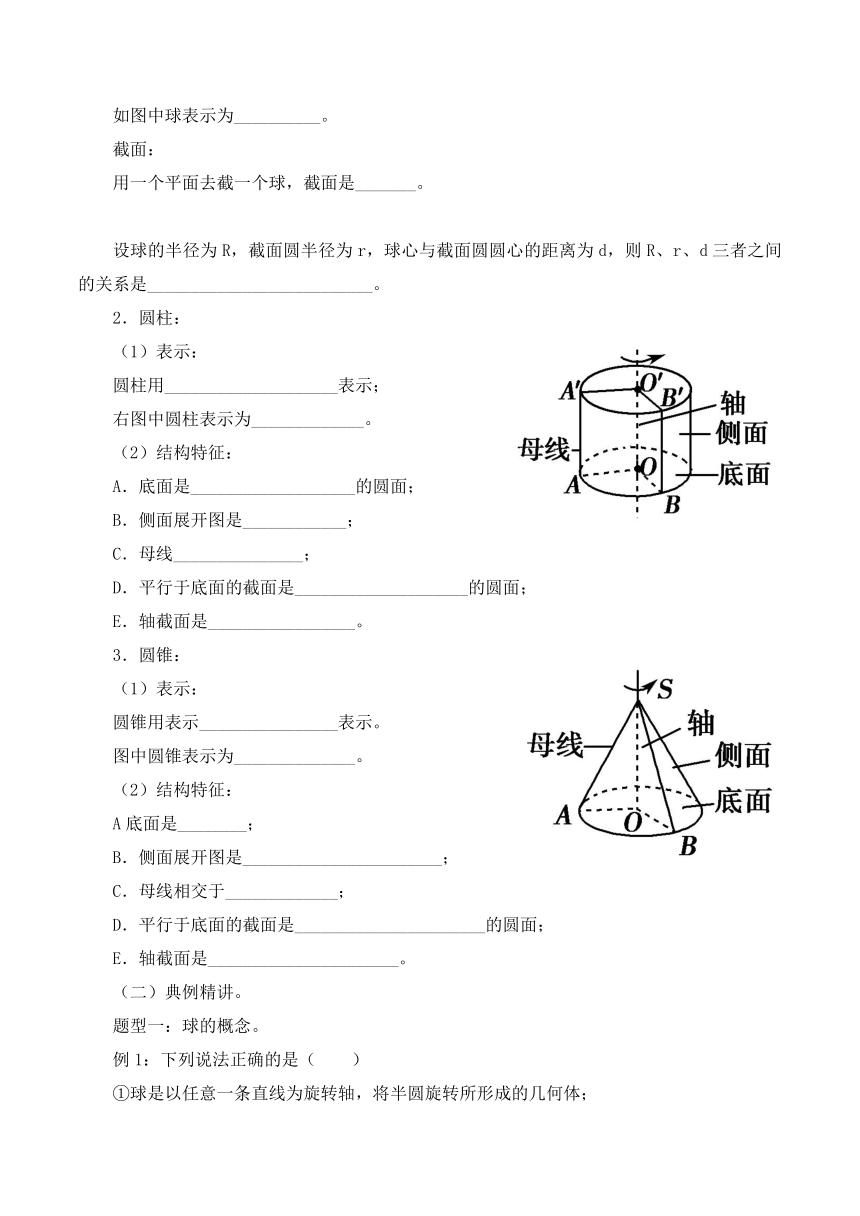
右图中圆柱表示为_____________。
(2)结构特征:
A.底面是___________________的圆面;
B.侧面展开图是____________;
C.母线_______________;
D.平行于底面的截面是____________________的圆面;
E.轴截面是_________________。
3.圆锥:
(1)表示:
圆锥用表示________________表示。
图中圆锥表示为______________。
(2)结构特征:
A底面是________;
B.侧面展开图是_______________________;
C.母线相交于_____________;
D.平行于底面的截面是______________________的圆面;
E.轴截面是______________________。
(二)典例精讲。
题型一:球的概念。
例1:下列说法正确的是( )
①球是以任意一条直线为旋转轴,将半圆旋转所形成的几何体;
②用任一平面去截球,截面是一个圆;
③过球的球心做球的截面,所得截面的半径与球的半径相等。
A.①;
B.②;
C.③;
D.②③。
规律技巧:掌握球的概念是解决此类问题的关键。
变式训练1:
球的半径有________条,直径有________条,用任意平面截球,截面为________。
题型二:圆柱与圆锥的概念。
例2:下列叙述中正确的个数是( )
①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;
②以直角梯形的一腰为轴旋转一周所得的旋转体是圆柱;
③圆柱、圆锥的底面都是圆;
④用一个平面去截圆锥,得到一个圆锥。
A.0;
B.1;
C.2;
D.3。
规律技巧:掌握圆柱、圆锥的概念及特征是解决此类问题的关键。
题型三:简单几何体的综合运用。
例4.已知ABCD为正方形,分别以AB,AC所在的直线为旋转轴,将正方形绕旋转轴所在的直线旋转一周,判断所形成的几何体的形状。
点拨:对于该题可从旋转的方法加以分析。
解析:
规律技巧:平面图形旋转时旋转轴不同旋转所得到的几何体也不同。
变式训练5.在直角三角形中,以其斜边所在直线为轴旋转一周所得的旋转体是( )
A.圆锥;
B.圆柱;
C.圆台;
D.以上都不对。
三、课时小结
球,圆柱,圆锥是简单的旋转体,它们是日常生活中常见的几何体。
【学习目标】
1.会用语言概述球、圆柱、圆锥的结构特征。
2.能根据几何结构特征对空间物体进行分类。
3.提高学生的观察能力;培养学生的空间想象能力和抽象括能力。
【学习重难点】
重点:
让学生感受大量空间实物及模型、概括出柱、锥、球的结构特征。
难点:
柱、锥、球的结构特征的概括。
【学习过程】
一、预习内容
1.旋转面、旋转体的概念:
一条_____________绕它所在平面内的一条________________所形成的曲面称为旋转面;
_____________的旋转面围成的几何体称为旋转体。__________________________叫旋转体的轴。
2.球:以半圆的_______________为旋转轴,将半圆旋转所形成的曲面叫________,_______所围成的几何体叫做________,半圆的圆心叫________,连接_________________上任意一点的线段叫做________。
3.圆柱、圆锥:分别以矩形的一边,直角三角形的一条直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体,分别叫做________、________。
旋转轴称为它们的_____,在轴上这条边的长度称为它们的_____。垂直于轴的边旋转而成的圆面称为它们的________,平行于轴的边旋转而成的曲面称为它们的________,平行于轴的边在旋转中的任何位置称为侧面的________。
圆柱、圆锥都是_______________。
二、探究
(一)研探新知。
1.球:
(1)表示:球用___________________表示;
如图中球表示为__________。
截面:
用一个平面去截一个球,截面是_______。
设球的半径为R,截面圆半径为r,球心与截面圆圆心的距离为d,则R、r、d三者之间的关系是__________________________。
2.圆柱:
(1)表示:
圆柱用____________________表示;
右图中圆柱表示为_____________。
(2)结构特征:
A.底面是___________________的圆面;
B.侧面展开图是____________;
C.母线_______________;
D.平行于底面的截面是____________________的圆面;
E.轴截面是_________________。
3.圆锥:
(1)表示:
圆锥用表示________________表示。
图中圆锥表示为______________。
(2)结构特征:
A底面是________;
B.侧面展开图是_______________________;
C.母线相交于_____________;
D.平行于底面的截面是______________________的圆面;
E.轴截面是______________________。
(二)典例精讲。
题型一:球的概念。
例1:下列说法正确的是( )
①球是以任意一条直线为旋转轴,将半圆旋转所形成的几何体;
②用任一平面去截球,截面是一个圆;
③过球的球心做球的截面,所得截面的半径与球的半径相等。
A.①;
B.②;
C.③;
D.②③。
规律技巧:掌握球的概念是解决此类问题的关键。
变式训练1:
球的半径有________条,直径有________条,用任意平面截球,截面为________。
题型二:圆柱与圆锥的概念。
例2:下列叙述中正确的个数是( )
①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;
②以直角梯形的一腰为轴旋转一周所得的旋转体是圆柱;
③圆柱、圆锥的底面都是圆;
④用一个平面去截圆锥,得到一个圆锥。
A.0;
B.1;
C.2;
D.3。
规律技巧:掌握圆柱、圆锥的概念及特征是解决此类问题的关键。
题型三:简单几何体的综合运用。
例4.已知ABCD为正方形,分别以AB,AC所在的直线为旋转轴,将正方形绕旋转轴所在的直线旋转一周,判断所形成的几何体的形状。
点拨:对于该题可从旋转的方法加以分析。
解析:
规律技巧:平面图形旋转时旋转轴不同旋转所得到的几何体也不同。
变式训练5.在直角三角形中,以其斜边所在直线为轴旋转一周所得的旋转体是( )
A.圆锥;
B.圆柱;
C.圆台;
D.以上都不对。
三、课时小结
球,圆柱,圆锥是简单的旋转体,它们是日常生活中常见的几何体。
