人教版八年级上册 数学 12.3 角的平分线的性质课件(21张PPT)
文档属性
| 名称 | 人教版八年级上册 数学 12.3 角的平分线的性质课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 264.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 16:38:11 | ||
图片预览





文档简介
12.3 角的平分线的性质
[教学内容1]
生活中有很多数学问题:
小明家居住在通州区一栋居民楼的一楼,刚好位于一条暖气和天然气管道所成角的平分线上的P点,要从P点建两条管道,分别与暖气管道和天然气管道相连.
问题1:怎样修建管道最短?
问题2:新修的两条管道长度有什么关系?.
.
P
暖气
天然气
创设情境
问题1 给你一个角,怎样得到这个角的
平分线?
追问1 你能评价这些方法吗?在生产生活中,这
些方法是否可行呢?
感悟实践经验,用尺规作角的平分线
用量角器度量,也可用折纸的方法.
感悟实践经验,用尺规作角的平分线
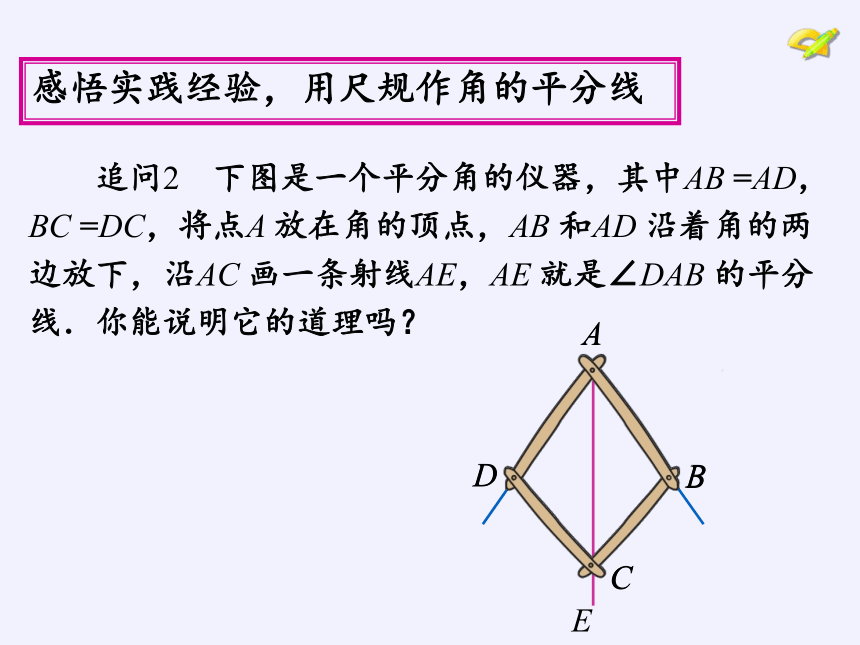
追问2 下图是一个平分角的仪器,其中AB =AD,
BC =DC,将点A 放在角的顶点,AB 和AD 沿着角的两
边放下,沿AC 画一条射线AE,AE 就是∠DAB 的平分
线.你能说明它的道理吗?
A
B
D
C
E
A
B
D
C
感悟实践经验,用尺规作角的平分线
追问3 从利用平分角的仪器画角的平分线中,你
受到哪些启发?如何利用直尺和圆规作一个角的平分线?
感悟实践经验,用尺规作角的平分线
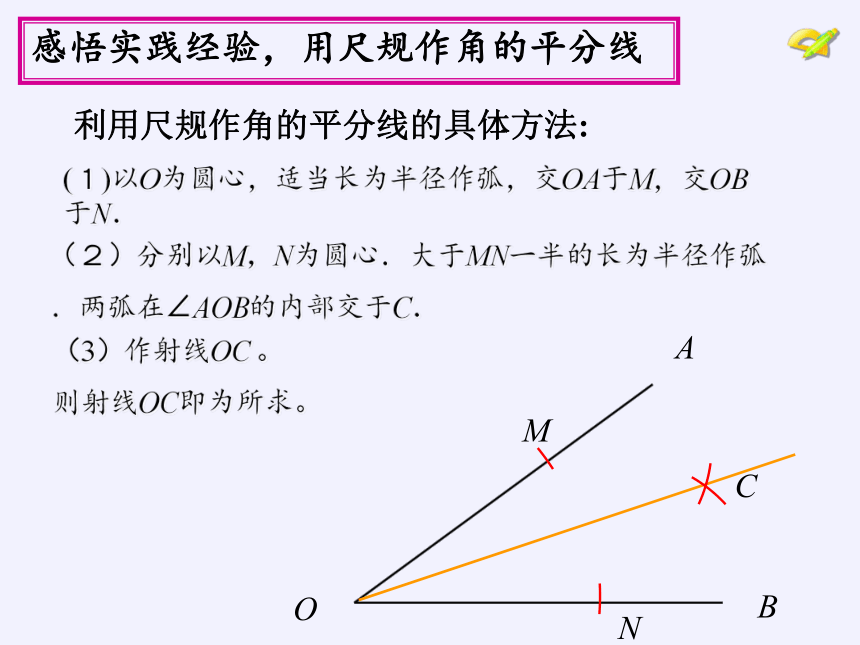
利用尺规作角的平分线的具体方法:
A
B
O
M
N
C
(2)分别以M,N为圆心.大于MN一半的长为半径作弧.两弧在∠AOB的内部交于C.
(3)作射线OC 。
则射线OC即为所求。
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
感悟实践经验,用尺规作角的平分线
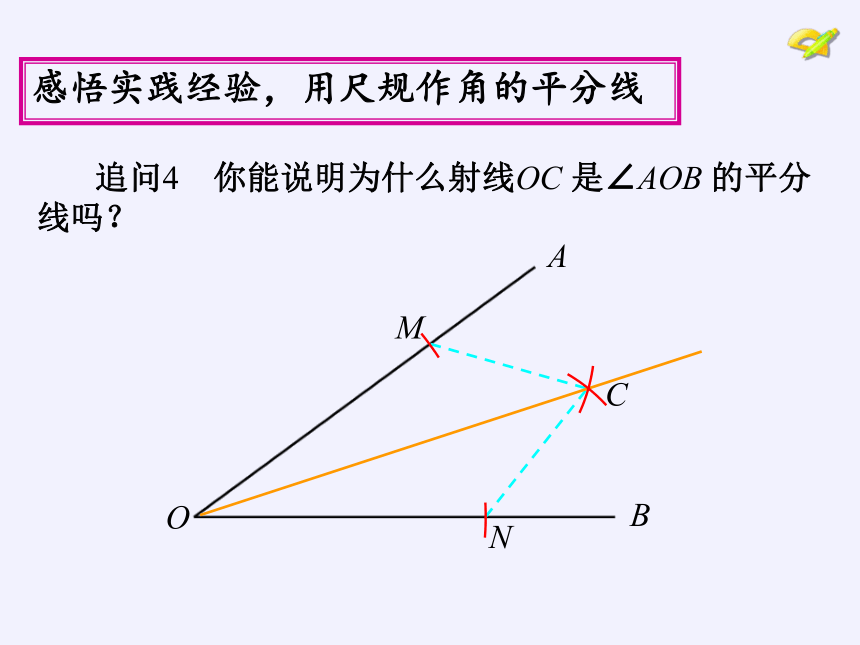
追问4 你能说明为什么射线OC 是∠AOB 的平分线吗?
A
B
O
M
N
C
经历实验过程,发现并证明角的平分线的性质
如图,任意作一个角∠AOB,作出∠AOB的平分线
OC,在OC 上任取一点P,过点
P 画出OA,OB 的垂线,分别记
垂足为D,E,测量 PD,PE 并
作比较,你得到什么结论?
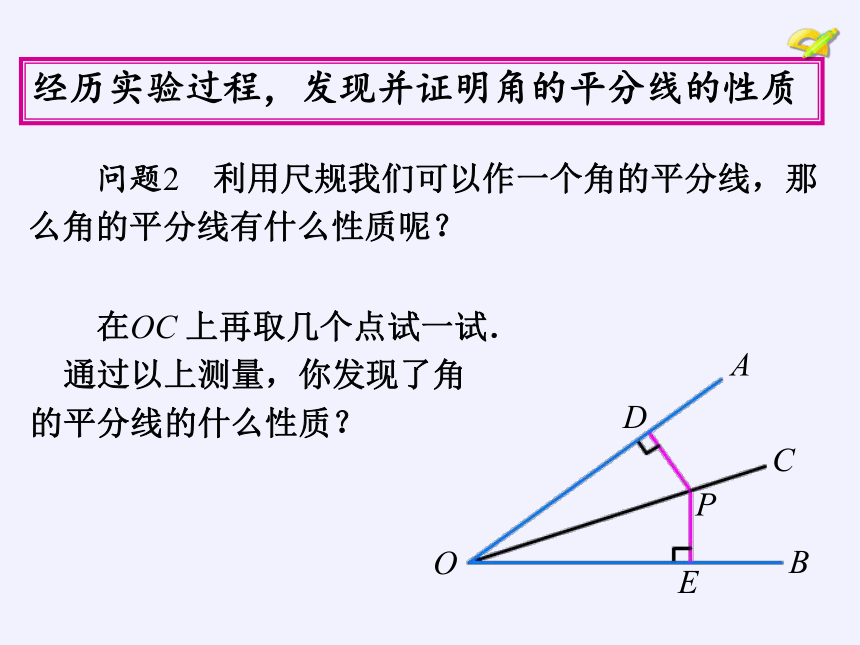
问题2 利用尺规我们可以作一个角的平分线,那
么角的平分线有什么性质呢?
A
B
O
P
C
D
E
经历实验过程,发现并证明角的平分线的性质
问题2 利用尺规我们可以作一个角的平分线,那
么角的平分线有什么性质呢?
在OC 上再取几个点试一试.
通过以上测量,你发现了角
的平分线的什么性质?
A
B
O
P
C
D
E
经历实验过程,发现并证明角的平分线的性质
追问1 通过动手实验、观察比较,我们猜想角平分线有以下性质:
角的平分线上的点到角的两边的距离相等
性质:角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
探究体验
用几何语言表述
追问2 由角的平分线的性质的证明过程,你能概
括出证明几何命题的一般步骤吗?
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用数学符号表示已知和
求证;
(3)经过分析,找出由已知推出求证的途径,写出证
明过程.
经历实验过程,发现并证明角的平分线的性质
追问3 角的平分线的性质的作用是什么?
经历实验过程,发现并证明角的平分线的性质
主要是用于判断和证明两条线段相等,与以前的方
法相比,运用此性质不需要先证两个三角形全等.
P
O
A
B
C
E
D
P
O
A
B
C
E
D
P
O
A
B
C
E
D
A
B
C
D
B
P
O
A
C
E
D
练习1:
下面四个图中,点P都在∠AOB的平分线上,
则图形_____ 中PD=PE.
(2)下图中,PD⊥OA,PE⊥OB,垂足分别为点D、E,
则图中PD=PE吗?
B
P
O
A
C
E
D
解决简单问题,巩固角的平分线的性质
(3)如图,OC 平分∠AOB,点P 在OC 上,PD⊥OA,
垂足为D.若PD =3,则点P 到OB 的距离为3.
解决简单问题,巩固角的平分线的性质
A
B
O
P
C
D
运用本节课所学的知识回答课前引例中的问题:
问题:引例中两条管道的长度有什么关系?理由是什么?
.
P
暖气
天然气
合作交流
M
N
练习2 如图,△ABC中,∠B =∠C,AD 是∠BAC
的平分线, DE⊥AB,DF⊥AC,垂足分别为E,F.求
证:EB =FC.
解决简单问题,巩固角的平分线的性质
A
B
C
D
E
F
[教学内容9]例题讲解
例2 已知:如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA
的距离相等
D
E
F
A
B
C
P
M
N
合作交流
(1)本节课学习了哪些主要内容?
(2)本节课是通过什么方式探究角的平分线的性质的?
(3)角的平分线的性质为我们提供了证明什么的方法?
在应用这一性质时要注意哪些问题?
课堂小结
教科书习题12.3第4、5题.
布置作业
谢 谢
[教学内容1]
生活中有很多数学问题:
小明家居住在通州区一栋居民楼的一楼,刚好位于一条暖气和天然气管道所成角的平分线上的P点,要从P点建两条管道,分别与暖气管道和天然气管道相连.
问题1:怎样修建管道最短?
问题2:新修的两条管道长度有什么关系?.
.
P
暖气
天然气
创设情境
问题1 给你一个角,怎样得到这个角的
平分线?
追问1 你能评价这些方法吗?在生产生活中,这
些方法是否可行呢?
感悟实践经验,用尺规作角的平分线
用量角器度量,也可用折纸的方法.
感悟实践经验,用尺规作角的平分线
追问2 下图是一个平分角的仪器,其中AB =AD,
BC =DC,将点A 放在角的顶点,AB 和AD 沿着角的两
边放下,沿AC 画一条射线AE,AE 就是∠DAB 的平分
线.你能说明它的道理吗?
A
B
D
C
E
A
B
D
C
感悟实践经验,用尺规作角的平分线
追问3 从利用平分角的仪器画角的平分线中,你
受到哪些启发?如何利用直尺和圆规作一个角的平分线?
感悟实践经验,用尺规作角的平分线
利用尺规作角的平分线的具体方法:
A
B
O
M
N
C
(2)分别以M,N为圆心.大于MN一半的长为半径作弧.两弧在∠AOB的内部交于C.
(3)作射线OC 。
则射线OC即为所求。
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
感悟实践经验,用尺规作角的平分线
追问4 你能说明为什么射线OC 是∠AOB 的平分线吗?
A
B
O
M
N
C
经历实验过程,发现并证明角的平分线的性质
如图,任意作一个角∠AOB,作出∠AOB的平分线
OC,在OC 上任取一点P,过点
P 画出OA,OB 的垂线,分别记
垂足为D,E,测量 PD,PE 并
作比较,你得到什么结论?
问题2 利用尺规我们可以作一个角的平分线,那
么角的平分线有什么性质呢?
A
B
O
P
C
D
E
经历实验过程,发现并证明角的平分线的性质
问题2 利用尺规我们可以作一个角的平分线,那
么角的平分线有什么性质呢?
在OC 上再取几个点试一试.
通过以上测量,你发现了角
的平分线的什么性质?
A
B
O
P
C
D
E
经历实验过程,发现并证明角的平分线的性质
追问1 通过动手实验、观察比较,我们猜想角平分线有以下性质:
角的平分线上的点到角的两边的距离相等
性质:角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
探究体验
用几何语言表述
追问2 由角的平分线的性质的证明过程,你能概
括出证明几何命题的一般步骤吗?
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用数学符号表示已知和
求证;
(3)经过分析,找出由已知推出求证的途径,写出证
明过程.
经历实验过程,发现并证明角的平分线的性质
追问3 角的平分线的性质的作用是什么?
经历实验过程,发现并证明角的平分线的性质
主要是用于判断和证明两条线段相等,与以前的方
法相比,运用此性质不需要先证两个三角形全等.
P
O
A
B
C
E
D
P
O
A
B
C
E
D
P
O
A
B
C
E
D
A
B
C
D
B
P
O
A
C
E
D
练习1:
下面四个图中,点P都在∠AOB的平分线上,
则图形_____ 中PD=PE.
(2)下图中,PD⊥OA,PE⊥OB,垂足分别为点D、E,
则图中PD=PE吗?
B
P
O
A
C
E
D
解决简单问题,巩固角的平分线的性质
(3)如图,OC 平分∠AOB,点P 在OC 上,PD⊥OA,
垂足为D.若PD =3,则点P 到OB 的距离为3.
解决简单问题,巩固角的平分线的性质
A
B
O
P
C
D
运用本节课所学的知识回答课前引例中的问题:
问题:引例中两条管道的长度有什么关系?理由是什么?
.
P
暖气
天然气
合作交流
M
N
练习2 如图,△ABC中,∠B =∠C,AD 是∠BAC
的平分线, DE⊥AB,DF⊥AC,垂足分别为E,F.求
证:EB =FC.
解决简单问题,巩固角的平分线的性质
A
B
C
D
E
F
[教学内容9]例题讲解
例2 已知:如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA
的距离相等
D
E
F
A
B
C
P
M
N
合作交流
(1)本节课学习了哪些主要内容?
(2)本节课是通过什么方式探究角的平分线的性质的?
(3)角的平分线的性质为我们提供了证明什么的方法?
在应用这一性质时要注意哪些问题?
课堂小结
教科书习题12.3第4、5题.
布置作业
谢 谢
