人教版八年级上册数学教案:第十二章全等三角形练习课(表格式)
文档属性
| 名称 | 人教版八年级上册数学教案:第十二章全等三角形练习课(表格式) |  | |
| 格式 | zip | ||
| 文件大小 | 38.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 10:39:32 | ||
图片预览

文档简介
课题
全等三角形练习
课型
习题课
总课时
教学目标
1.进一步理解全等三角形的概念。
2.全等三角形的性质和判定的应用。
教学过程
先行独立学习
1、本章知识结构梳理
和学生一起回忆全等三角形的相关知识,然后让个别同学回答,最后全班同学再一起回答,加深记忆,然后老师在课件逐渐的把知识点展现出来,并用红色字体标出答案。
2、方法指引
证明两个三角形全等的基本思路:
(1)已知两边
(2)已知一边一角
(3)已知两角
3.角平分线
1).角平分线性质定理:角平分线上的点到这个角两边的距离相等。
逆定理:
到一个叫两边的距离相等的点在这个角的平分线上
三角形全等是证明线段相等、角相等最基本、最常用的方法。
迁移导入
1、精讲
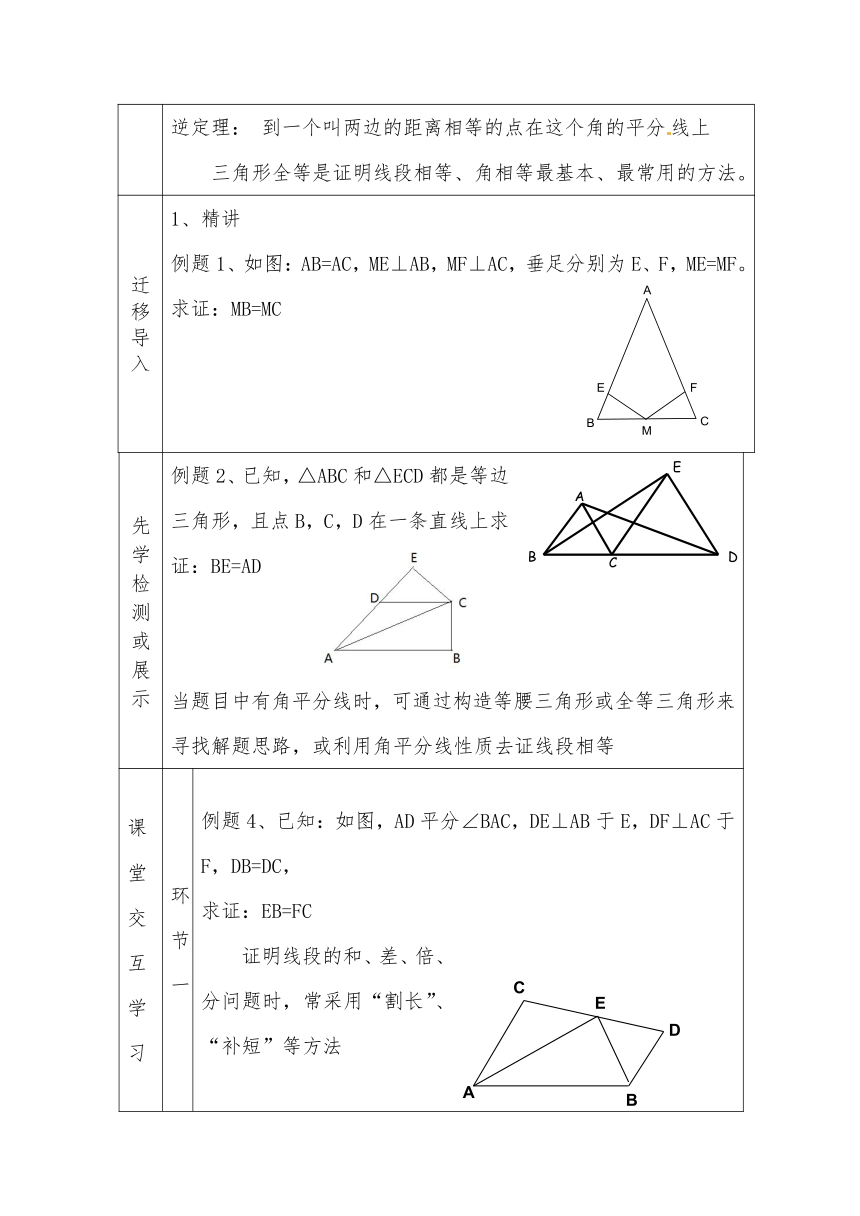
例题1、如图:AB=AC,ME⊥AB,MF⊥AC,垂足分别为E、F,ME=MF。
求证:MB=MC
先学检测或展示
(
E
D
C
A
B
)例题2、已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
当题目中有角平分线时,可通过构造等腰三角形或全等三角形来寻找解题思路,或利用角平分线性质去证线段相等
课堂交互学习
环节一
?
例题4、已知:如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,DB=DC,
求证:EB=FC
(
A
C
E
B
D
)
证明线段的和、差、倍、分问题时,常采用“割长”、“补短”等方法
环节二
?例题5、如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证AB=AC+BD
提示:要证明两条线段的和与一条线段相等时常用的两种方法:(1)、可在长线段上截取与两条线段中一条相等的一段,然后证明剩余的线段与另一条线段相等。(割)
(2)、把一个三角形移到另一位置,使两线段补成一条线段,再证明它与长线段相等。(补))
整体达标检测
(
G
F
E
D
C
B
A
)3、如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。(只写出一种情况)①AB=AC
②DE=DF
③BE=CF
已知:EG∥AF,________,__________
求证:_________
拓展巩固练习
4、如图,在R△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E,求证:BC垂直且平分DE
教学反思
全等三角形练习
课型
习题课
总课时
教学目标
1.进一步理解全等三角形的概念。
2.全等三角形的性质和判定的应用。
教学过程
先行独立学习
1、本章知识结构梳理
和学生一起回忆全等三角形的相关知识,然后让个别同学回答,最后全班同学再一起回答,加深记忆,然后老师在课件逐渐的把知识点展现出来,并用红色字体标出答案。
2、方法指引
证明两个三角形全等的基本思路:
(1)已知两边
(2)已知一边一角
(3)已知两角
3.角平分线
1).角平分线性质定理:角平分线上的点到这个角两边的距离相等。
逆定理:
到一个叫两边的距离相等的点在这个角的平分线上
三角形全等是证明线段相等、角相等最基本、最常用的方法。
迁移导入
1、精讲
例题1、如图:AB=AC,ME⊥AB,MF⊥AC,垂足分别为E、F,ME=MF。
求证:MB=MC
先学检测或展示
(
E
D
C
A
B
)例题2、已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
当题目中有角平分线时,可通过构造等腰三角形或全等三角形来寻找解题思路,或利用角平分线性质去证线段相等
课堂交互学习
环节一
?
例题4、已知:如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,DB=DC,
求证:EB=FC
(
A
C
E
B
D
)
证明线段的和、差、倍、分问题时,常采用“割长”、“补短”等方法
环节二
?例题5、如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证AB=AC+BD
提示:要证明两条线段的和与一条线段相等时常用的两种方法:(1)、可在长线段上截取与两条线段中一条相等的一段,然后证明剩余的线段与另一条线段相等。(割)
(2)、把一个三角形移到另一位置,使两线段补成一条线段,再证明它与长线段相等。(补))
整体达标检测
(
G
F
E
D
C
B
A
)3、如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。(只写出一种情况)①AB=AC
②DE=DF
③BE=CF
已知:EG∥AF,________,__________
求证:_________
拓展巩固练习
4、如图,在R△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E,求证:BC垂直且平分DE
教学反思
