人教版八年级数学上册 13.1.1轴对称 能力提升卷(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 13.1.1轴对称 能力提升卷(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 419.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 00:00:00 | ||
图片预览


文档简介
人教版八年级数学上册
13.1.1轴对称
能力提升卷
一、选择题(共10小题,3
10=30)
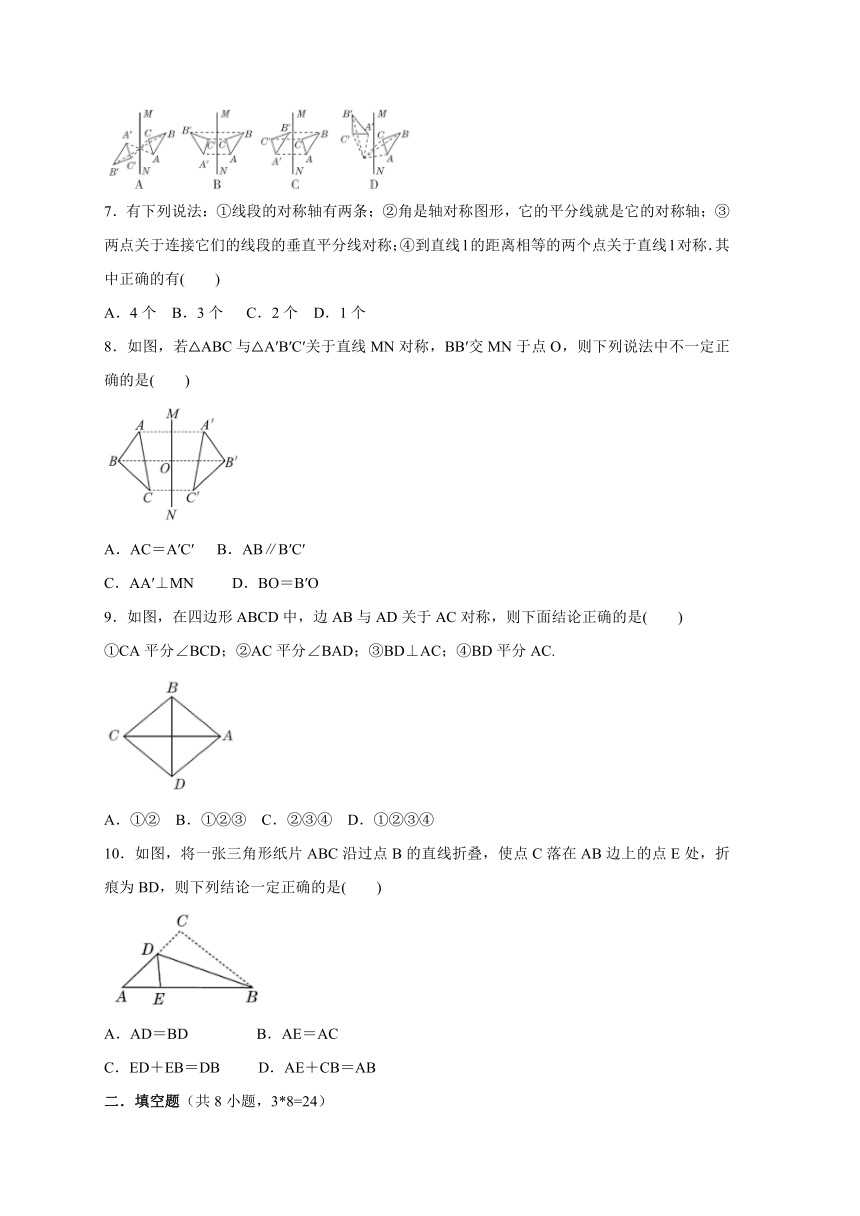
1.在一些汉字的美术字中,有的是轴对称图形,下面四个美术字中可以看作轴对称图形的是( )
2.甲骨文是我国的一种古代文字,下面是“北”“比”“鼎”“射”四个字的甲骨文,其中不是轴对称图形的是( )
3.下列图形:
其中,是轴对称图形且只有两条对称轴的是( )
A.①②
B.②③
C.②④
D.③④
4.如图的五角星是轴对称图形,它的对称轴共有( )
A.1条
B.3条
C.5条
D.无数条
5.如图所示的4组图形中,成轴对称的有( ).
A.4组
B.3组
C.2组
D.1组
6.
下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
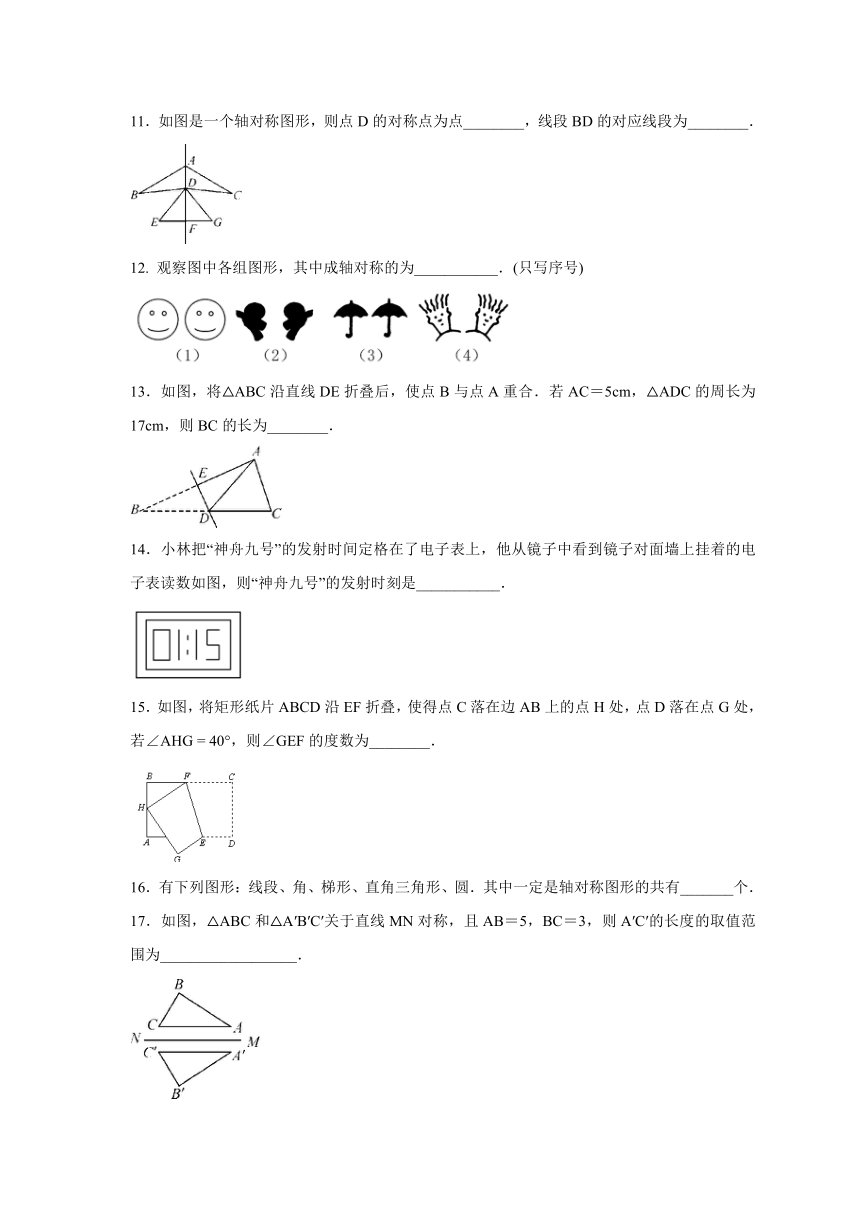
7.有下列说法:①线段的对称轴有两条;②角是轴对称图形,它的平分线就是它的对称轴;③两点关于连接它们的线段的垂直平分线对称;④到直线l的距离相等的两个点关于直线l对称.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
8.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是( )
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
9.如图,在四边形ABCD中,边AB与AD关于AC对称,则下面结论正确的是( )
①CA平分∠BCD;②AC平分∠BAD;③BD⊥AC;④BD平分AC.
A.①② B.①②③ C.②③④ D.①②③④
10.如图,将一张三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD
B.AE=AC
C.ED+EB=DB
D.AE+CB=AB
二.填空题(共8小题,3
8=24)
11.如图是一个轴对称图形,则点D的对称点为点________,线段BD的对应线段为________.
12.
观察图中各组图形,其中成轴对称的为___________.(只写序号)
13.如图,将△ABC沿直线DE折叠后,使点B与点A重合.若AC=5cm,△ADC的周长为17cm,则BC的长为________.
14.小林把“神舟九号”的发射时间定格在了电子表上,他从镜子中看到镜子对面墙上挂着的电子表读数如图,则“神舟九号”的发射时刻是___________.
15.如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG
=
40°,则∠GEF的度数为________.
16.有下列图形:线段、角、梯形、直角三角形、圆.其中一定是轴对称图形的共有_______个.
17.如图,△ABC和△A′B′C′关于直线MN对称,且AB=5,BC=3,则A′C′的长度的取值范围为__________________.
18.如图,在△ABC中,AC=BC,∠ACB=90°,点D,E在AB上,将△ACD,△BCE分别沿CD,CE翻折,点A,B分别落在点A',B'的位置,再将△A'CD,△B'CE分别沿A'C,B'C翻折,点D与点E恰好重合于点O,则∠A'CB'的度数是________.
三.解答题(共7小题,
46分)
19.(6分)
如图,找出图中的轴对称图形,并说出它们各有几条对称轴?
20.(6分)
如图,AD为△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则E、F一定关于AD对称,为什么?
21.(6分)
如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,求∠E的度数。
22.(6分)
如图所示,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F.
若MN=20
cm,求△PEF的周长;
23.(6分)
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处.
(1)求证:△FGC≌△EBC.
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
24.(8分)
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,求∠AMN+∠ANM的度数.
25.(8分)
如图,O为△ABC内部一点,OB=3,P、R为O分别以直线AB、直线BC为对称轴的对称点.
(1)请指出当∠ABC为多少度时,会使得PR的长度等于6,并说明理由;
(2)结合(1),请判断当∠ABC不是你指出的角度时,PR的长度是小于6还是大于6,并说明理由.
参考答案
1-5
DBACD
6-10DCBBD
11.
D,CD
12.
(1)(2)(4)
13.
12cm
14.
21:10
15.
110°
16.
3
17.
2<A′C′<8
18.
30°
19.
解:⑴是轴对称图形,有3条对称轴;
⑵是轴对称图形,有5条对称轴;
⑶是轴对称图形,有4条对称轴;
⑷是轴对称图形,有1条对称轴;
⑸是轴对称图形,有2条对称轴;
⑹不是轴对称图形.
20.
证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∴点D在EF的垂直平分线上.
在Rt△AED和Rt△AFD中,DE=DF,AD=AD,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∴点A在EF的垂直平分线上.
∴AD垂直平分EF,
∴E、F关于AD对称.
21.
解:∵AD∥BC,∴∠ADB=∠DBC.
由折叠可得∠ADB=∠BDF,∠E=∠A.
∴∠DBC=∠BDF.
∵∠CFD=40°,∴∠DBC=∠BDF=∠ADB=20°.
又∵∠ABD=48°,
∴在△ABD中,∠A=180°-20°-48°=112°.
∴∠E=∠A=112°.
22.
解:如图,设MP与OA相交于点R,PN与OB相交于点T.
∵点M,N分别是点P关于直线OA,OB的对称点,
∴OA垂直平分PM,OB垂直平分PN,
∴MR=PR,∠MRE=∠PRE=90°,
PT=NT,∠PTF=∠NTF=90°.
又∵RE=RE,∴△MRE≌△PRE(SAS),∴ME=PE.
又∵FT=FT,∴△PTF≌△NTF(SAS),
∴NF=PF,
∴PE+EF+PF=ME+EF+NF=MN=20
cm,
即△PEF的周长是20
cm.
23.
(1)证明:由题意知∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.又∵∠G=∠D=∠B=90°,GC=AD=BC,
∴△FGC≌△EBC(ASA).
(2)解:∵△FGC≌△EBC,∴GF=BE.
又∵DF=GF,∴DF=BE.
∴四边形ECGF的面积=四边形AEFD的面积=====16.
24.
解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠EAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM
=∠MA′A+∠MAA′+∠NAD+∠A″
=2(∠AA′M+∠A″)
=2×60°
=120°,
25.
解:(1)当∠ABC=90°时,PR=6.
证明:如图,连接PB、RB,
∵P、R为O分别以直线AB、直线BC为对称轴的对称点,∴PB=OB=3,RB=OB=3,∵∠ABC=90°,
∴∠ABP+∠CBR=∠ABO+∠CBO=∠ABC=90°,
∴P、B、R三点共线,∴PR=2×3=6.
(2)PR的长度小于6.
理由:当∠ABC≠90°时,P、B、R三点不在同一直线上,
∴PB+BR>PR,∵PB+BR=2OB=2×3=6,∴PR<6.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
13.1.1轴对称
能力提升卷
一、选择题(共10小题,3
10=30)
1.在一些汉字的美术字中,有的是轴对称图形,下面四个美术字中可以看作轴对称图形的是( )
2.甲骨文是我国的一种古代文字,下面是“北”“比”“鼎”“射”四个字的甲骨文,其中不是轴对称图形的是( )
3.下列图形:
其中,是轴对称图形且只有两条对称轴的是( )
A.①②
B.②③
C.②④
D.③④
4.如图的五角星是轴对称图形,它的对称轴共有( )
A.1条
B.3条
C.5条
D.无数条
5.如图所示的4组图形中,成轴对称的有( ).
A.4组
B.3组
C.2组
D.1组
6.
下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
7.有下列说法:①线段的对称轴有两条;②角是轴对称图形,它的平分线就是它的对称轴;③两点关于连接它们的线段的垂直平分线对称;④到直线l的距离相等的两个点关于直线l对称.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
8.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是( )
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
9.如图,在四边形ABCD中,边AB与AD关于AC对称,则下面结论正确的是( )
①CA平分∠BCD;②AC平分∠BAD;③BD⊥AC;④BD平分AC.
A.①② B.①②③ C.②③④ D.①②③④
10.如图,将一张三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD
B.AE=AC
C.ED+EB=DB
D.AE+CB=AB
二.填空题(共8小题,3
8=24)
11.如图是一个轴对称图形,则点D的对称点为点________,线段BD的对应线段为________.
12.
观察图中各组图形,其中成轴对称的为___________.(只写序号)
13.如图,将△ABC沿直线DE折叠后,使点B与点A重合.若AC=5cm,△ADC的周长为17cm,则BC的长为________.
14.小林把“神舟九号”的发射时间定格在了电子表上,他从镜子中看到镜子对面墙上挂着的电子表读数如图,则“神舟九号”的发射时刻是___________.
15.如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG
=
40°,则∠GEF的度数为________.
16.有下列图形:线段、角、梯形、直角三角形、圆.其中一定是轴对称图形的共有_______个.
17.如图,△ABC和△A′B′C′关于直线MN对称,且AB=5,BC=3,则A′C′的长度的取值范围为__________________.
18.如图,在△ABC中,AC=BC,∠ACB=90°,点D,E在AB上,将△ACD,△BCE分别沿CD,CE翻折,点A,B分别落在点A',B'的位置,再将△A'CD,△B'CE分别沿A'C,B'C翻折,点D与点E恰好重合于点O,则∠A'CB'的度数是________.
三.解答题(共7小题,
46分)
19.(6分)
如图,找出图中的轴对称图形,并说出它们各有几条对称轴?
20.(6分)
如图,AD为△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则E、F一定关于AD对称,为什么?
21.(6分)
如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,求∠E的度数。
22.(6分)
如图所示,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F.
若MN=20
cm,求△PEF的周长;
23.(6分)
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处.
(1)求证:△FGC≌△EBC.
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
24.(8分)
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,求∠AMN+∠ANM的度数.
25.(8分)
如图,O为△ABC内部一点,OB=3,P、R为O分别以直线AB、直线BC为对称轴的对称点.
(1)请指出当∠ABC为多少度时,会使得PR的长度等于6,并说明理由;
(2)结合(1),请判断当∠ABC不是你指出的角度时,PR的长度是小于6还是大于6,并说明理由.
参考答案
1-5
DBACD
6-10DCBBD
11.
D,CD
12.
(1)(2)(4)
13.
12cm
14.
21:10
15.
110°
16.
3
17.
2<A′C′<8
18.
30°
19.
解:⑴是轴对称图形,有3条对称轴;
⑵是轴对称图形,有5条对称轴;
⑶是轴对称图形,有4条对称轴;
⑷是轴对称图形,有1条对称轴;
⑸是轴对称图形,有2条对称轴;
⑹不是轴对称图形.
20.
证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∴点D在EF的垂直平分线上.
在Rt△AED和Rt△AFD中,DE=DF,AD=AD,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∴点A在EF的垂直平分线上.
∴AD垂直平分EF,
∴E、F关于AD对称.
21.
解:∵AD∥BC,∴∠ADB=∠DBC.
由折叠可得∠ADB=∠BDF,∠E=∠A.
∴∠DBC=∠BDF.
∵∠CFD=40°,∴∠DBC=∠BDF=∠ADB=20°.
又∵∠ABD=48°,
∴在△ABD中,∠A=180°-20°-48°=112°.
∴∠E=∠A=112°.
22.
解:如图,设MP与OA相交于点R,PN与OB相交于点T.
∵点M,N分别是点P关于直线OA,OB的对称点,
∴OA垂直平分PM,OB垂直平分PN,
∴MR=PR,∠MRE=∠PRE=90°,
PT=NT,∠PTF=∠NTF=90°.
又∵RE=RE,∴△MRE≌△PRE(SAS),∴ME=PE.
又∵FT=FT,∴△PTF≌△NTF(SAS),
∴NF=PF,
∴PE+EF+PF=ME+EF+NF=MN=20
cm,
即△PEF的周长是20
cm.
23.
(1)证明:由题意知∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.又∵∠G=∠D=∠B=90°,GC=AD=BC,
∴△FGC≌△EBC(ASA).
(2)解:∵△FGC≌△EBC,∴GF=BE.
又∵DF=GF,∴DF=BE.
∴四边形ECGF的面积=四边形AEFD的面积=====16.
24.
解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠EAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM
=∠MA′A+∠MAA′+∠NAD+∠A″
=2(∠AA′M+∠A″)
=2×60°
=120°,
25.
解:(1)当∠ABC=90°时,PR=6.
证明:如图,连接PB、RB,
∵P、R为O分别以直线AB、直线BC为对称轴的对称点,∴PB=OB=3,RB=OB=3,∵∠ABC=90°,
∴∠ABP+∠CBR=∠ABO+∠CBO=∠ABC=90°,
∴P、B、R三点共线,∴PR=2×3=6.
(2)PR的长度小于6.
理由:当∠ABC≠90°时,P、B、R三点不在同一直线上,
∴PB+BR>PR,∵PB+BR=2OB=2×3=6,∴PR<6.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
