人教版九年级上册 数学 24.1.3弧、弦、圆心角课件(共20张PPT)
文档属性
| 名称 | 人教版九年级上册 数学 24.1.3弧、弦、圆心角课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 247.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 17:15:13 | ||
图片预览



文档简介
(共20张PPT)
24.1.3弧、弦、圆心角
O
B
A
C
D
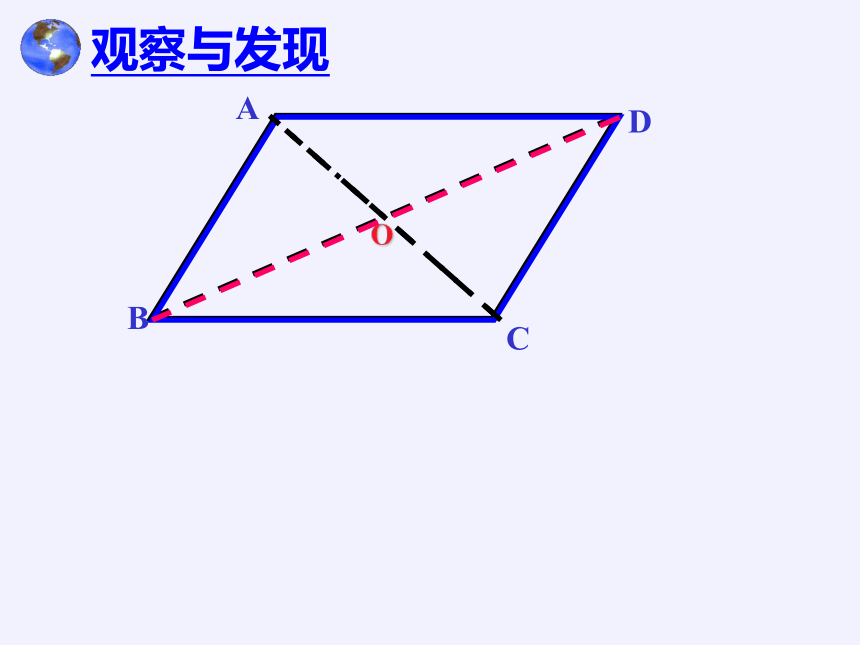
观察与发现
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心.
思考:
·
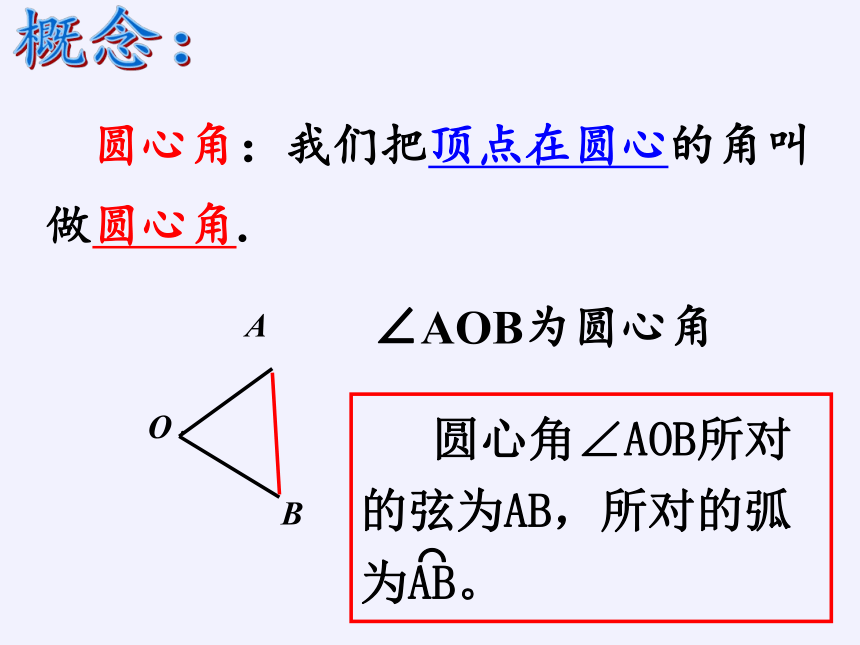
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
概念:
圆心角∠AOB所对的弦为AB,所对的弧为AB。
⌒
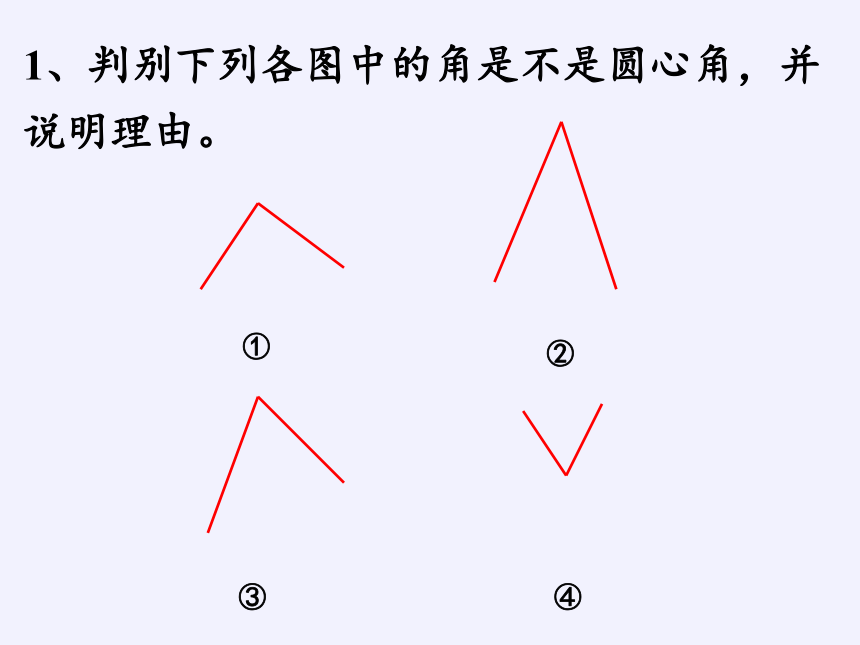
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
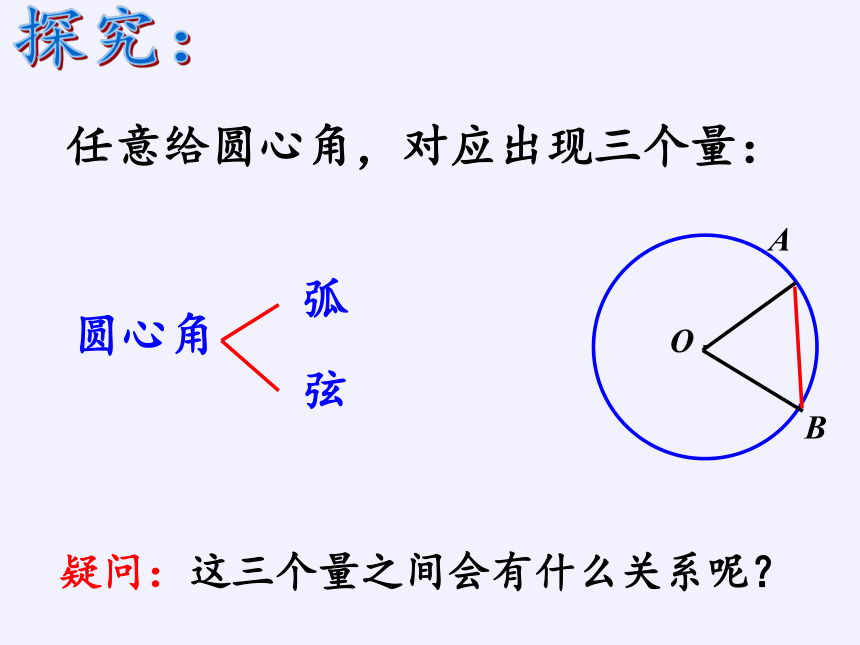
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
探究:
疑问:这三个量之间会有什么关系呢?
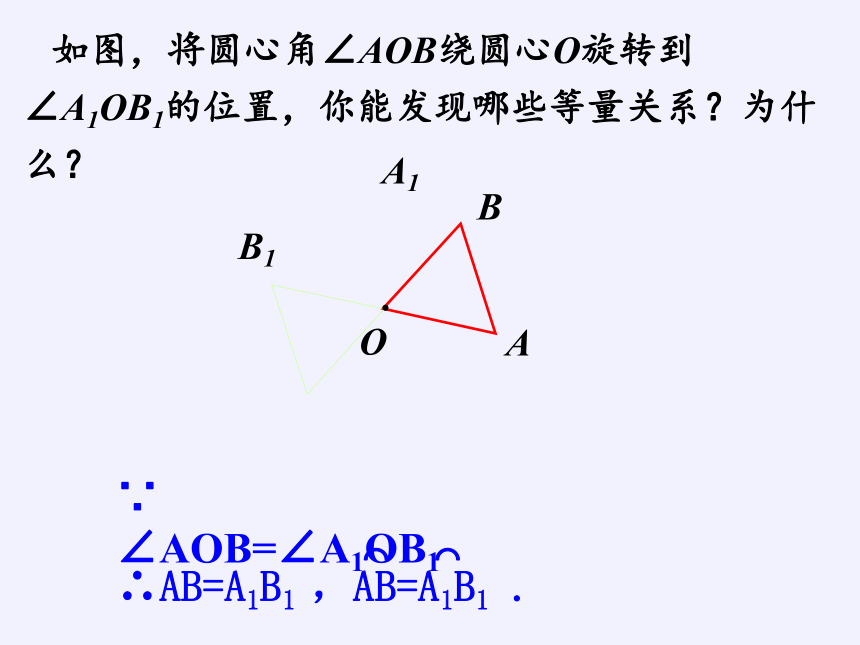
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵
∠AOB=∠A1OB1
∴AB=A1B1
,AB=A1B1
.
⌒
⌒
·
O
A
B
A1
·
O1
B1
·
如图,⊙O与⊙O1是等圆,∠AOB
=∠A1OB1=600,请问上述结论还成立吗?为什么?
∵
∠AOB=∠A1OB1
∴AB=A1B1
,AB=A1B1
.
⌒
⌒
O
α
A
B
A1
B1
α
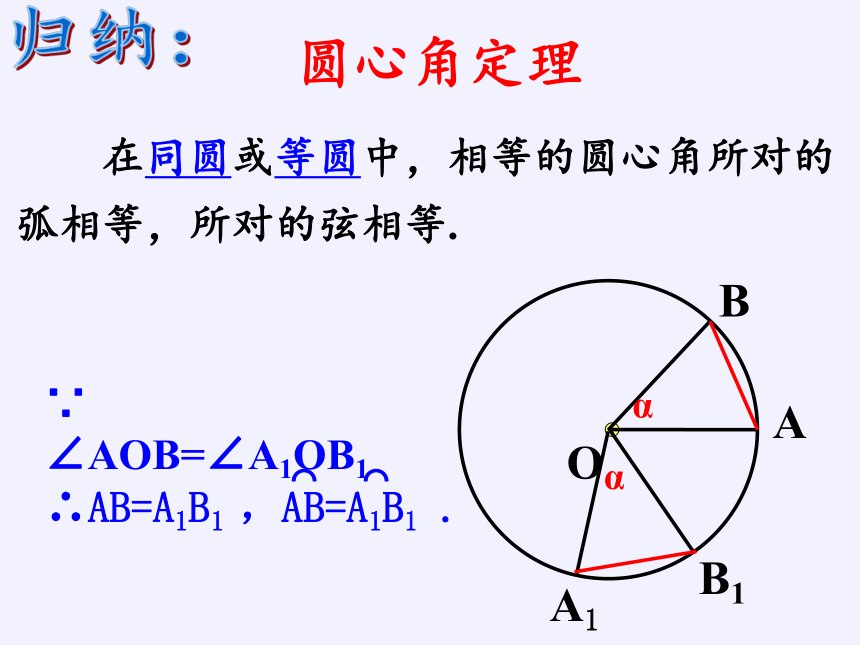
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
归纳:
∵
∠AOB=∠A1OB1
∴AB=A1B1
,AB=A1B1
.
⌒
⌒
圆心角定理
思考:
在同圆或等圆中,如果两条弧相等,你能得什么结论?
在同圆或等圆中,如果两条弦相等呢?
O
α
A
B
A1
B1
α
同圆或等圆中,两个圆心角、两条圆心角所对的弧、两条圆心角所对的弦中如果有一组量相等,它们所对应的其余各组量也相等。
等对等定理
延伸:
(1)
圆心角
(2)
弧
(3)
弦
知一得二
等对等定理整体理解:
O
α
A
B
A1
B1
α
1、如图3,AB、CD是⊙O的两条弦。
(1)如果AB=CD,那么
,
。
(2)如果弧AB=弧CD,那么
,
。
(3)如果∠AOB=∠COD,那么
,
。
(4)如果AB=CD,OE⊥AB于E,
OF⊥CD于F,OE与OF相等吗?
为什么?
巩固:
证明:
∵AB=AC
∴AB=AC,△ABC是等腰三角形
又
∠ACB=60°
∴△ABC是等边三角形,AB=BC=CA
∴∠AOB=∠BOC=∠AOC
例1
如图1,在⊙O中,AB=AC,∠ACB=60°,
求证∠AOB=∠BOC=∠AOC。
例题:
⌒
⌒
⌒
⌒
O
B
C
A
2、如图4,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数。
O
A
B
E
D
C
证明:
∵
BC=CD=DE
∴∠COB=∠COD=∠DOE=35°
∴∠AOE=1800-∠COB-∠COD-∠DOE
=750
⌒
⌒
⌒
⌒
⌒
⌒
3、如图6,AD=BC,那么比较AB与CD的大小.
O
D
C
A
B
⌒
⌒
4、如图7所示,CD为⊙O的弦,在CD上取
CE=DF,连结OE、OF,并延长交⊙O于点A、
B.
(1)试判断△OEF的形状,并说明理由;
(2)求证:AC=BD
⌒
⌒
E
F
O
A
B
C
D
5、如图,等边△ABC的三个顶点A、B、C都在⊙O上,连接OA、OB、OC,延长AO分别交BC于点P,交BC于点D,连接BD、CD.
(1)判断四边形BDCO的形状,并说明理由;
(2)若⊙O的半径为r,求△ABC的边长
⌒
B
C
A
O
P
D
1、三个元素:
圆心角、弦、弧
归纳:
2、三个相等关系:
O
α
A
B
A1
B1
α
(1)
圆心角相等
(2)
弧相等
(3)
弦相等
知一得二
谢
谢
24.1.3弧、弦、圆心角
O
B
A
C
D
观察与发现
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心.
思考:
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
概念:
圆心角∠AOB所对的弦为AB,所对的弧为AB。
⌒
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
探究:
疑问:这三个量之间会有什么关系呢?
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵
∠AOB=∠A1OB1
∴AB=A1B1
,AB=A1B1
.
⌒
⌒
·
O
A
B
A1
·
O1
B1
·
如图,⊙O与⊙O1是等圆,∠AOB
=∠A1OB1=600,请问上述结论还成立吗?为什么?
∵
∠AOB=∠A1OB1
∴AB=A1B1
,AB=A1B1
.
⌒
⌒
O
α
A
B
A1
B1
α
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
归纳:
∵
∠AOB=∠A1OB1
∴AB=A1B1
,AB=A1B1
.
⌒
⌒
圆心角定理
思考:
在同圆或等圆中,如果两条弧相等,你能得什么结论?
在同圆或等圆中,如果两条弦相等呢?
O
α
A
B
A1
B1
α
同圆或等圆中,两个圆心角、两条圆心角所对的弧、两条圆心角所对的弦中如果有一组量相等,它们所对应的其余各组量也相等。
等对等定理
延伸:
(1)
圆心角
(2)
弧
(3)
弦
知一得二
等对等定理整体理解:
O
α
A
B
A1
B1
α
1、如图3,AB、CD是⊙O的两条弦。
(1)如果AB=CD,那么
,
。
(2)如果弧AB=弧CD,那么
,
。
(3)如果∠AOB=∠COD,那么
,
。
(4)如果AB=CD,OE⊥AB于E,
OF⊥CD于F,OE与OF相等吗?
为什么?
巩固:
证明:
∵AB=AC
∴AB=AC,△ABC是等腰三角形
又
∠ACB=60°
∴△ABC是等边三角形,AB=BC=CA
∴∠AOB=∠BOC=∠AOC
例1
如图1,在⊙O中,AB=AC,∠ACB=60°,
求证∠AOB=∠BOC=∠AOC。
例题:
⌒
⌒
⌒
⌒
O
B
C
A
2、如图4,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数。
O
A
B
E
D
C
证明:
∵
BC=CD=DE
∴∠COB=∠COD=∠DOE=35°
∴∠AOE=1800-∠COB-∠COD-∠DOE
=750
⌒
⌒
⌒
⌒
⌒
⌒
3、如图6,AD=BC,那么比较AB与CD的大小.
O
D
C
A
B
⌒
⌒
4、如图7所示,CD为⊙O的弦,在CD上取
CE=DF,连结OE、OF,并延长交⊙O于点A、
B.
(1)试判断△OEF的形状,并说明理由;
(2)求证:AC=BD
⌒
⌒
E
F
O
A
B
C
D
5、如图,等边△ABC的三个顶点A、B、C都在⊙O上,连接OA、OB、OC,延长AO分别交BC于点P,交BC于点D,连接BD、CD.
(1)判断四边形BDCO的形状,并说明理由;
(2)若⊙O的半径为r,求△ABC的边长
⌒
B
C
A
O
P
D
1、三个元素:
圆心角、弦、弧
归纳:
2、三个相等关系:
O
α
A
B
A1
B1
α
(1)
圆心角相等
(2)
弧相等
(3)
弦相等
知一得二
谢
谢
同课章节目录
