人教版九年级数学上册课件: 24.2.1:点和圆的位置关系(共44张PPT)
文档属性
| 名称 | 人教版九年级数学上册课件: 24.2.1:点和圆的位置关系(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 706.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 17:13:58 | ||
图片预览









文档简介
(共44张PPT)
点和圆的位置关系
我国射击运动员在奥运会上获金牌,为我国赢得荣誉,图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的.
你知道击中靶上不同位置的成绩是如何计算的吗?
解决这个问题就要研究点和圆的位置关系.
探究
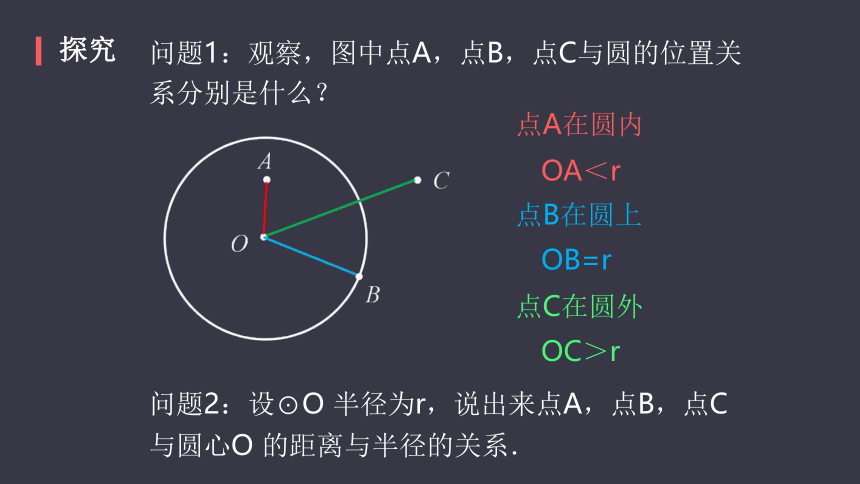
问题1:观察,图中点A,点B,点C与圆的位置关系分别是什么?
问题2:设⊙O
半径为r,说出来点A,点B,点C
与圆心O
的距离与半径的关系.
点A在圆内
OA<r
点B在圆上
OB=r
点C在圆外
OC>r
探究
问题3:反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
OA<r
点A在圆内
OB=r
点B在圆上
OC>r
点C在圆外
归纳
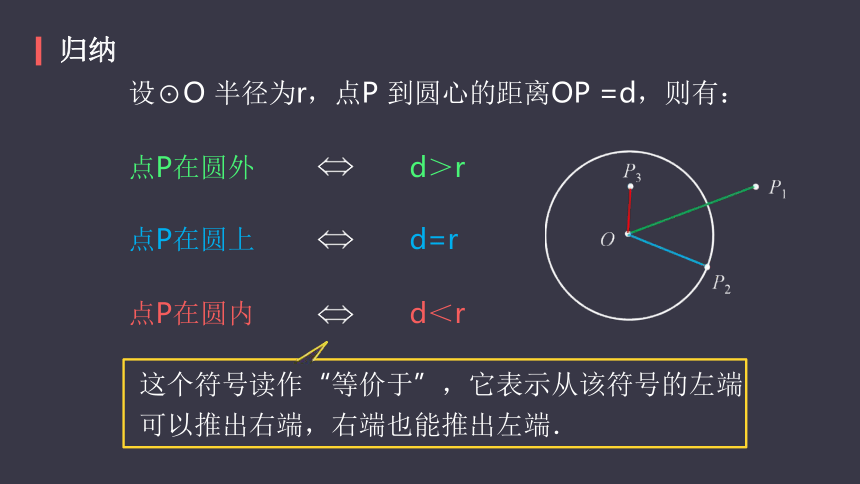
设⊙O
半径为r,点P
到圆心的距离OP
=d,则有:
点P在圆外
d>r
点P在圆上
d=r
点P在圆内
d<r
这个符号读作“等价于”,它表示从该符号的左端可以推出右端,右端也能推出左端.
你知道击中靶上不同位置的成绩是如何计算的吗
?
射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域.
这些区域用由高到底的环数来表示,射击成绩
用弹着点位置对应的环数来表示.
弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.
例题
已知⊙O
的半径为10cm,A,B,C
三点到圆心O
的距离分别为8cm,10cm,12cm,则点A,B,C
与⊙O
的位置关系是:
点A在_________.
点B在_________.
点C在_________.
圆内
圆上
圆外
例题
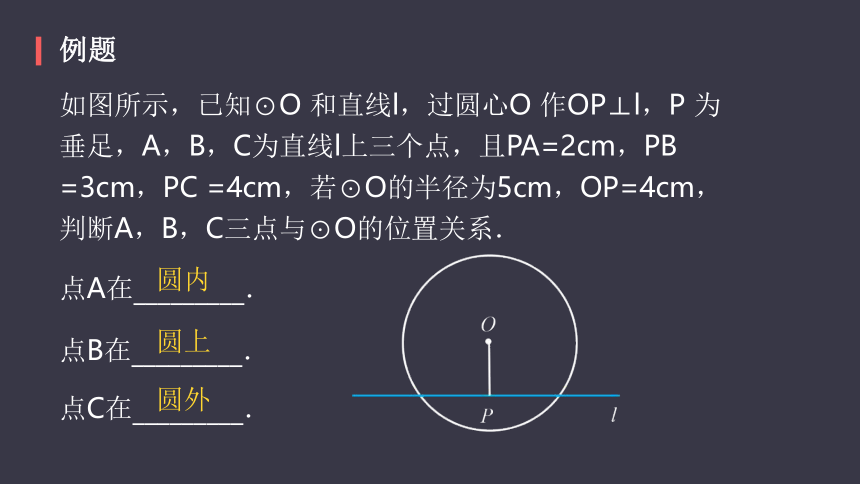
如图所示,已知⊙O
和直线l,过圆心O
作OP⊥l,P
为垂足,A,B,C为直线l上三个点,且PA=2cm,PB
=3cm,PC
=4cm,若⊙O的半径为5cm,OP=4cm,判断A,B,C三点与⊙O的位置关系.
点A在_________.
点B在_________.
点C在_________.
圆内
圆上
圆外
例题
已知⊙O
的半径为
5,圆心
O
的坐标为(0,0),若点
P
的坐标为(4,2),点
P
与⊙O
的位置关系是____________________.
由勾股定理可知,
所以
点P在⊙O内
练习
已知⊙O
的半径为4,OP=3.4,则P
在⊙O
的________.
内部
练习
已知
点P
在
⊙O
的外部,OP=5,那么⊙O
的半径r满足_____________.
0<r<5
练习
已知⊙O
的半径为5,M
为ON的中点,当OM=3时,N点与⊙O
的位置关系是N
在⊙O
的_____________.
外部
练习
⊙O
直径为d,点A到圆心的距离为m,若点
A不在圆
外,则d与m的关系是_____________.
练习
有一张矩形纸片,AB
=3cm,AD
=4cm,若以A为圆心作圆,并且要使点D
在⊙A内,而点C
在⊙A外,
⊙A的半径
r
的取值范围是__________________.
补充题
⊙O
的半径为
5
cm,O
到直线l的距离OP=3cm,Q
为l上一点且PQ
=4.2cm,点Q
在⊙O
_________.
外
补充题
如图,
数轴上半径为1的⊙O
从原点O
开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P
以每秒2个单位的速度向左运动,经过_________秒后,点P在⊙O
上.
2或
我们知道,已知______和_______,可以确定一个圆.
问题1:经过一个已知点A能不能作圆,能作多少个圆?
能作无数个圆
A
圆心
半径
过一个点作圆
.
我们知道,已知______和_______,可以确定一个圆.
问题2:经过两个已知点A,B,能不能作圆?
圆心有什么特点?
由于圆心到A,B
的距离相等,
所以圆心在线段AB
的垂直平分线上.
圆心
半径
A
B
过两个点作圆
探究
总结:过已知点作圆,关键就是确定______.
问题3:经过不在同一直线上的三个点A,B,C
能不能作圆?如果能,怎么确定圆心?
圆心
圆心O到A,B,C
的距离都相等
所以O
既在线段AB
的垂直平分线上
又在线段BC
的垂直平分线上
垂直平分线的交点就是圆心O
以O为圆心,OA(
或OB,OC
)为半径作圆即为所求.
B
C
A
O
问题4:经过不在同一直线上的三个点A,B,C
能作几个圆?
由于圆心O是唯一确定的,
所以圆也是唯一确定的.
?
?不在同一条直线上
的三个点确定一个圆.
过三个点作圆
因为
?不在同一条直线上
的三个点确定一个圆.
所以
经过三角形的三个顶点一定可以作一个圆.
这个圆叫做三角形的外接圆.
外接圆的圆心是三角形三条边的_______________的交点,
叫做三角形的外心.
垂直平分线
三角形的外接圆
例题
一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
答案:关键就是确定圆心.
圆弧边缘任取三个点,
然后连接其中任意两组点,作它们的垂直平分线,
所得交点就是圆心,
进而可以画出整个圆.
练习
直角三角形的外心是______的中点,
锐角三角形的外心在三角形______,
钝角三角形的外心在三角形_______.
斜边
内部
外部
练习
三角形的外心具有的性质是
(?
?
?
?)
A.到三个顶点的距离相等
B.到三边的距离相等
C.是三角形三条角平分线的交点
D.是三角形三条中线的交点
A
练习
下列命题中不正确的是
(?
?
?
?)
A.圆有且只有一个内接三角形
B.三角形只有一个外接圆
C.三角形的外心是这个三角形任意两边的垂直平分线的交点
D.等边三角形的外心也是三角形的三条中线、高、角平分线的交点
A
练习
判断:
1.经过三点一定可以作圆.(?
?
?
)
2.三角形的外心就是这个三角形两边垂直平分线
的交点.(?
?
?)
3.三角形的外心到三边的距离相等.(?
?
?
)
练习
如图,黑猫警长发现一只老鼠溜进了一个内部连通的鼠洞,鼠洞只有三个出口A,B,C.要想同时顾及这三个出口以防老鼠出洞,黑猫警长最好蹲守在(?
?
?)
A.△ABC
的三边高线的交点P处
B.
△ABC
的三角平分线的交点P处
C.
△ABC
的三边中线的交点P处
D.
△ABC
的三边中垂线的交点P处
D
补充题
若
A、B、C
为平面上的三点,
AB
=2,BC
=3,AC
=5,
则(?
?
?)
D
A.可以画一个圆,使A,B,C
都在圆周上
B
.可以画一个圆,使A,B
在圆周上,C
在圆内
C
.可以画一个圆,使A,C
在圆周上,B
在圆外
D
.可以画一个圆,使A,C
在圆周上,B
在圆内
思考
经过同一条直线上的三个点能作出一个圆吗?
如图,假设过同一条直线l上三点A、B、C
可以做一个圆,设这个圆的圆心为P,
那么点P既在线段AB
的垂直平分线l?
上,
又在线段BC
的垂直平分线l?
上,
即点P
为l?
与l?
的交点.
讨论一下:你们能发现什么不对劲的地方吗?
P
思考
经过同一条直线上的三个点能作出一个圆吗?
如图,假设过同一条直线l上三点A、B、C
可以做一个圆,设这个圆的圆心为P,
l?
⊥l,l?
⊥l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直相矛盾,
假设不成立,所以过同一条直线上的三点不能做圆.
反证法
上面的证明“过同一条直线上的三点不能做圆”的方法与我们以前学过的证明不同,
它不是直接从命题的已知得结论,?
?
?
?
?而是假设命题的结论不成立
由此经过推理的出矛盾,由矛盾判定假设不正确,
从而得到原命题成立,
这种方法叫做反证法.
用反证法证明平行线的性质“两直线平行,同位角相等”.
已知AB∥CD,求证:∠1=∠2.
假设∠1≠∠2,过点O
作A’B’,
使∠EOB’=∠2.
根据“同位角相等,两直线平行”,
可得A’B’∥CD.
由此可知,过点O
的直线AB和直线A’B’都与直线CD平行.
讨论一下,你们能发现矛盾之处吗?
平行线性质定理的证明
用反证法证明平行线的性质“两直线平行,同位角相等”.
已知AB∥CD,求证:∠1=∠2.
由此可知,过点O
的直线AB
和直线A’B’都与直线CD
平行.
这与平行公理“过直线外一点有且只有一条直线与已知直线平行”矛盾.
这说明假设∠1≠∠2不正确,
从而∠1=∠2.
平行线性质定理的证明
练习
画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
练习
体育课上,小明和小雨的铅球成绩分别是6.4m和5.1m,他们投出的铅球分别落在图中哪个区域内.
练习
如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.
在⊙O
中,点M
到⊙O的最小距离为3,最大距离是19,那么⊙O
的半径为__________.
11或8
点到圆的距离最值
点到圆的距离最值
一个点与定圆上最近点的距离为
4
cm,最远点的距离为
9
cm,则此圆的半径为________________.
2.5cm或6.5cm
过四点能否画圆
任意四个点是不是可以画一个圆?请举例说明.
不一定
四点在一条直线上不能作圆;
三点在同一直线上,另一点不在这条直线上不能做圆;
四点中任意三点不在一条直线可能作圆也可能做不出一个圆.
A
B
D
C
A
A
A
B
B
B
C
C
C
D
D
D
1.
2.
先确定圆心后计算
如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24cm,CD=8cm.
(1)求作此残片所在的圆
(
不写作法,保留作图痕迹
)
(2)求残片所在圆的面积.
答案:
(1)如图;(2)169π.
先确定圆心后计算
已知△ABC,
(1)请你用尺规作图作出△ABC的外接圆⊙O;
(2)若∠A=45°,
⊙O
的半径r=4,试求BC.
答案:
(1)如图;
(2)
总结
这节课我们学会了什么?
点和圆的位置关系:
设⊙O半径为r,点P到圆心的距离OP=d,则有:
点P在圆外
点P在圆上
点P在圆内
d>r
d=r
d<r
总结
这节课我们学会了什么?
不共线的三点确定一个圆:
?
?不在同一条直线上
的三个点确定一个圆.
三角形的外接圆:
过任意三角形的三个顶点都可以作一个唯一确定的圆.
这个圆心叫三角形的外心,
是三角形三边垂直平分线的交点.
总结
这节课我们学会了什么?
反证法:
不是直接从命题的已知得结论,
?而是假设命题的结论不成立??
由此经过推理的出矛盾,由矛盾判定假设不正确,
从而得到原命题成立,
这种方法叫做反证法.
点和圆的位置关系
我国射击运动员在奥运会上获金牌,为我国赢得荣誉,图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的.
你知道击中靶上不同位置的成绩是如何计算的吗?
解决这个问题就要研究点和圆的位置关系.
探究
问题1:观察,图中点A,点B,点C与圆的位置关系分别是什么?
问题2:设⊙O
半径为r,说出来点A,点B,点C
与圆心O
的距离与半径的关系.
点A在圆内
OA<r
点B在圆上
OB=r
点C在圆外
OC>r
探究
问题3:反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
OA<r
点A在圆内
OB=r
点B在圆上
OC>r
点C在圆外
归纳
设⊙O
半径为r,点P
到圆心的距离OP
=d,则有:
点P在圆外
d>r
点P在圆上
d=r
点P在圆内
d<r
这个符号读作“等价于”,它表示从该符号的左端可以推出右端,右端也能推出左端.
你知道击中靶上不同位置的成绩是如何计算的吗
?
射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域.
这些区域用由高到底的环数来表示,射击成绩
用弹着点位置对应的环数来表示.
弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.
例题
已知⊙O
的半径为10cm,A,B,C
三点到圆心O
的距离分别为8cm,10cm,12cm,则点A,B,C
与⊙O
的位置关系是:
点A在_________.
点B在_________.
点C在_________.
圆内
圆上
圆外
例题
如图所示,已知⊙O
和直线l,过圆心O
作OP⊥l,P
为垂足,A,B,C为直线l上三个点,且PA=2cm,PB
=3cm,PC
=4cm,若⊙O的半径为5cm,OP=4cm,判断A,B,C三点与⊙O的位置关系.
点A在_________.
点B在_________.
点C在_________.
圆内
圆上
圆外
例题
已知⊙O
的半径为
5,圆心
O
的坐标为(0,0),若点
P
的坐标为(4,2),点
P
与⊙O
的位置关系是____________________.
由勾股定理可知,
所以
点P在⊙O内
练习
已知⊙O
的半径为4,OP=3.4,则P
在⊙O
的________.
内部
练习
已知
点P
在
⊙O
的外部,OP=5,那么⊙O
的半径r满足_____________.
0<r<5
练习
已知⊙O
的半径为5,M
为ON的中点,当OM=3时,N点与⊙O
的位置关系是N
在⊙O
的_____________.
外部
练习
⊙O
直径为d,点A到圆心的距离为m,若点
A不在圆
外,则d与m的关系是_____________.
练习
有一张矩形纸片,AB
=3cm,AD
=4cm,若以A为圆心作圆,并且要使点D
在⊙A内,而点C
在⊙A外,
⊙A的半径
r
的取值范围是__________________.
补充题
⊙O
的半径为
5
cm,O
到直线l的距离OP=3cm,Q
为l上一点且PQ
=4.2cm,点Q
在⊙O
_________.
外
补充题
如图,
数轴上半径为1的⊙O
从原点O
开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P
以每秒2个单位的速度向左运动,经过_________秒后,点P在⊙O
上.
2或
我们知道,已知______和_______,可以确定一个圆.
问题1:经过一个已知点A能不能作圆,能作多少个圆?
能作无数个圆
A
圆心
半径
过一个点作圆
.
我们知道,已知______和_______,可以确定一个圆.
问题2:经过两个已知点A,B,能不能作圆?
圆心有什么特点?
由于圆心到A,B
的距离相等,
所以圆心在线段AB
的垂直平分线上.
圆心
半径
A
B
过两个点作圆
探究
总结:过已知点作圆,关键就是确定______.
问题3:经过不在同一直线上的三个点A,B,C
能不能作圆?如果能,怎么确定圆心?
圆心
圆心O到A,B,C
的距离都相等
所以O
既在线段AB
的垂直平分线上
又在线段BC
的垂直平分线上
垂直平分线的交点就是圆心O
以O为圆心,OA(
或OB,OC
)为半径作圆即为所求.
B
C
A
O
问题4:经过不在同一直线上的三个点A,B,C
能作几个圆?
由于圆心O是唯一确定的,
所以圆也是唯一确定的.
?
?不在同一条直线上
的三个点确定一个圆.
过三个点作圆
因为
?不在同一条直线上
的三个点确定一个圆.
所以
经过三角形的三个顶点一定可以作一个圆.
这个圆叫做三角形的外接圆.
外接圆的圆心是三角形三条边的_______________的交点,
叫做三角形的外心.
垂直平分线
三角形的外接圆
例题
一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
答案:关键就是确定圆心.
圆弧边缘任取三个点,
然后连接其中任意两组点,作它们的垂直平分线,
所得交点就是圆心,
进而可以画出整个圆.
练习
直角三角形的外心是______的中点,
锐角三角形的外心在三角形______,
钝角三角形的外心在三角形_______.
斜边
内部
外部
练习
三角形的外心具有的性质是
(?
?
?
?)
A.到三个顶点的距离相等
B.到三边的距离相等
C.是三角形三条角平分线的交点
D.是三角形三条中线的交点
A
练习
下列命题中不正确的是
(?
?
?
?)
A.圆有且只有一个内接三角形
B.三角形只有一个外接圆
C.三角形的外心是这个三角形任意两边的垂直平分线的交点
D.等边三角形的外心也是三角形的三条中线、高、角平分线的交点
A
练习
判断:
1.经过三点一定可以作圆.(?
?
?
)
2.三角形的外心就是这个三角形两边垂直平分线
的交点.(?
?
?)
3.三角形的外心到三边的距离相等.(?
?
?
)
练习
如图,黑猫警长发现一只老鼠溜进了一个内部连通的鼠洞,鼠洞只有三个出口A,B,C.要想同时顾及这三个出口以防老鼠出洞,黑猫警长最好蹲守在(?
?
?)
A.△ABC
的三边高线的交点P处
B.
△ABC
的三角平分线的交点P处
C.
△ABC
的三边中线的交点P处
D.
△ABC
的三边中垂线的交点P处
D
补充题
若
A、B、C
为平面上的三点,
AB
=2,BC
=3,AC
=5,
则(?
?
?)
D
A.可以画一个圆,使A,B,C
都在圆周上
B
.可以画一个圆,使A,B
在圆周上,C
在圆内
C
.可以画一个圆,使A,C
在圆周上,B
在圆外
D
.可以画一个圆,使A,C
在圆周上,B
在圆内
思考
经过同一条直线上的三个点能作出一个圆吗?
如图,假设过同一条直线l上三点A、B、C
可以做一个圆,设这个圆的圆心为P,
那么点P既在线段AB
的垂直平分线l?
上,
又在线段BC
的垂直平分线l?
上,
即点P
为l?
与l?
的交点.
讨论一下:你们能发现什么不对劲的地方吗?
P
思考
经过同一条直线上的三个点能作出一个圆吗?
如图,假设过同一条直线l上三点A、B、C
可以做一个圆,设这个圆的圆心为P,
l?
⊥l,l?
⊥l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直相矛盾,
假设不成立,所以过同一条直线上的三点不能做圆.
反证法
上面的证明“过同一条直线上的三点不能做圆”的方法与我们以前学过的证明不同,
它不是直接从命题的已知得结论,?
?
?
?
?而是假设命题的结论不成立
由此经过推理的出矛盾,由矛盾判定假设不正确,
从而得到原命题成立,
这种方法叫做反证法.
用反证法证明平行线的性质“两直线平行,同位角相等”.
已知AB∥CD,求证:∠1=∠2.
假设∠1≠∠2,过点O
作A’B’,
使∠EOB’=∠2.
根据“同位角相等,两直线平行”,
可得A’B’∥CD.
由此可知,过点O
的直线AB和直线A’B’都与直线CD平行.
讨论一下,你们能发现矛盾之处吗?
平行线性质定理的证明
用反证法证明平行线的性质“两直线平行,同位角相等”.
已知AB∥CD,求证:∠1=∠2.
由此可知,过点O
的直线AB
和直线A’B’都与直线CD
平行.
这与平行公理“过直线外一点有且只有一条直线与已知直线平行”矛盾.
这说明假设∠1≠∠2不正确,
从而∠1=∠2.
平行线性质定理的证明
练习
画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
练习
体育课上,小明和小雨的铅球成绩分别是6.4m和5.1m,他们投出的铅球分别落在图中哪个区域内.
练习
如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.
在⊙O
中,点M
到⊙O的最小距离为3,最大距离是19,那么⊙O
的半径为__________.
11或8
点到圆的距离最值
点到圆的距离最值
一个点与定圆上最近点的距离为
4
cm,最远点的距离为
9
cm,则此圆的半径为________________.
2.5cm或6.5cm
过四点能否画圆
任意四个点是不是可以画一个圆?请举例说明.
不一定
四点在一条直线上不能作圆;
三点在同一直线上,另一点不在这条直线上不能做圆;
四点中任意三点不在一条直线可能作圆也可能做不出一个圆.
A
B
D
C
A
A
A
B
B
B
C
C
C
D
D
D
1.
2.
先确定圆心后计算
如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24cm,CD=8cm.
(1)求作此残片所在的圆
(
不写作法,保留作图痕迹
)
(2)求残片所在圆的面积.
答案:
(1)如图;(2)169π.
先确定圆心后计算
已知△ABC,
(1)请你用尺规作图作出△ABC的外接圆⊙O;
(2)若∠A=45°,
⊙O
的半径r=4,试求BC.
答案:
(1)如图;
(2)
总结
这节课我们学会了什么?
点和圆的位置关系:
设⊙O半径为r,点P到圆心的距离OP=d,则有:
点P在圆外
点P在圆上
点P在圆内
d>r
d=r
d<r
总结
这节课我们学会了什么?
不共线的三点确定一个圆:
?
?不在同一条直线上
的三个点确定一个圆.
三角形的外接圆:
过任意三角形的三个顶点都可以作一个唯一确定的圆.
这个圆心叫三角形的外心,
是三角形三边垂直平分线的交点.
总结
这节课我们学会了什么?
反证法:
不是直接从命题的已知得结论,
?而是假设命题的结论不成立??
由此经过推理的出矛盾,由矛盾判定假设不正确,
从而得到原命题成立,
这种方法叫做反证法.
同课章节目录
