人教版八年级上册 数学 课件: 11.2.2三角形的外角(共20张PPT)
文档属性
| 名称 | 人教版八年级上册 数学 课件: 11.2.2三角形的外角(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 520.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
11.2.2三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=20
°
,则∠B=
;
(2)∠A=40
°
,∠B=∠C,则∠B=
.
1、三角形三个内角的和等于多少度?
知识回顾
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A= ,
∠B=
∠C=
40°
60°
80°
70°
70°
三角形的内角和等于180度
咦,这哥俩怎么了?
三角形都长头发了
谁让你光注意三角形的里边呢
外边还有啥?
还有一个角呢!
A
B
C
D
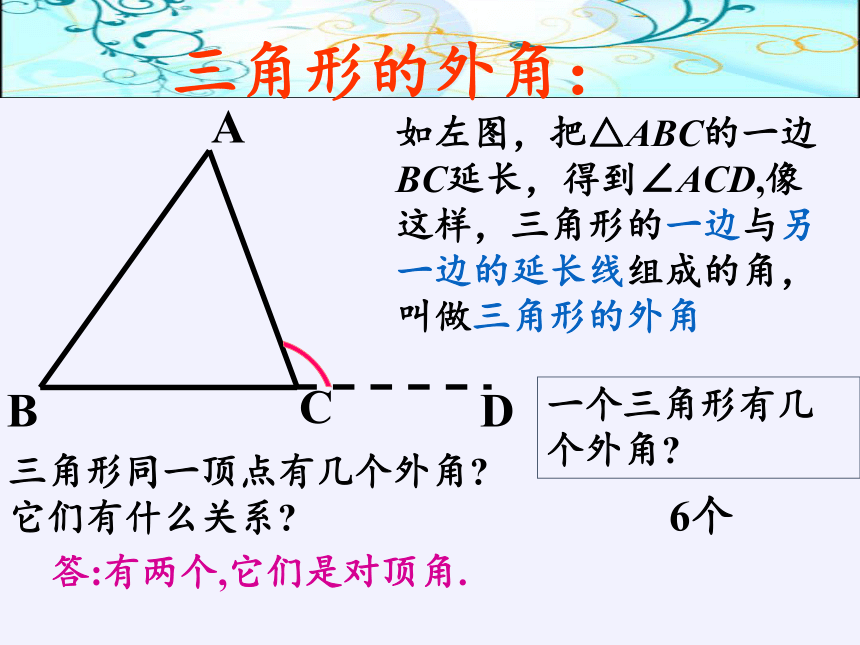
三角形的外角:
如左图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角
一个三角形有几个外角?
6个
三角形同一顶点有几个外角?
它们有什么关系?
答:有两个,它们是对顶角.
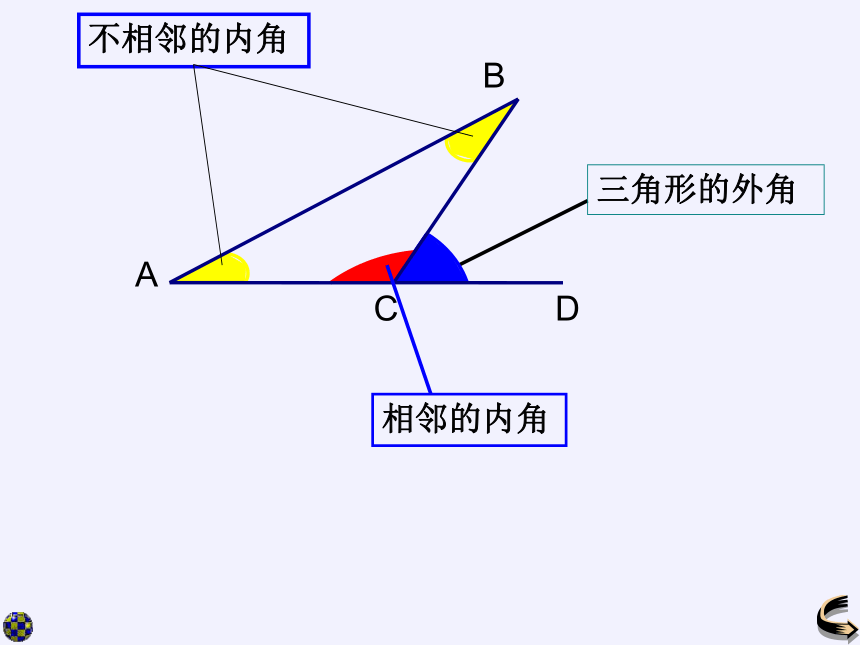
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
A
B
C
D
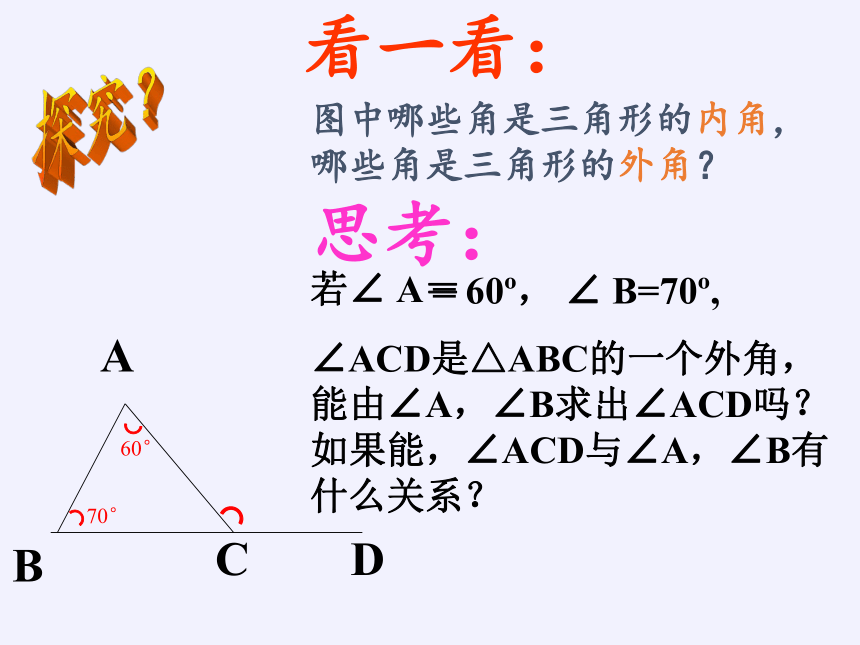
看一看:
思考:
若∠
A=
60?,
∠
B=70?,
∠ACD是△ABC的一个外角,能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有
什么关系?
探究?
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
60°
70°
=
通过上题的计算,任意一个三角形的外角与他不相邻的两个内角是否都有这种关系?请你试着用自己的语言说一说.
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
结论:
三角形外角性质
D
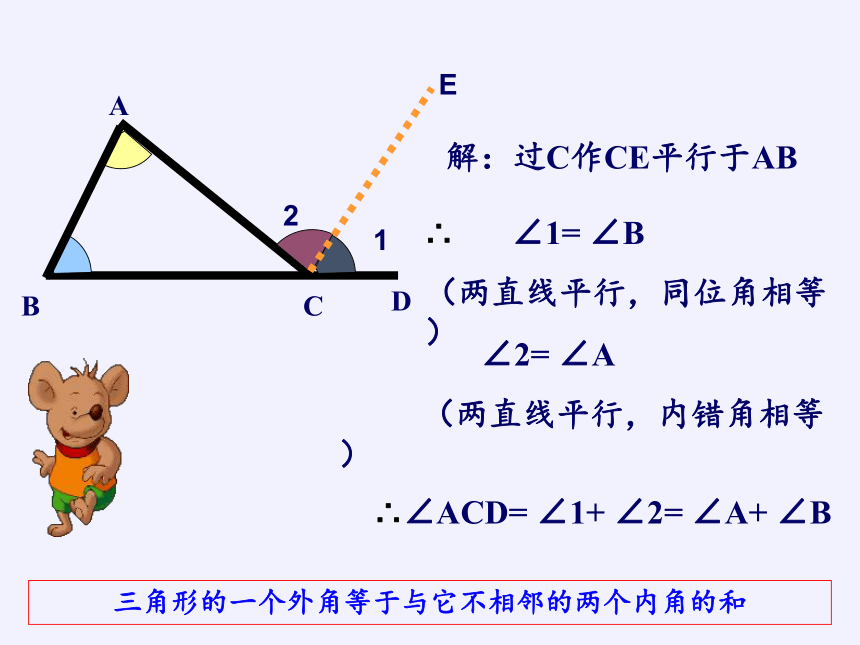
解:过C作CE平行于AB
A
B
C
1
2
∴
∠1=
∠B
(两直线平行,同位角相等)
∠2=
∠A
(两直线平行,内错角相等)
∴∠ACD=
∠1+
∠2=
∠A+
∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
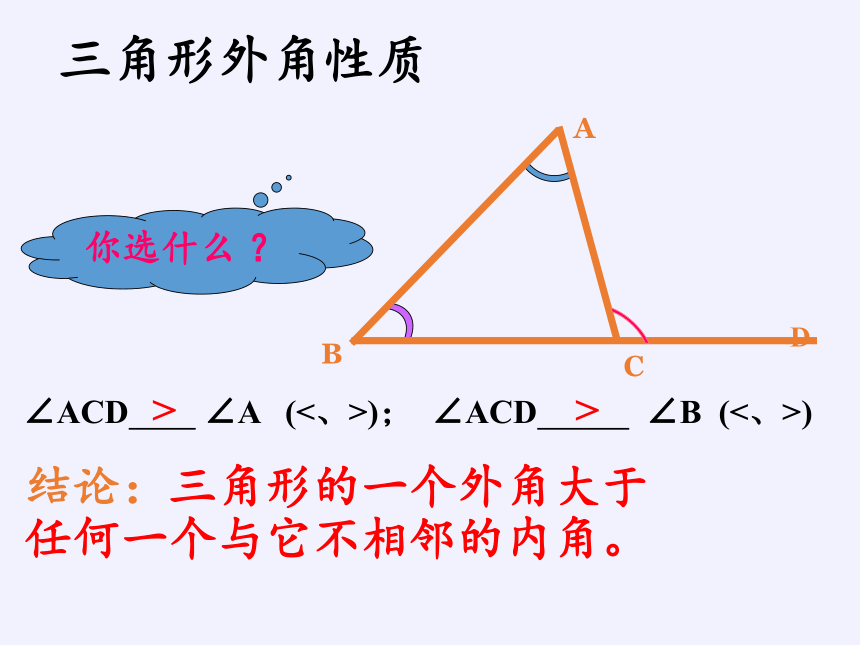
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
你选什么
?
三角形外角性质
三角形外角的性质:
1、三角形的一个外角等于
与它不相邻的两个内角的
和。
∠B+∠C=∠CAD
2、三角形的一个外角大于任何
一个与它不相邻的内角。
∠CAD
>
∠B,
∠CAD
>
∠C
A
B
C
D
求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90?
85?
95?
180-30-60
120-35
45+50
把图中∠1、
∠2、
∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
三角形的一个外角大于任何一个与它不相邻的内角。
练一练
已知图中∠A、
∠B、
∠C分别为80°,
20°
,
30°
,求∠1的度数
B
3
2
1
A
C
D
E
∠2=110°
∠1=130°
探究与交流:
三角形每个顶点处分别有两个外角,如果每个处各取一个外角,那么这三个外角的和就叫做三角形的外角和。请同学们小组交流探究出三角形的外角和是多少?
A
B
C
1
2
3
∠1+
∠2+
∠3=?
A
B
C
1
2
3
方法1
方法2
三角形的外角和360°
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果
理论研讨
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的外角和等于它内角和的2倍。(
)
3、三角形的一个外角等于两个内角的和。(
)
4、三角形的一个外角等于与它不相邻的两个内角的和。(
)
5、三角形的一个外角大于任何一个内角。(
)
6、三角形的一个内角小于任何一个与它不相邻的外角。(
)
小结
1、三角形的两个性质
①
三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它不相邻的内角。
2、三角形的外角和360°
作业:
课本P16页
复习巩固第3,4,5题
谢
谢
11.2.2三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=20
°
,则∠B=
;
(2)∠A=40
°
,∠B=∠C,则∠B=
.
1、三角形三个内角的和等于多少度?
知识回顾
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A= ,
∠B=
∠C=
40°
60°
80°
70°
70°
三角形的内角和等于180度
咦,这哥俩怎么了?
三角形都长头发了
谁让你光注意三角形的里边呢
外边还有啥?
还有一个角呢!
A
B
C
D
三角形的外角:
如左图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角
一个三角形有几个外角?
6个
三角形同一顶点有几个外角?
它们有什么关系?
答:有两个,它们是对顶角.
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
A
B
C
D
看一看:
思考:
若∠
A=
60?,
∠
B=70?,
∠ACD是△ABC的一个外角,能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有
什么关系?
探究?
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
60°
70°
=
通过上题的计算,任意一个三角形的外角与他不相邻的两个内角是否都有这种关系?请你试着用自己的语言说一说.
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
结论:
三角形外角性质
D
解:过C作CE平行于AB
A
B
C
1
2
∴
∠1=
∠B
(两直线平行,同位角相等)
∠2=
∠A
(两直线平行,内错角相等)
∴∠ACD=
∠1+
∠2=
∠A+
∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
你选什么
?
三角形外角性质
三角形外角的性质:
1、三角形的一个外角等于
与它不相邻的两个内角的
和。
∠B+∠C=∠CAD
2、三角形的一个外角大于任何
一个与它不相邻的内角。
∠CAD
>
∠B,
∠CAD
>
∠C
A
B
C
D
求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90?
85?
95?
180-30-60
120-35
45+50
把图中∠1、
∠2、
∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
三角形的一个外角大于任何一个与它不相邻的内角。
练一练
已知图中∠A、
∠B、
∠C分别为80°,
20°
,
30°
,求∠1的度数
B
3
2
1
A
C
D
E
∠2=110°
∠1=130°
探究与交流:
三角形每个顶点处分别有两个外角,如果每个处各取一个外角,那么这三个外角的和就叫做三角形的外角和。请同学们小组交流探究出三角形的外角和是多少?
A
B
C
1
2
3
∠1+
∠2+
∠3=?
A
B
C
1
2
3
方法1
方法2
三角形的外角和360°
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果
理论研讨
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的外角和等于它内角和的2倍。(
)
3、三角形的一个外角等于两个内角的和。(
)
4、三角形的一个外角等于与它不相邻的两个内角的和。(
)
5、三角形的一个外角大于任何一个内角。(
)
6、三角形的一个内角小于任何一个与它不相邻的外角。(
)
小结
1、三角形的两个性质
①
三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它不相邻的内角。
2、三角形的外角和360°
作业:
课本P16页
复习巩固第3,4,5题
谢
谢
