人教版八年级上册 数学 课件: 14.1.2幂的乘方(共22张PPT)
文档属性
| 名称 | 人教版八年级上册 数学 课件: 14.1.2幂的乘方(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 265.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 13:13:50 | ||
图片预览






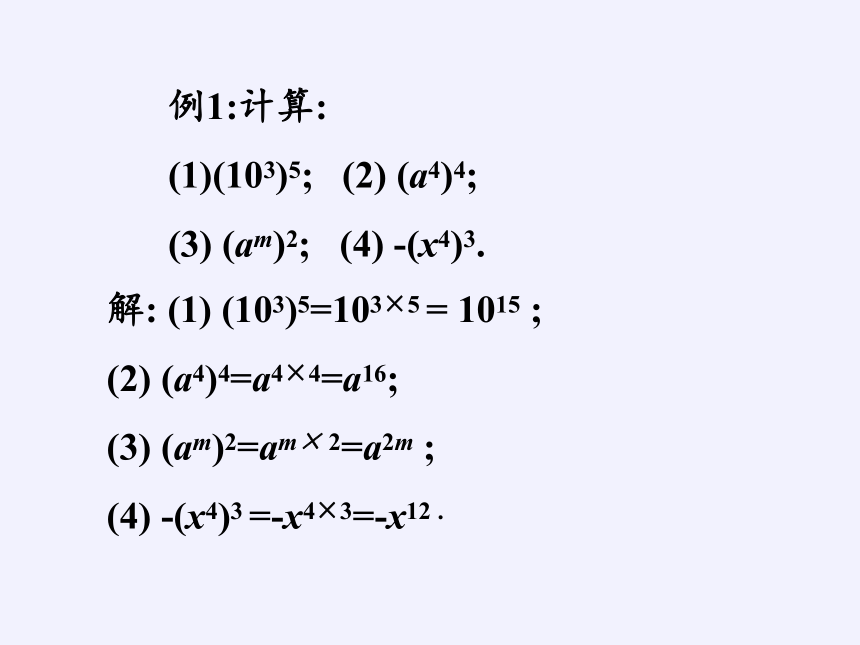


文档简介
(共22张PPT)
14.1.2幂的乘方
1.口述同底数幂的乘法法则.
2.下面的计算对不对?如果不对应该怎样改正?
⑴
⑵
⑶
3.计算:
知识回顾:
思考:如果正方体的棱长是b2cm,那么这个正方体的体积是(
)cm3
(b2)3
式子(b2)3由括号内
与括号外两部分构成
⑴
⑵
⑶
(m是正整数).
3.根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:
2.
你发现了什么?
1.试一试:读出式子
探究
6
6
3m
(根据
)
乘方的意义
(根据
)
同底数幂的乘法法则
(根据乘法的定义)
对于任意底数a与任意正整数m,n,
(乘方的意义)
(同底数幂的乘法法则)
(乘法的定义)
(m,n都是正整数).
幂的乘方,底数
,指数
.
不变
相乘
n个am
=am+m+m+…m
n个m
例1:计算:
(103)5;
(2)
(a4)4;
(3)
(am)2;
(4)
-(x4)3.
解:
(1)
(103)5=103×5
=
1015
;
(2)
(a4)4=a4×4=a16;
(3)
(am)2=am×
2=a2m
;
(4)
-(x4)3
=-x4×3=-x12
.
相信你准能做对哟
变式计算:
(2)
例2
计算:
a2·a4+(a3)2
解:原式=a2+4+a3×2
=a6+a6
=2a6
例3:把[(x+y)2]4化成(x+y)n的形式
解:
[(x+y)2]4=(x+y)2×4=(x+y)8
例4:已知,44×83=2x,求x的值.
实践与创新
解:
幂的乘方与同底数幂的乘法的异同:
相同点是:
不同点是:
都是底数不变
同底数幂的乘法是指数相加;
而幂的乘方是指数相乘.
能否利用幂的乘方法则来进行计算呢?
公式中的a可代表一个数、字母、式子等.
幂的乘方法则的逆用
(m,n都是正整数).
例5:a2m=2,b3n=3,求(a3m)2-(b2n)3的值
解:(a3m)2-(b2n)3
=a6m-b6n
=(a2m)3-(b3n)2
=(2)3-(3)2
=8-9
=-1
=a2m·3-b3n·2
幂的乘方法则的逆用
已知10a=5,10b=6,求103a+2b的值.
解:4
500
变式计算:
运算总结:
当幂的指数是加法时,可变为_____________
当幂的指数是乘法时,可变为_____________
幂的乘方法则的逆用
同底数幂的乘法
幂的乘方
一、选择题
1.a12不能写成( )
A.(a3)4
B.(a6)2
C.(a2)10
D.a2·a10
2.下列计算中正确的是( )
A.(-an)2=an+2
B.(-a3)4=(-a4)3
C.(a4)4=a4·a
D.(a4)4=(a2)8
3.下列式子中与a3m+1一定相等的是( )
A.(am+1)3
B.(a3)m+1
C.a·(a3)m
D.a·a2·am
C
D
C
课堂练习
二、填空题
4.若x5·(xm)3=x11,则m=____.
5.已知64×83=2x,则x=____.
2
15
小结
同底数幂乘法法则:
am·an=am+n(m,n都是正整数)
底数
,
指数
.
幂的乘方的法则:
(am)n
=
amn
(m,n
都是正整数).
底数
,
指数
.
相加
相乘
不变
不变
幂的意义
小结
运算总结:
当幂的指数是加法时,可变为____________
当幂的指数是乘法时,可变为_____________
同底数幂的乘法
幂的乘方
课后思考题.
比较255,344,433
的大小.
谢
谢
14.1.2幂的乘方
1.口述同底数幂的乘法法则.
2.下面的计算对不对?如果不对应该怎样改正?
⑴
⑵
⑶
3.计算:
知识回顾:
思考:如果正方体的棱长是b2cm,那么这个正方体的体积是(
)cm3
(b2)3
式子(b2)3由括号内
与括号外两部分构成
⑴
⑵
⑶
(m是正整数).
3.根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:
2.
你发现了什么?
1.试一试:读出式子
探究
6
6
3m
(根据
)
乘方的意义
(根据
)
同底数幂的乘法法则
(根据乘法的定义)
对于任意底数a与任意正整数m,n,
(乘方的意义)
(同底数幂的乘法法则)
(乘法的定义)
(m,n都是正整数).
幂的乘方,底数
,指数
.
不变
相乘
n个am
=am+m+m+…m
n个m
例1:计算:
(103)5;
(2)
(a4)4;
(3)
(am)2;
(4)
-(x4)3.
解:
(1)
(103)5=103×5
=
1015
;
(2)
(a4)4=a4×4=a16;
(3)
(am)2=am×
2=a2m
;
(4)
-(x4)3
=-x4×3=-x12
.
相信你准能做对哟
变式计算:
(2)
例2
计算:
a2·a4+(a3)2
解:原式=a2+4+a3×2
=a6+a6
=2a6
例3:把[(x+y)2]4化成(x+y)n的形式
解:
[(x+y)2]4=(x+y)2×4=(x+y)8
例4:已知,44×83=2x,求x的值.
实践与创新
解:
幂的乘方与同底数幂的乘法的异同:
相同点是:
不同点是:
都是底数不变
同底数幂的乘法是指数相加;
而幂的乘方是指数相乘.
能否利用幂的乘方法则来进行计算呢?
公式中的a可代表一个数、字母、式子等.
幂的乘方法则的逆用
(m,n都是正整数).
例5:a2m=2,b3n=3,求(a3m)2-(b2n)3的值
解:(a3m)2-(b2n)3
=a6m-b6n
=(a2m)3-(b3n)2
=(2)3-(3)2
=8-9
=-1
=a2m·3-b3n·2
幂的乘方法则的逆用
已知10a=5,10b=6,求103a+2b的值.
解:4
500
变式计算:
运算总结:
当幂的指数是加法时,可变为_____________
当幂的指数是乘法时,可变为_____________
幂的乘方法则的逆用
同底数幂的乘法
幂的乘方
一、选择题
1.a12不能写成( )
A.(a3)4
B.(a6)2
C.(a2)10
D.a2·a10
2.下列计算中正确的是( )
A.(-an)2=an+2
B.(-a3)4=(-a4)3
C.(a4)4=a4·a
D.(a4)4=(a2)8
3.下列式子中与a3m+1一定相等的是( )
A.(am+1)3
B.(a3)m+1
C.a·(a3)m
D.a·a2·am
C
D
C
课堂练习
二、填空题
4.若x5·(xm)3=x11,则m=____.
5.已知64×83=2x,则x=____.
2
15
小结
同底数幂乘法法则:
am·an=am+n(m,n都是正整数)
底数
,
指数
.
幂的乘方的法则:
(am)n
=
amn
(m,n
都是正整数).
底数
,
指数
.
相加
相乘
不变
不变
幂的意义
小结
运算总结:
当幂的指数是加法时,可变为____________
当幂的指数是乘法时,可变为_____________
同底数幂的乘法
幂的乘方
课后思考题.
比较255,344,433
的大小.
谢
谢
