人教版八年级数学上册同步练习题: 12.3角的平分线的性质(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册同步练习题: 12.3角的平分线的性质(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 284.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 00:00:00 | ||
图片预览



文档简介
人教版八年级数学上册同步练习题
第十二章全等三角形
12.3角的平分线的性质
一、单选题
1.已知∠AOB,求作射线OC,使OC平分∠AOB.①画射线OC即为所求;②以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;③分别以点M、N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C,则上面作法的合理顺序为(
).
A.②③①
B.③①②
C.③②①
D.②①③
2.作已知角的平分线是根据三角形的全等判定( )作的.
A.AAS
B.ASA
C.SAS
D.SSS
3.如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12
cm,则△DBE的周长为(
)
A.12
cm
B.11
cm
C.14
cm
D.10
cm
4.给出下列结论,正确的有(
).
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个
B.2个
C.3个
D.4个
5.已知△ABC的周长是60cm,三条角平分线交于P点,且P点到BC的距离是10cm,则△ABC的面积为
( )
A.600?cm2
B.300?cm2
C.300?cm2
D.无法确定
6.直线AB上有一点O,射线OD和射线OC在AB同侧,,,则与的平分线的夹角的度数是
A.
B.
C.
D.以上都不对
7.三角形内有一点,它到三角形三边的距离都相等,同时与三角形三个顶点的距离也相等,则这个三角形一定是(
)
A.等腰三角形
B.等腰直角三角形
C.等边三角形
D.以上都不对
8.在△ABC中,∠ACB=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F是垂足,且AB=5,BC=4,AC=3,则点O到三边AB,AC,BC的距离分别是(
)
A.1,1,1
B.2,2,2
C.1,1.5,2
D.无法确定
9.已知一个等腰三角形的一边长为5,另一边长为7,则这个等腰三角形的周长为(
)
A.12
B.17
C.17或19
D.19
10.已知,△ABC的三边AB,BC,AC的长分别是40,50,60,△ABC三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=(
)
A.2:3:4
B.4:5:6
C.3:4:5
D.1:2:3
二、填空题
11.点O是△ABC内一点,且点O到三边的距离相等,∠A=50°,则∠BOC=
.
12.利用直尺和圆规作出一个角的角平分线的作法,其理论依据是全等三角形判定方法________?.
13.△ABC中,∠C=90°,AD平分∠BAC交BC于D,且BD:CD=3:2,BC=15cm,则点D到AB的距离是__________。
14.已知AOB是直角,OM平分BOC,ON平分AOC,那么MON=___________。
15.一条射线把一个角分成两个角,这条射线叫这个角的平分线.(_____)
三、解答题
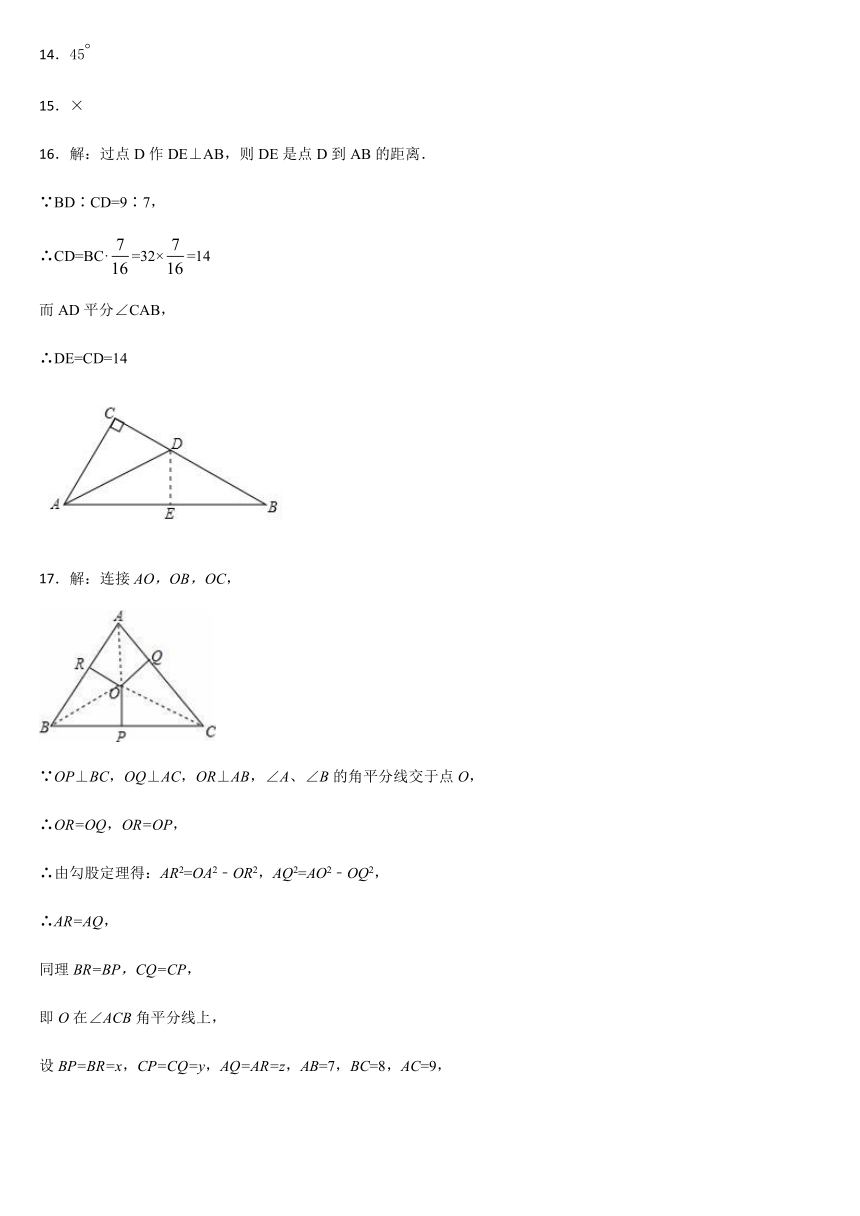
16.已知:如下图在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若BC=32,且BD∶CD=9∶7,求:D到AB边的距离.
17.如图.已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
(1)求BP、CQ、AR的长.
(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.
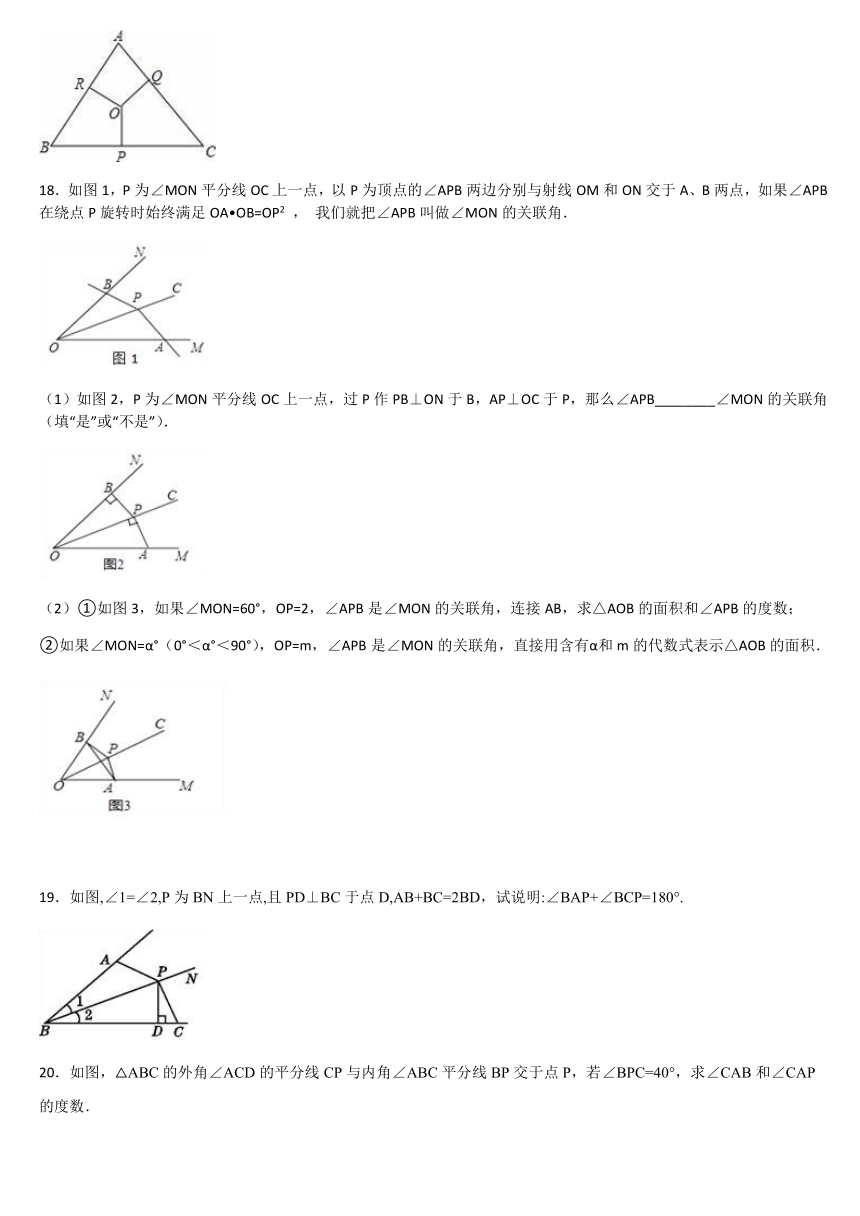
18.如图1,P为∠MON平分线OC上一点,以P为顶点的∠APB两边分别与射线OM和ON交于A、B两点,如果∠APB在绕点P旋转时始终满足OA?OB=OP2
,
我们就把∠APB叫做∠MON的关联角.
(1)如图2,P为∠MON平分线OC上一点,过P作PB⊥ON于B,AP⊥OC于P,那么∠APB________∠MON的关联角(填“是”或“不是”).
(2)①如图3,如果∠MON=60°,OP=2,∠APB是∠MON的关联角,连接AB,求△AOB的面积和∠APB的度数;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的关联角,直接用含有α和m的代数式表示△AOB的面积.
19.如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD,试说明:∠BAP+∠BCP=180°.
20.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB和∠CAP的度数.
21.在△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠EAF=180°,求证DE=DF.
22.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
23.如图,已知用尺规将一个任意角三等分是不可能的,但对于一些特殊角则可以利用作等边三角形的方法三等分,请用直尺和圆规把平角和这两个角三等分(尺规作图,要求保留作图痕迹,不必写出作法)
【参考答案】
1.A
2.D
3.A
4.A
5.B
6.C
7.C
8.A
9.C
10.B
11.115°.
12.SSS
13.6cm
14.45
15.×
16.解:过点D作DE⊥AB,则DE是点D到AB的距离.
∵BD∶CD=9∶7,
∴CD=BC·=32×=14
而AD平分∠CAB,
∴DE=CD=14
17.解:连接AO,OB,OC,
∵OP⊥BC,OQ⊥AC,OR⊥AB,∠A、∠B的角平分线交于点O,
∴OR=OQ,OR=OP,
∴由勾股定理得:AR2=OA2﹣OR2,AQ2=AO2﹣OQ2,
∴AR=AQ,
同理BR=BP,CQ=CP,
即O在∠ACB角平分线上,
设BP=BR=x,CP=CQ=y,AQ=AR=z,AB=7,BC=8,AC=9,
则,
x=3,y=5,z=4,
∴BP=3,CQ=5,AR=4.
(2)过O作OM⊥AC于M,ON⊥AB于N,
∵O在∠A的平分线,
∴OM=ON,∠ANO=∠AMO=90°,
∵∠A=60°,
∴∠NOM=120°,
∵O在∠ACB、∠ABC的角平分线上,
∴∠EBC+∠FCB=(∠ABC+∠ACB)=×(180°﹣∠A)=60°,
∴∠FON=∠EOM,
在△FON和△EOM中,
∠ONF=∠OME,ON=OM,∠FON=∠EOM,
∴△FON≌△EOM,
∴OE=OF.
18.略
19.证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,PD=PE,BP=BP,
∴△BPD≌△BPE.
∴BE=BD.
∵AB+BC=2BD,BC=BD+DC,AB=BE-AE,
∴AE=CD.
∵PD=PE,AE=CD,PD⊥BC,PE⊥BM,
∴△PCD≌△PAE,
∴∠PCB=∠PAE.
∵∠BAP+∠PAE=180°,
∴∠BAP+∠PCB=180°.
20.解:如图所示:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
设∠PCD
=
x°
∵CP平分∠
ACD
∴∠ACP
=∠PCD
=
x°,PM=PN
∵BP平分∠
ABC
∴∠ABP=∠PBC,PF=PN
∴PM=PF
∵∠BPC=40°
∴∠ABP=∠PBC=∠PCD?∠BPC=(x?40)°
∴∠CAB=∠ACD?∠ABC=2x°?2(x?40)°=80°
∵PM=PF,AP=AP,PF⊥BA,PM⊥AC
∴Rt△PAF
≌
Rt
△PAM
∴∠CAP=∠PAF=(180°?∠CAB)=
(180°?80°)=50°
故本题答案应为:∠CAB=80°,∠CAP=50°
21.证明:过D作DM⊥AB于M,DN⊥AC于N,
即∠EMD=∠FND=90°,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN(角平分线性质),
∵∠EAF+∠EDF=180°,
∴∠MED+∠AFD=360°-180°=180°,
∵∠AFD+∠NFD=180°,
∴∠MED=∠NFD,
在△EMD和△FND中
,
∴△EMD≌△FND(AAS),
∴DE=DF.
22.(1)证明:连接BD,CD,
∵
AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,解得:x=1,
∴BE=1,即AE=AB﹣BE=5﹣1=4.
23.解:如图所示,射线、为平角的三等分线;
如图所示,射线、为的三等分线.
第十二章全等三角形
12.3角的平分线的性质
一、单选题
1.已知∠AOB,求作射线OC,使OC平分∠AOB.①画射线OC即为所求;②以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;③分别以点M、N为圆心,大于MN的长为半径画弧,两弧在∠AOB的内部相交于点C,则上面作法的合理顺序为(
).
A.②③①
B.③①②
C.③②①
D.②①③
2.作已知角的平分线是根据三角形的全等判定( )作的.
A.AAS
B.ASA
C.SAS
D.SSS
3.如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12
cm,则△DBE的周长为(
)
A.12
cm
B.11
cm
C.14
cm
D.10
cm
4.给出下列结论,正确的有(
).
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个
B.2个
C.3个
D.4个
5.已知△ABC的周长是60cm,三条角平分线交于P点,且P点到BC的距离是10cm,则△ABC的面积为
( )
A.600?cm2
B.300?cm2
C.300?cm2
D.无法确定
6.直线AB上有一点O,射线OD和射线OC在AB同侧,,,则与的平分线的夹角的度数是
A.
B.
C.
D.以上都不对
7.三角形内有一点,它到三角形三边的距离都相等,同时与三角形三个顶点的距离也相等,则这个三角形一定是(
)
A.等腰三角形
B.等腰直角三角形
C.等边三角形
D.以上都不对
8.在△ABC中,∠ACB=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F是垂足,且AB=5,BC=4,AC=3,则点O到三边AB,AC,BC的距离分别是(
)
A.1,1,1
B.2,2,2
C.1,1.5,2
D.无法确定
9.已知一个等腰三角形的一边长为5,另一边长为7,则这个等腰三角形的周长为(
)
A.12
B.17
C.17或19
D.19
10.已知,△ABC的三边AB,BC,AC的长分别是40,50,60,△ABC三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=(
)
A.2:3:4
B.4:5:6
C.3:4:5
D.1:2:3
二、填空题
11.点O是△ABC内一点,且点O到三边的距离相等,∠A=50°,则∠BOC=
.
12.利用直尺和圆规作出一个角的角平分线的作法,其理论依据是全等三角形判定方法________?.
13.△ABC中,∠C=90°,AD平分∠BAC交BC于D,且BD:CD=3:2,BC=15cm,则点D到AB的距离是__________。
14.已知AOB是直角,OM平分BOC,ON平分AOC,那么MON=___________。
15.一条射线把一个角分成两个角,这条射线叫这个角的平分线.(_____)
三、解答题
16.已知:如下图在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若BC=32,且BD∶CD=9∶7,求:D到AB边的距离.
17.如图.已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
(1)求BP、CQ、AR的长.
(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.
18.如图1,P为∠MON平分线OC上一点,以P为顶点的∠APB两边分别与射线OM和ON交于A、B两点,如果∠APB在绕点P旋转时始终满足OA?OB=OP2
,
我们就把∠APB叫做∠MON的关联角.
(1)如图2,P为∠MON平分线OC上一点,过P作PB⊥ON于B,AP⊥OC于P,那么∠APB________∠MON的关联角(填“是”或“不是”).
(2)①如图3,如果∠MON=60°,OP=2,∠APB是∠MON的关联角,连接AB,求△AOB的面积和∠APB的度数;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的关联角,直接用含有α和m的代数式表示△AOB的面积.
19.如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD,试说明:∠BAP+∠BCP=180°.
20.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB和∠CAP的度数.
21.在△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠EAF=180°,求证DE=DF.
22.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
23.如图,已知用尺规将一个任意角三等分是不可能的,但对于一些特殊角则可以利用作等边三角形的方法三等分,请用直尺和圆规把平角和这两个角三等分(尺规作图,要求保留作图痕迹,不必写出作法)
【参考答案】
1.A
2.D
3.A
4.A
5.B
6.C
7.C
8.A
9.C
10.B
11.115°.
12.SSS
13.6cm
14.45
15.×
16.解:过点D作DE⊥AB,则DE是点D到AB的距离.
∵BD∶CD=9∶7,
∴CD=BC·=32×=14
而AD平分∠CAB,
∴DE=CD=14
17.解:连接AO,OB,OC,
∵OP⊥BC,OQ⊥AC,OR⊥AB,∠A、∠B的角平分线交于点O,
∴OR=OQ,OR=OP,
∴由勾股定理得:AR2=OA2﹣OR2,AQ2=AO2﹣OQ2,
∴AR=AQ,
同理BR=BP,CQ=CP,
即O在∠ACB角平分线上,
设BP=BR=x,CP=CQ=y,AQ=AR=z,AB=7,BC=8,AC=9,
则,
x=3,y=5,z=4,
∴BP=3,CQ=5,AR=4.
(2)过O作OM⊥AC于M,ON⊥AB于N,
∵O在∠A的平分线,
∴OM=ON,∠ANO=∠AMO=90°,
∵∠A=60°,
∴∠NOM=120°,
∵O在∠ACB、∠ABC的角平分线上,
∴∠EBC+∠FCB=(∠ABC+∠ACB)=×(180°﹣∠A)=60°,
∴∠FON=∠EOM,
在△FON和△EOM中,
∠ONF=∠OME,ON=OM,∠FON=∠EOM,
∴△FON≌△EOM,
∴OE=OF.
18.略
19.证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,PD=PE,BP=BP,
∴△BPD≌△BPE.
∴BE=BD.
∵AB+BC=2BD,BC=BD+DC,AB=BE-AE,
∴AE=CD.
∵PD=PE,AE=CD,PD⊥BC,PE⊥BM,
∴△PCD≌△PAE,
∴∠PCB=∠PAE.
∵∠BAP+∠PAE=180°,
∴∠BAP+∠PCB=180°.
20.解:如图所示:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
设∠PCD
=
x°
∵CP平分∠
ACD
∴∠ACP
=∠PCD
=
x°,PM=PN
∵BP平分∠
ABC
∴∠ABP=∠PBC,PF=PN
∴PM=PF
∵∠BPC=40°
∴∠ABP=∠PBC=∠PCD?∠BPC=(x?40)°
∴∠CAB=∠ACD?∠ABC=2x°?2(x?40)°=80°
∵PM=PF,AP=AP,PF⊥BA,PM⊥AC
∴Rt△PAF
≌
Rt
△PAM
∴∠CAP=∠PAF=(180°?∠CAB)=
(180°?80°)=50°
故本题答案应为:∠CAB=80°,∠CAP=50°
21.证明:过D作DM⊥AB于M,DN⊥AC于N,
即∠EMD=∠FND=90°,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN(角平分线性质),
∵∠EAF+∠EDF=180°,
∴∠MED+∠AFD=360°-180°=180°,
∵∠AFD+∠NFD=180°,
∴∠MED=∠NFD,
在△EMD和△FND中
,
∴△EMD≌△FND(AAS),
∴DE=DF.
22.(1)证明:连接BD,CD,
∵
AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,解得:x=1,
∴BE=1,即AE=AB﹣BE=5﹣1=4.
23.解:如图所示,射线、为平角的三等分线;
如图所示,射线、为的三等分线.
