一元二次方程

(共19张PPT)
1、你还记得什么叫方程？什么叫方程的解吗？
2、什么是一元一次方程？它的一般形式是怎样的？
3、我们知道了利用一元一次方程可以解决生活中的一些实际问题，你还记得利用一元一次方程解决实际问题的步骤吗
(第一课时)
大江东去浪淘尽，千古风流数人物；
而立之年督东吴，早逝英年两位数；
十位恰小个位三，个位平方与寿符；
哪位学子算得快，多少年华属周瑜？
自学指导
1、阅读：P30————P32
2、思考：
（1）什么是一元二次方程及一般形式;
（2）会将一元二次方程化为一般形式;
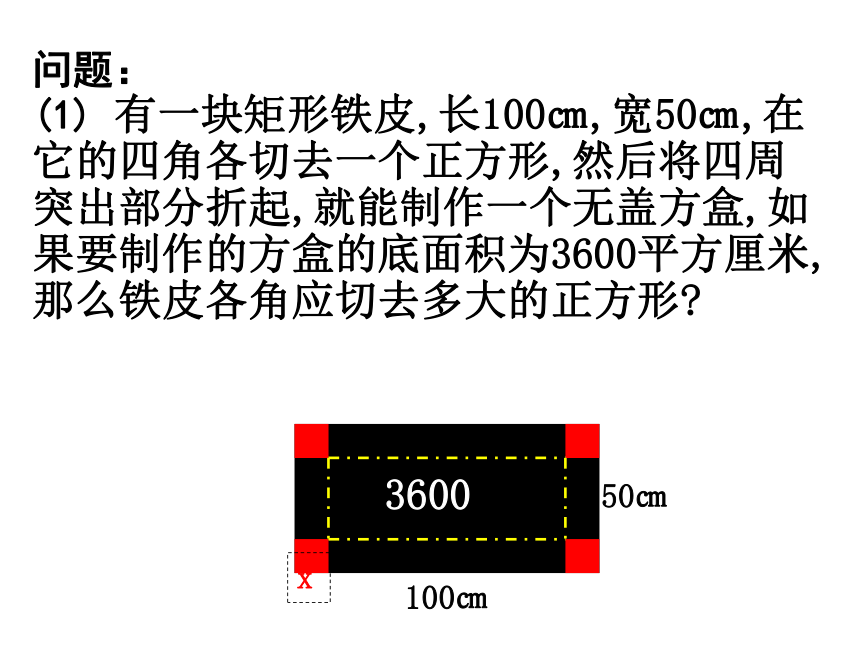
问题：
(1) 有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600平方厘米,那么铁皮各角应切去多大的正方形
100㎝
50㎝
x
3600
问题：
(2) 要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
（3）一个正方形的面积的2倍等于15，这个正方形的边长是多少？
（4）一个数比另一个数大3，且两个数之积为0，求这两个数。
这几个方程与一元一次方程的区别在哪里？它们有什么共同特点呢？
类比一元一次方程的定义,能否给出一元二次方程的概念呢
一元二次方程的概念
整式方程中只含有一个未知数(一元)，
并且未知数的最高次数是2(二次)，这样的方程叫做一元二次方程
一元二次方程的一般形式
一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把这种形式
(a,b,c为常数，a≠0）称为一元二次方程的一般形式。
为什么要限制a≠0，b,c可以为零吗？
想一想
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
做一做:判断下列方程是否为一元二次方程.
(1)X2+X=36
(2)X3+X2=36
(3)X2+3Y=36
(5)X2=X(X+1)+36
(6)ax2+bx+c=0
(a≠0)　
试试看：若关于x的方程(m-1)x2+3x-4=0是一元二
次方程, 则m的取值范围是______.
大胆探索
例1:
将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.
3x2-8x-10=0
该注意点什么？
合作探究
例题讲解
[例2] 将下列方程化为一般形式，并分别指出它们的二次项、一次项和常数项及它们的系数：
1.
2.
3.
二次项、二次项系数、一次项、一次项系数、常数项都是包括符号的
方
程 一般
形式 二次项
系数 一次项
系数 常数项
2x2-x=4
2y-4y2=0
(2x)2=(x+1)2
巩固提高
-4
2x2-x-4=0
2
-1
-4y2+2y=0
-4
2
0
3x2-2x-1=0
3
-2
-1
1.下列是一元二次方程的是（ ）
A. X2+3x-2 B. x2+3x-2=x2
C. X2=2+3x D. x2-x3+4=0
4.若关于x的方程kx2+x=2x2+1是一元二次方程，则
k的取值范围是_____.
2.写出一个一元二次方程，使它的各项系数之和为 6，
则方程可以是______.
3.关于x的一元二次方程(m-3)x2-(m-1)x-m=0的二次项
系数是_____,一次项系数是_____,常数项是_____.
做一做,看看你学会了吗
根据下列问题，列出关于x的方程，并将其化成一般形式。
1. 4个完全相同的正方形的面积之和为25，
求正方形的边长x。
2.一个直角三角形的斜边长为10，两条直角边
相差2，求较长的直角边长x。
3.参加一次聚会的每两个人都握了一次手，所
有人共握10次，求参加聚会的人数x.
学以致用
关于x的方程(m2-9)x2+(m+3)x+5m-1=0，
(1)当m取何值时是一元二次方程？
(2)当m取何值时是一元一次方程？
开动脑筋
[例３]方程（2a—4）x2 —2bx+a=0, 在什么条件下此方程为一元二次方程？在什么条件下此方程为一元一次方程？
解：当a≠2时是一元二次方程；
当a＝2，b≠0时是一元一次方程；
关于X的方程(2m2+3)x2+5x=13
一定是一元二次方程吗？为什么