11.2三角形全等的判定(含全章所有的判定)
文档属性
| 名称 | 11.2三角形全等的判定(含全章所有的判定) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-06 22:15:47 | ||
图片预览




文档简介
(共80张PPT)
三角形全等的探索
C
B
A
多边形全等的识别
若对应边相等,对应角相等
则两多边形全等
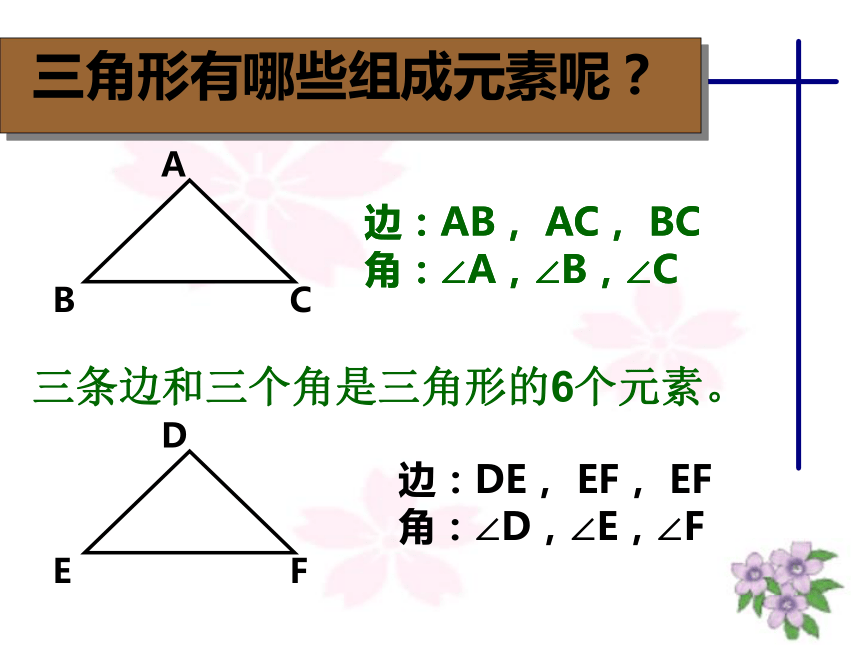
三角形有哪些组成元素呢?
三条边和三个角是三角形的6个元素。
C
B
A
边:AB, AC, BC
角:∠A,∠B,∠C
F
E
D
边:AB, AC, BC
角:∠A,∠B,∠C
边:DE, EF, EF
角:∠D,∠E,∠F
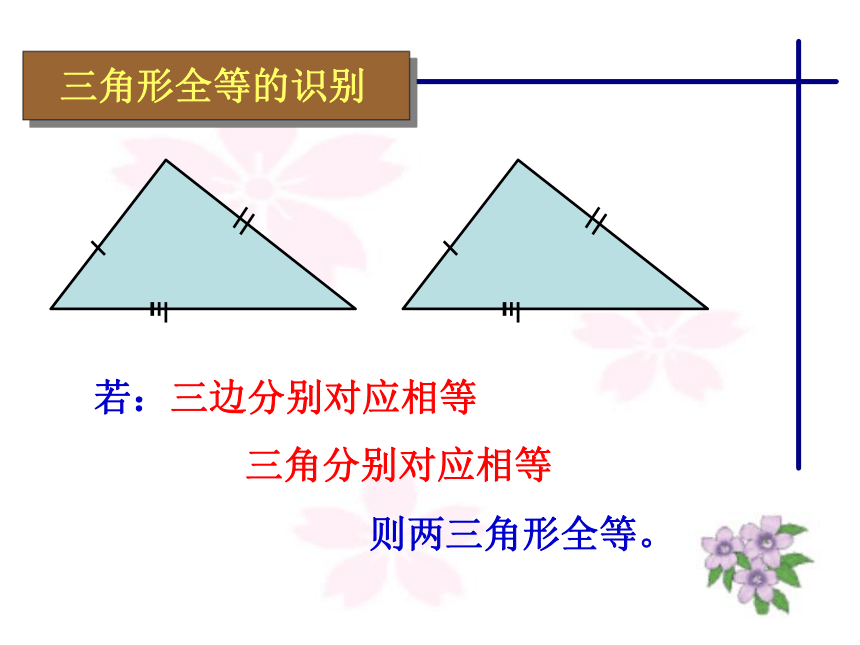
三角形全等的识别
若:三边分别对应相等
三角分别对应相等
则两三角形全等。
两个三角形至少要具备什么条件,即它们有多少组边或角分别对应相等时就全等呢?
三角形全等的探索
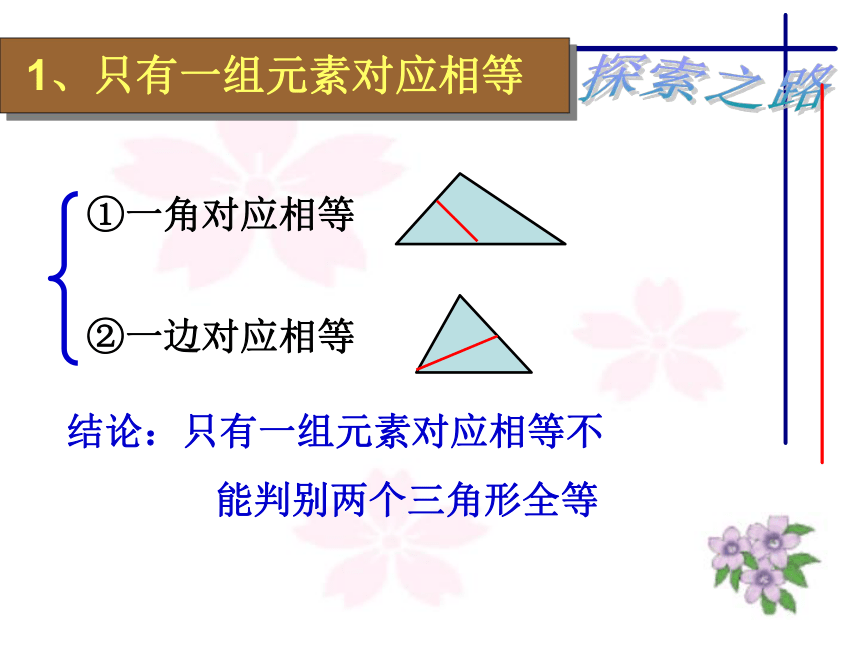
1、只有一组元素对应相等
①一角对应相等
②一边对应相等
探索之路
结论:只有一组元素对应相等不
能判别两个三角形全等
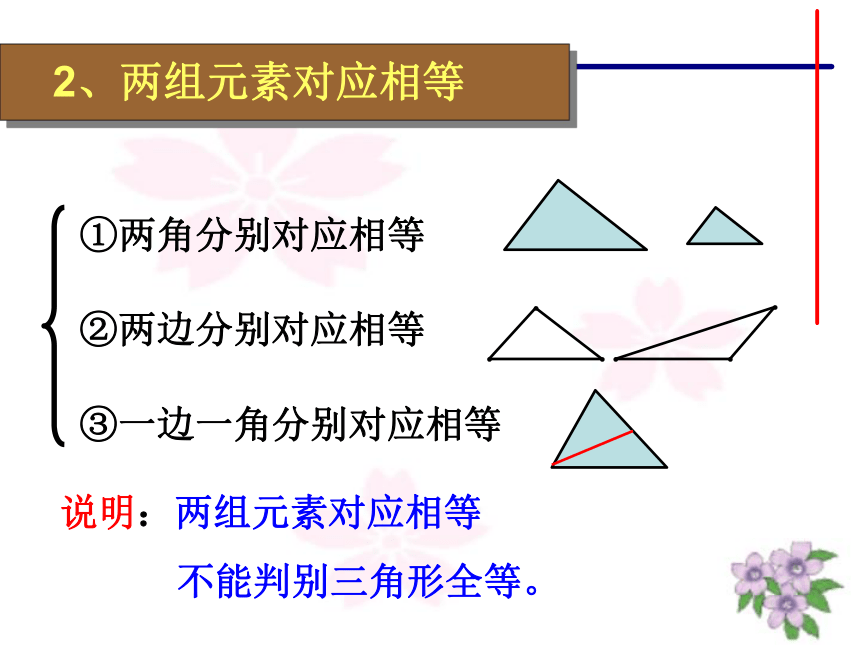
2、两组元素对应相等
②两边分别对应相等
①两角分别对应相等
③一边一角分别对应相等
说明:两组元素对应相等
不能判别三角形全等。
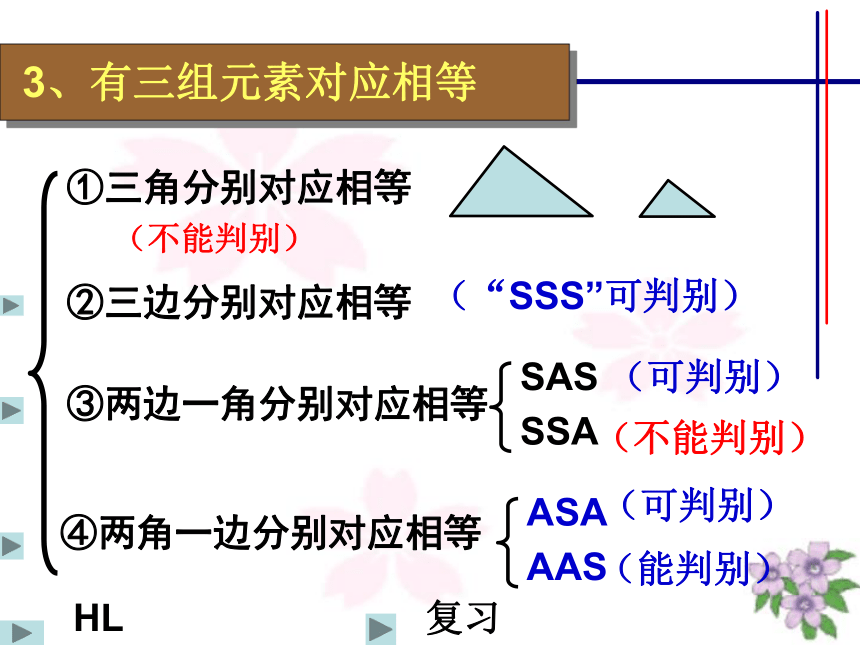
①三角分别对应相等
②三边分别对应相等
③两边一角分别对应相等
④两角一边分别对应相等
3、有三组元素对应相等
(不能判别)
(“SSS”可判别)
SAS
SSA
(可判别)
(不能判别)
ASA
AAS
(可判别)
(能判别)
复习
HL
探索与应用
“SSS”篇
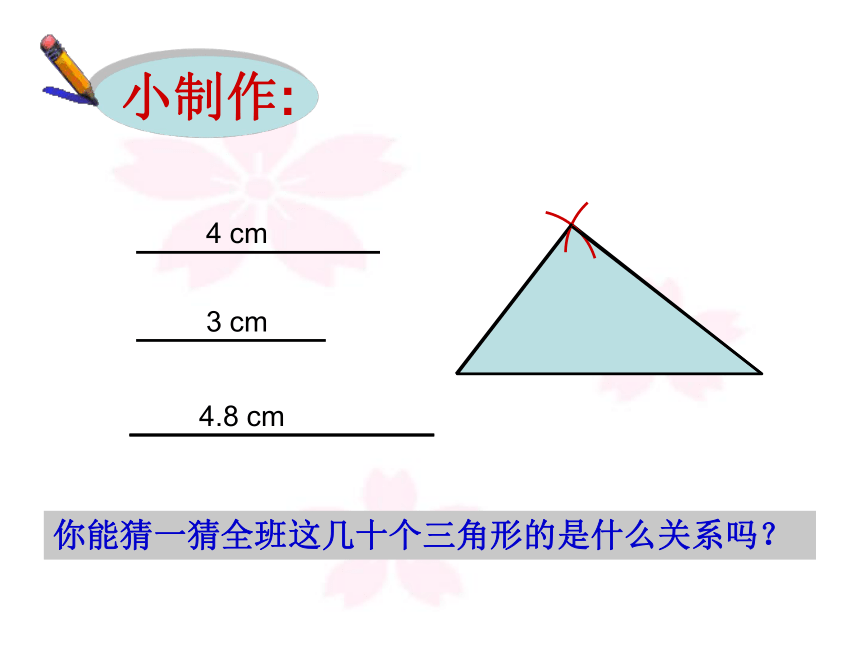
小制作:
4 cm
3 cm
4.8 cm
你能猜一猜全班这几十个三角形的是什么关系吗?
试一试
若另换三条能画成三角形的线段,我们画出的三角形还会全等吗?
这就是我们所熟悉的三角形的稳定性
概括:
如果两个三角形的三条边分别对应相等,那么这两个三角形全等
A
B
C
D
E
F
(简称: 边.边.边 或 S.S.S)
A
B
C
D
O
A
B
C
D
A
B
C
D
O
尝试 · 据条件判定下列的三角形是否全等
A
B
C
D
△ABC和△BAD
O
小试牛刀
如图,四边形ABCD中,AD=BC,AB=DC,试说明△ABC≌△CDA
A
B
C
D
注意:书写的条理性
如图,AB=AD,BC=DC,试说明∠B= ∠D
A
B
C
D
你也试一试:
如图,AB=EF,BC=DE,若AD=CF,则△ABC与△FED全等吗 说明理由.
继续探索
E
F
D
A
B
C
若△ABC向右平移一定距离,刚才的结论还成立吗
若边结BD,CE,则△BDA 与△ECF全等吗 为什么
还能找出一组三角形并说明它们全等吗?
数学、生活
有一块三角形的厚铁板,据需要,张师傅要把∠AOB平分开,但他身边只有一把直尺(可惜没有刻度)和一根细线,想一想,有什么好办法?说说你的方案。
A
O
B
A
O
B
·
C
·
D
·
M
A
O
B
·
C
·
D
·
M
探索与应用
“SAS”篇
两边及其夹角
两边及一边对角
(边角边)
(边边角)
三角形全等的探索
③两边一角分别对应相等
边角边
边边角
现有线段a=8cm,b=5cm,
(1)画 使AB=8cm,AC=5cm,
(2)画 使AB=8cm,BC=5cm,
实践出真知
请你归纳
如果两个三角形有两边及其夹角分别
对应相等,那么这两个三角形全等。
(简记为:SAS)
试一试:
B
A
D
C
O
根据”边角边“定理填写需要补充的条件,使结论成立;
解:在△AOB和△DOC中
∵ AO=DO,
= ,
BO=CO
∴ △AOB≌△D0C( )
∠AOB ∠DOC
≌
再试试
AB DC
生活中的数学
国庆期间,几名学生在钵池山公园,测量一池塘两端A,B的距离,设计了如下方案:如图,先在平地上取了一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测DE的长即为AB的距离,你认为这种方案可行吗 并加以说明.
A
B
C
E
D
例1
已知:如图,点A,B,C,D在同一条直线上,
AB=CD,∠D=∠ECA,EC=FD
请说明:AE=BF
AE和BF还有其它的关系吗 为什么
看谁反应快
如图,已知,AB=AC,AD=AE,∠BAE=∠CAD
试说明:∠B=∠C
练一练
例2
已知:如图,AB║DE,AB=DE,AF=DC,
请说明:△ECF≌△BFC
思维竞技场
≌
思考题
(2)连结BE,你还能得到什么结论 请写出来.(不要求说明理由)
探索与应用
“ASA与AAS”篇
探索之路
两角一边分别对应相等
(角边角)
(角角边)
两角一边
三角形全等的识别
已知两个角和一条线段,以这两个角为内角,以这条线段为两个角的夹边,画一个三角形.
做一做:
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.
归 纳
简记为 (A.S.A.)
符 号 语 言
≌
三角形全等的识别
根据题目条件,判别下面的两个三角形是否全等,并说明理由.
练一练
已知两个角和一条线段,以这两个角为内,以这条线段为一个角的对边,画一个三角形.
思 考:
A
B
C
D
E
F
如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.(A.A.S.)
A
B
C
D
E
F
符号语言:
①
②
③
例1:
例1:已知如图:
∠BDA=∠CEA,AE=AD
求证: △ABD≌△ACE.
注意:书写的条理性
如图:∠1=∠2,∠B=∠D,△ABC和△ADC全等吗?
你也试一试:
如图,∠ABC=∠DCB,试添加一个条件,使得△ABC≌△DCB,这个条件可以是
_________,或_______
你也试一试:
如图:△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由.
你也试一试:
若改为:AD、BE分别是两腰上的中线,△ABD和△BAE全等吗?试说明理由.
若改为:AD、BE分别是两腰上的高,△ABD和△BAE全等吗?试说明理由.
如图,AB//DC,AD//BC,BE⊥AC,DF ⊥ AC垂足为E、F。试说明:BE=DF
例2:探索继续
A
B
C
D
E
F
变形,如图(2)将上题中的条件“BE⊥AC,DF ⊥ AC”变为“BE //DF”,结论还成立吗?请说明你的理由。
A
B
C
D
E
F
探索与应用
“HL”
直角三形全等的识别
探索
直角三角形
全等的条件
两个三角形全等的条件
两边一角:SAS (夹角)
两角一边
ASA (夹边)
AAS (对边)
三边 SSS
判断
(1)两条直角边对应相等的两个直角三角形全等
(2)两个锐角对应相等的两个直角三角形全等
(3)一条直角边和一个锐角对应相等的两个直角三角形全等
(4)一条斜边和一个锐角对应相等的两个直角三角形全等
(5)两个直角三角形有一边一角对应相等则一定全等
(SAS)
(AAS 或 ASA)
(AAS 或 ASA)
因为直角三角形是一种特殊的三角形,所以一般三角形全等的条件都可以用来说明两个直角三角形全等
对于这种特殊的三角形而言,若只有两边相等,那么这两个直角三角形全等吗?
一般性:
特殊在那里?
让我们一起动动手吧!
(1)画∠PCQ=90°
(2)在射线CP上取CB=3cm
(3)以B为圆心,5cm为半径,画弧交射线CQ于点A。
(4)连接AB。
又多了一个朋友噢
斜边和一条直角边对应相等的两个直角三角形全等。
简写为“斜边、直角边”或“HL”
四边形ABCD中,CB=CD∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为( )
∟
C
D
A
B
如图:AC⊥BC,AD ⊥BD,垂足分别为C、D,AC=BD,△ABC与△BAD全等吗?
∟
∟
A
B
D
C
你来试一下如何?
∟
A
B
C
D
如图:AD⊥BC,AB=AC,你能找出其中的全等三角形吗?
你能知道AD和△ABC还有什么关系吗?
如图:AB=DF,CF=EB,AC⊥CE,DE ⊥CE,垂足分别为C、E。△ABC和△DFE全等吗?为什么?
∟
∟
A
B
C
D
E
F
如图:△ABC中,∠A=90°AB=AC=BE,E是BC上一点,DE⊥BC,如果BC=10cm,那么△DEC的周长是_______cm
A
B
E
C
D
如图:EB⊥AC,AB=EB,CE=DA,试说明AF⊥EC
E
A
B
C
D
F
能力升级
1、如图,△ABC中,∠ABC=45°,H是高AD与BE的交点,试说明:BH=AC。
探索与应用
复习篇
图形的全等
全等三角形
性质
判定
对
应
边
相
等
对
应
角
相
等
全等图形
能够完全重合
大小,形状相同
1、判断两个三角形全等的方法:
判定方法 条 件
边边边
(SSS)
三边对应相等
边角边
(SAS)
两边和他们的 对应相等
角边角
(ASA)
两角和他们的夹边对应相等
角角边
(AAS)
两角和 对应相等
夹角
其中一角的对边
2、判断两个直角三角形全等的方法:
A.一般三角形全等的判定方法对直角三角形全等的判定
同样适用.
B.
判定方法 条 件
直角边和斜边
(HL)
斜边和一条直角边对应相等
2、一般三角形全等判定方法的选择:
已知条件 可选择的判定方法
SAS
ASA
AAS
SAS
AAS
ASA
SSS
一边一角对应相等
两个角对应相等
两条边对应相等
练习:
判断题:
1.全等图形是指面积大小一样的图形
2.两个等边三角形一定是全等图形
3.周长相等的两个正方形面积也相等
4.全等三角形的对应高不一定相等
5、全等三角形的周长相等,面积相等
6、全等三角形对应边的中线相等。( )
7、面积相等的两个三角形全等。( )
8、两边和一角对应相等的两个三角形全 等。 ( )
√
√
×
×
练习:
1.如图,已知AC=DC,∠BCE=∠ACD,请添加一
个已知条件: ,使ΔABC≌ΔDEC.
2.如图,已知AB=AC,EB=EC,AE的延长线交BC于
点D,那么图中的全等三角形共有 对.
第3题
第4题
BC=EC
或∠B=∠DCE
或∠A=∠D
3
E
D
A
B
C
C
A
D
B
E
3.已知,在ΔABC和ΔDEF中,∠A=40 ,∠B=60 ,
∠D=80 ,∠E=60 ,你可再添加一个什么条
件使得ΔABC≌ΔFDE,并说明理由.
40
60
80
60
4.如图,已知,∠B=∠C,D,E,F分别在AB,BC,AC
上,且BD=CE,∠DEF=∠B,图中与ΔBDE全等
的三角形是 .请你写出理由.
ΔCEF
三角形全等的识别
已知:AB BC,DC BC,
DE AC,B,C,M为垂足,
AB=EC,试说明AC=DE
4、已知,如图,AB=AC,BD=DC,则
AD与BC有什么样的位置关系 WHY?
A
B
C
D
A
D
E
B
C
若AB=AD,BE=DE,试说明BC=DC
三角形全等的识别
若AB、CD相交于点O,AB=CD,AD=CB,试说明∠A=∠C
O
C
B
D
A
三角形全等的识别
已知:如图,AB=AC, BAC= DAE, ABD = ACE
试说明AD=AE
练一练
A
B
C
D
E
如图:△ABC中,∠A=90°AB=AC=BE,E是BC上一点,DE⊥BC,如果BC=10cm,那么△DEC的周长是_______cm
A
B
E
C
D
勇攀高峰
如图所示,已知M是正方形ABCD的边AB的中点,MN⊥MD交∠CBE的平分线BN于点N,求证:MD=MN
若M是正方形ABCD的边AB的任一点,其余条件不变,上述结论还成立吗?
勇攀高峰
如图①所示,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B点和C点在AE的异侧,BD⊥AE于D点, CE⊥AE于E点;
如图③求证:若直线AE绕点A旋转到图③所示位置时(BD>CE),其余条件不变,问BD与DE、CE关系如何?直接写出结论,不必证明。
④归纳前面三题,用语言表达BD与DE、CE的关系。
如图②求证:若直线AE绕A旋转到图②所示位置时(BD图①
图②
图③
忠心祝福我们每个同学都可以给这一章画上一个完美的号!
三角形全等的探索
C
B
A
多边形全等的识别
若对应边相等,对应角相等
则两多边形全等
三角形有哪些组成元素呢?
三条边和三个角是三角形的6个元素。
C
B
A
边:AB, AC, BC
角:∠A,∠B,∠C
F
E
D
边:AB, AC, BC
角:∠A,∠B,∠C
边:DE, EF, EF
角:∠D,∠E,∠F
三角形全等的识别
若:三边分别对应相等
三角分别对应相等
则两三角形全等。
两个三角形至少要具备什么条件,即它们有多少组边或角分别对应相等时就全等呢?
三角形全等的探索
1、只有一组元素对应相等
①一角对应相等
②一边对应相等
探索之路
结论:只有一组元素对应相等不
能判别两个三角形全等
2、两组元素对应相等
②两边分别对应相等
①两角分别对应相等
③一边一角分别对应相等
说明:两组元素对应相等
不能判别三角形全等。
①三角分别对应相等
②三边分别对应相等
③两边一角分别对应相等
④两角一边分别对应相等
3、有三组元素对应相等
(不能判别)
(“SSS”可判别)
SAS
SSA
(可判别)
(不能判别)
ASA
AAS
(可判别)
(能判别)
复习
HL
探索与应用
“SSS”篇
小制作:
4 cm
3 cm
4.8 cm
你能猜一猜全班这几十个三角形的是什么关系吗?
试一试
若另换三条能画成三角形的线段,我们画出的三角形还会全等吗?
这就是我们所熟悉的三角形的稳定性
概括:
如果两个三角形的三条边分别对应相等,那么这两个三角形全等
A
B
C
D
E
F
(简称: 边.边.边 或 S.S.S)
A
B
C
D
O
A
B
C
D
A
B
C
D
O
尝试 · 据条件判定下列的三角形是否全等
A
B
C
D
△ABC和△BAD
O
小试牛刀
如图,四边形ABCD中,AD=BC,AB=DC,试说明△ABC≌△CDA
A
B
C
D
注意:书写的条理性
如图,AB=AD,BC=DC,试说明∠B= ∠D
A
B
C
D
你也试一试:
如图,AB=EF,BC=DE,若AD=CF,则△ABC与△FED全等吗 说明理由.
继续探索
E
F
D
A
B
C
若△ABC向右平移一定距离,刚才的结论还成立吗
若边结BD,CE,则△BDA 与△ECF全等吗 为什么
还能找出一组三角形并说明它们全等吗?
数学、生活
有一块三角形的厚铁板,据需要,张师傅要把∠AOB平分开,但他身边只有一把直尺(可惜没有刻度)和一根细线,想一想,有什么好办法?说说你的方案。
A
O
B
A
O
B
·
C
·
D
·
M
A
O
B
·
C
·
D
·
M
探索与应用
“SAS”篇
两边及其夹角
两边及一边对角
(边角边)
(边边角)
三角形全等的探索
③两边一角分别对应相等
边角边
边边角
现有线段a=8cm,b=5cm,
(1)画 使AB=8cm,AC=5cm,
(2)画 使AB=8cm,BC=5cm,
实践出真知
请你归纳
如果两个三角形有两边及其夹角分别
对应相等,那么这两个三角形全等。
(简记为:SAS)
试一试:
B
A
D
C
O
根据”边角边“定理填写需要补充的条件,使结论成立;
解:在△AOB和△DOC中
∵ AO=DO,
= ,
BO=CO
∴ △AOB≌△D0C( )
∠AOB ∠DOC
≌
再试试
AB DC
生活中的数学
国庆期间,几名学生在钵池山公园,测量一池塘两端A,B的距离,设计了如下方案:如图,先在平地上取了一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测DE的长即为AB的距离,你认为这种方案可行吗 并加以说明.
A
B
C
E
D
例1
已知:如图,点A,B,C,D在同一条直线上,
AB=CD,∠D=∠ECA,EC=FD
请说明:AE=BF
AE和BF还有其它的关系吗 为什么
看谁反应快
如图,已知,AB=AC,AD=AE,∠BAE=∠CAD
试说明:∠B=∠C
练一练
例2
已知:如图,AB║DE,AB=DE,AF=DC,
请说明:△ECF≌△BFC
思维竞技场
≌
思考题
(2)连结BE,你还能得到什么结论 请写出来.(不要求说明理由)
探索与应用
“ASA与AAS”篇
探索之路
两角一边分别对应相等
(角边角)
(角角边)
两角一边
三角形全等的识别
已知两个角和一条线段,以这两个角为内角,以这条线段为两个角的夹边,画一个三角形.
做一做:
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.
归 纳
简记为 (A.S.A.)
符 号 语 言
≌
三角形全等的识别
根据题目条件,判别下面的两个三角形是否全等,并说明理由.
练一练
已知两个角和一条线段,以这两个角为内,以这条线段为一个角的对边,画一个三角形.
思 考:
A
B
C
D
E
F
如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.(A.A.S.)
A
B
C
D
E
F
符号语言:
①
②
③
例1:
例1:已知如图:
∠BDA=∠CEA,AE=AD
求证: △ABD≌△ACE.
注意:书写的条理性
如图:∠1=∠2,∠B=∠D,△ABC和△ADC全等吗?
你也试一试:
如图,∠ABC=∠DCB,试添加一个条件,使得△ABC≌△DCB,这个条件可以是
_________,或_______
你也试一试:
如图:△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由.
你也试一试:
若改为:AD、BE分别是两腰上的中线,△ABD和△BAE全等吗?试说明理由.
若改为:AD、BE分别是两腰上的高,△ABD和△BAE全等吗?试说明理由.
如图,AB//DC,AD//BC,BE⊥AC,DF ⊥ AC垂足为E、F。试说明:BE=DF
例2:探索继续
A
B
C
D
E
F
变形,如图(2)将上题中的条件“BE⊥AC,DF ⊥ AC”变为“BE //DF”,结论还成立吗?请说明你的理由。
A
B
C
D
E
F
探索与应用
“HL”
直角三形全等的识别
探索
直角三角形
全等的条件
两个三角形全等的条件
两边一角:SAS (夹角)
两角一边
ASA (夹边)
AAS (对边)
三边 SSS
判断
(1)两条直角边对应相等的两个直角三角形全等
(2)两个锐角对应相等的两个直角三角形全等
(3)一条直角边和一个锐角对应相等的两个直角三角形全等
(4)一条斜边和一个锐角对应相等的两个直角三角形全等
(5)两个直角三角形有一边一角对应相等则一定全等
(SAS)
(AAS 或 ASA)
(AAS 或 ASA)
因为直角三角形是一种特殊的三角形,所以一般三角形全等的条件都可以用来说明两个直角三角形全等
对于这种特殊的三角形而言,若只有两边相等,那么这两个直角三角形全等吗?
一般性:
特殊在那里?
让我们一起动动手吧!
(1)画∠PCQ=90°
(2)在射线CP上取CB=3cm
(3)以B为圆心,5cm为半径,画弧交射线CQ于点A。
(4)连接AB。
又多了一个朋友噢
斜边和一条直角边对应相等的两个直角三角形全等。
简写为“斜边、直角边”或“HL”
四边形ABCD中,CB=CD∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为( )
∟
C
D
A
B
如图:AC⊥BC,AD ⊥BD,垂足分别为C、D,AC=BD,△ABC与△BAD全等吗?
∟
∟
A
B
D
C
你来试一下如何?
∟
A
B
C
D
如图:AD⊥BC,AB=AC,你能找出其中的全等三角形吗?
你能知道AD和△ABC还有什么关系吗?
如图:AB=DF,CF=EB,AC⊥CE,DE ⊥CE,垂足分别为C、E。△ABC和△DFE全等吗?为什么?
∟
∟
A
B
C
D
E
F
如图:△ABC中,∠A=90°AB=AC=BE,E是BC上一点,DE⊥BC,如果BC=10cm,那么△DEC的周长是_______cm
A
B
E
C
D
如图:EB⊥AC,AB=EB,CE=DA,试说明AF⊥EC
E
A
B
C
D
F
能力升级
1、如图,△ABC中,∠ABC=45°,H是高AD与BE的交点,试说明:BH=AC。
探索与应用
复习篇
图形的全等
全等三角形
性质
判定
对
应
边
相
等
对
应
角
相
等
全等图形
能够完全重合
大小,形状相同
1、判断两个三角形全等的方法:
判定方法 条 件
边边边
(SSS)
三边对应相等
边角边
(SAS)
两边和他们的 对应相等
角边角
(ASA)
两角和他们的夹边对应相等
角角边
(AAS)
两角和 对应相等
夹角
其中一角的对边
2、判断两个直角三角形全等的方法:
A.一般三角形全等的判定方法对直角三角形全等的判定
同样适用.
B.
判定方法 条 件
直角边和斜边
(HL)
斜边和一条直角边对应相等
2、一般三角形全等判定方法的选择:
已知条件 可选择的判定方法
SAS
ASA
AAS
SAS
AAS
ASA
SSS
一边一角对应相等
两个角对应相等
两条边对应相等
练习:
判断题:
1.全等图形是指面积大小一样的图形
2.两个等边三角形一定是全等图形
3.周长相等的两个正方形面积也相等
4.全等三角形的对应高不一定相等
5、全等三角形的周长相等,面积相等
6、全等三角形对应边的中线相等。( )
7、面积相等的两个三角形全等。( )
8、两边和一角对应相等的两个三角形全 等。 ( )
√
√
×
×
练习:
1.如图,已知AC=DC,∠BCE=∠ACD,请添加一
个已知条件: ,使ΔABC≌ΔDEC.
2.如图,已知AB=AC,EB=EC,AE的延长线交BC于
点D,那么图中的全等三角形共有 对.
第3题
第4题
BC=EC
或∠B=∠DCE
或∠A=∠D
3
E
D
A
B
C
C
A
D
B
E
3.已知,在ΔABC和ΔDEF中,∠A=40 ,∠B=60 ,
∠D=80 ,∠E=60 ,你可再添加一个什么条
件使得ΔABC≌ΔFDE,并说明理由.
40
60
80
60
4.如图,已知,∠B=∠C,D,E,F分别在AB,BC,AC
上,且BD=CE,∠DEF=∠B,图中与ΔBDE全等
的三角形是 .请你写出理由.
ΔCEF
三角形全等的识别
已知:AB BC,DC BC,
DE AC,B,C,M为垂足,
AB=EC,试说明AC=DE
4、已知,如图,AB=AC,BD=DC,则
AD与BC有什么样的位置关系 WHY?
A
B
C
D
A
D
E
B
C
若AB=AD,BE=DE,试说明BC=DC
三角形全等的识别
若AB、CD相交于点O,AB=CD,AD=CB,试说明∠A=∠C
O
C
B
D
A
三角形全等的识别
已知:如图,AB=AC, BAC= DAE, ABD = ACE
试说明AD=AE
练一练
A
B
C
D
E
如图:△ABC中,∠A=90°AB=AC=BE,E是BC上一点,DE⊥BC,如果BC=10cm,那么△DEC的周长是_______cm
A
B
E
C
D
勇攀高峰
如图所示,已知M是正方形ABCD的边AB的中点,MN⊥MD交∠CBE的平分线BN于点N,求证:MD=MN
若M是正方形ABCD的边AB的任一点,其余条件不变,上述结论还成立吗?
勇攀高峰
如图①所示,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B点和C点在AE的异侧,BD⊥AE于D点, CE⊥AE于E点;
如图③求证:若直线AE绕点A旋转到图③所示位置时(BD>CE),其余条件不变,问BD与DE、CE关系如何?直接写出结论,不必证明。
④归纳前面三题,用语言表达BD与DE、CE的关系。
如图②求证:若直线AE绕A旋转到图②所示位置时(BD
图②
图③
忠心祝福我们每个同学都可以给这一章画上一个完美的号!
