北师大版九年级数学上册单元冲刺卷附答案:第三章 概率的进一步认识(Word版)
文档属性
| 名称 | 北师大版九年级数学上册单元冲刺卷附答案:第三章 概率的进一步认识(Word版) |  | |
| 格式 | zip | ||
| 文件大小 | 692.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 11:11:55 | ||
图片预览



文档简介
[模拟]第三章
概率的进一步认识
一、选择题(共15小题;共45分)
1.
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有
个,这些球除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率分别稳定在
和
,则布袋中白色球的个数可能是
A.
B.
C.
D.
2.
将一个正六面体骰子连掷
次,它们的点数都是
的概率是
A.
B.
C.
D.
3.
在一个不透明的袋子中装有
个除颜色外完全相同的小球,其中白球
个,黄球
个,红球
个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是
A.
B.
C.
D.
4.
学校新开设了航模、彩绘、泥塑三个社团,如果征征、舟舟两名同学每人随机选择参加其中一个社团,那么征征和舟舟选到同一社团的概率是
A.
B.
C.
D.
5.
在一个不透明的纸箱中放入
个除颜色外其他都完全相同的球,这些球中有
个红球,每次将球摇匀后任意摸出一个球,记下颜色再放回纸箱中,通过大量的重复摸球实验后发现摸到红球的频率稳定在
,因此可以估算出
的值大约是
A.
B.
C.
D.
6.
袋子里有
个球,标有
,,,,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于
的概率是
A.
B.
C.
D.
7.
晓辉为练习射击,共射击
次,其中
次击中靶子,由此可以估计,晓辉射击一次击中靶子的概率约是
A.
B.
C.
D.
8.
一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来的情况下,为估计白球的个数,小刚向盒中放了
个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断重复,共摸球
次,其中
次摸到黑球,估计盒中大约有白球
A.
个
B.
个
C.
个
D.
个
9.
有一箱子装有
张分别标示
、
、
的号码牌,已知小南以每次取一张且取后不放回的方式,先后取出
张牌,组成一个两位数,取出第
张牌的号码为十位数,第
张牌的号码为个位数,则组成的二位数为
的倍数的概率为
A.
B.
C.
D.
10.
掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有
至
六个数.连续掷两次,掷得面向上的点数之和是
的倍数的概率为
A.
B.
C.
D.
11.
在一个不透明的口袋里,装有仅颜色不同的黑球、白球若干只.某小组做摸球实验:将球搅匀后从中随机摸出一个,记下颜色,再放回袋中,不断重复.下表是活动中的一组数据,则摸到白球的概率约是
A.
B.
C.
D.
12.
小明与小亮两家准备从甲、乙、丙三个景点中选择一处游玩,小明与小亮通过抽签的方式确定景点,则两家抽到同一景点的概率是
A.
B.
C.
D.
13.
布袋中有除颜色外完全相同的
个红球,
个黄球,
个白球,从布袋中同时随机摸出两个球都是红球的概率为
A.
B.
C.
D.
14.
如图所示的两个圆盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是
A.
B.
C.
D.
15.
掷两枚普通正六面体骰子,所得点数之和为
的概率为
A.
B.
C.
D.
二、填空题(共8小题;共40分)
16.
从甲、乙、丙、丁
名三好学生中随机抽取
名学生担任校国旗队升旗手,则抽取的
名学生恰好是乙和丙的概率是
?.
17.
一个不透明的盒子里有
个除颜色外其他完全相同的小球,其中有
个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子.通过大量重复摸球试验后发现,找到黄球的频率稳定在
,那么可以推算出
大约是
?.
18.
“六?一”期间,小洁的妈妈经营的玩具店进了一纸箱除颜色外都相同的散装塑料球共
个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下其颜色,把它放回纸箱中;搅匀后再随机摸出一个球记下其颜色,把它放回纸箱中;.多次重复上述过程后,发现摸到红球的频率逐渐稳定在
,由此可以估计纸箱内红球的个数约是
?个.
19.
为了估计暗箱里白球的数量(箱内只有白球),将
个红球放进去,随机摸出一个球,记下颜色后放回,搅匀后再摸出一个球记下颜色,多次重复或发现红球出现的频率约为
,那么可以估计暗箱里白球的数量大约为
?
个.
20.
在一只不透明的口袋中放人红球
个,黑球
个,黄球
个,这些球除色不同外其他完全相同.搅匀后随机从中摸出一个,恰好是黄球的概率为
,则放人口袋中的黄球总数
?.
21.
点
的坐标是
,从
,,,,
这五个数中任取一个数作为
的值,再从余下的四个数中任取一个数作为
的值,则点
在平面直角坐标系中第二象限内的概率是
?.
22.
在背面完全相同,正面上分别标有两个连续奇数
,(其中
)的卡片
张.小明将其混合后,正面朝上放置在桌面上,并从中随机地抽取一张,则该卡片上两个数的各位数之和(例如:若取到标有
,
的卡片,则卡片上两个数的各位数之和为
)小于
的概率为
?.
23.
国务院办公厅在
年
月
日发布了《中国足球发展改革总体方案
》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛活动,在本次知识竞赛活动中,A,B,C,D
四所学校表现突出,现决定把这四所学校随机分成两组,每组两所学校举行一场足球友谊赛,则
A
与
B两所学校能分在同一组的概率为
?.
三、解答题(共5小题;共65分)
24.
六()班举行联欢活动,同学们把写有
号到
号学号的小纸条放入一个箱中,从中任意抽取一张纸条,求:
(1)抽到学号是
号的可能性的大小;
(2)抽到能被
整除的学号的可能性的大小.
25.
一个口袋中有
个红球和若干个白球,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下其颜色,再把它放回口袋中.不断重复上述过程,实验中总共摸了
次,其中有
次摸到红球.
26.
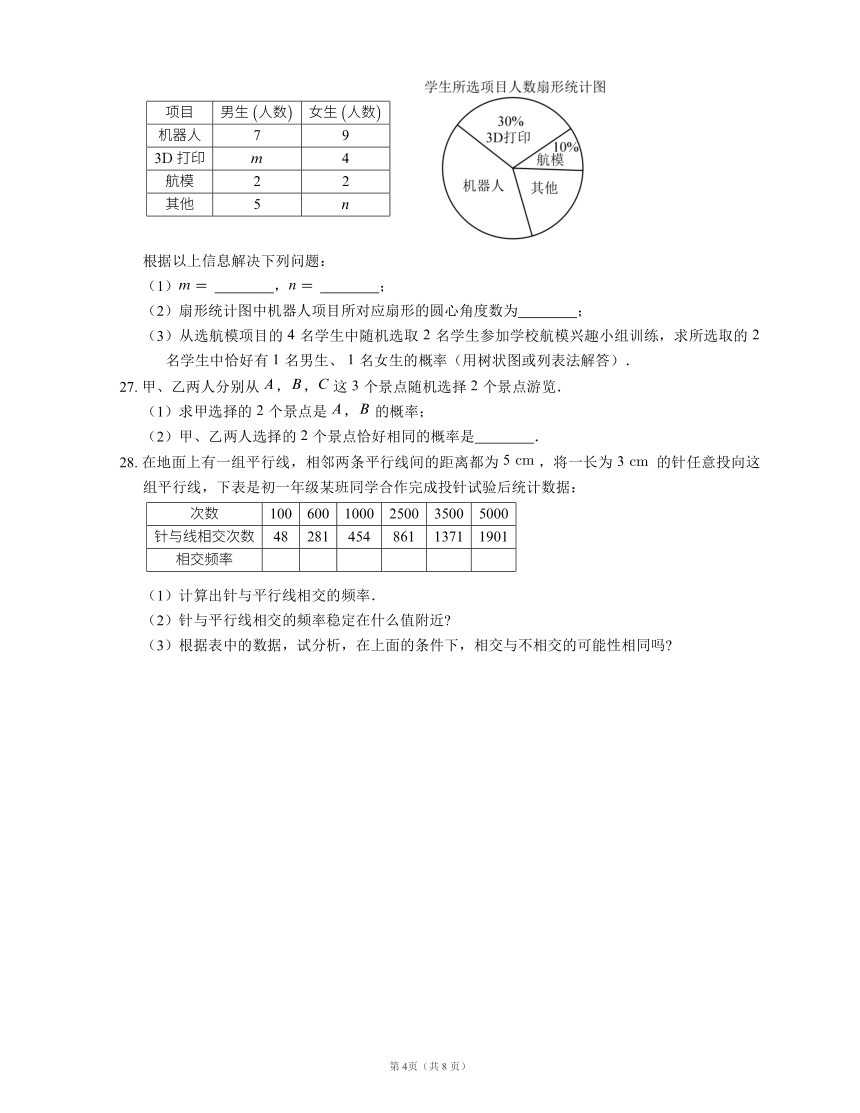
某班针对“你最喜爱的课外活动项目”对全班学生进行调査(每名学生分别选一个活动项目),并根据调查结果列出如下统计表,绘制成如下扇形统计图:
根据以上信息解决下列问题:
(1)
?,
?;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为
?;
(3)从选航模项目的
名学生中随机选取
名学生参加学校航模兴趣小组训练,求所选取的
名学生中恰好有
名男生、
名女生的概率(用树状图或列表法解答).
27.
甲、乙两人分别从
,,
这
个景点随机选择
个景点游览.
(1)求甲选择的
个景点是
,
的概率;
(2)甲、乙两人选择的
个景点恰好相同的概率是
?.
28.
在地面上有一组平行线,相邻两条平行线间的距离都为
,将一长为
的针任意投向这组平行线,下表是初一年级某班同学合作完成投针试验后统计数据:
(1)计算出针与平行线相交的频率.
(2)针与平行线相交的频率稳定在什么值附近?
(3)根据表中的数据,试分析,在上面的条件下,相交与不相交的可能性相同吗?
答案
第一部分
1.
C
2.
D
3.
C
【解析】一共有
种情况,其中两次都是红球的情况有
种,所以概率为
.
4.
C
【解析】本题考查列表法求概率.将征征、舟舟两名同学参加社团的可能情况列表如下:
由上表可知征征和舟舟选择的可能情况有
种,其中征征和舟舟选到同一社团的可能情况有
种,所以概率为
.
5.
D
6.
C
【解析】画树状图得:
共有
种等可能的结果,抽取的两个球数字之和大于
的有
种情况,
抽取的两个球数字之和大于
的概率是:.
7.
C
8.
A
【解析】.
9.
C
【解析】画树状图为:
共有
种等可能的结果数,其中组成的二位数为
的倍数的结果数为
,
所以组成的二位数为
的倍数的概率
.
10.
C
11.
C
12.
A
13.
A
14.
C
【解析】列表得:
一共有
种情况,两个指针同时落在偶数上的有
种情况,
两个指针同时落在偶数上的概率是
.
15.
A
【解析】列表得:
共有
种等可能的结果,所得点数之和为
的有
种情况,
所得点数之和为
的概率为:.
第二部分
16.
17.
18.
【解析】设红球的个数为
.
红球的频率在
附近波动,
摸出红球的概率为
,即
,解得
.
所以可以估计红球的个数为
.
19.
【解析】设暗箱里白球的数量是
,则根据题意得:,解得:.
20.
21.
【解析】画树状图为:
共有
种等可能的结果数,其中点
在平面直角坐标系中第二象限内的结果数为
,
所以点
在平面直角坐标系中第二象限内的概率
.
22.
23.
第三部分
24.
(1)
纸条共有
张,学号是
号的只有
个,
.
??????(2)
被
整除的数有:,,,,,,,,
个数,
.
25.
设估计口袋中白球
个.
由题意
,解得
.
答:估计口袋中有
个白球.
26.
(1)
;
【解析】
本次调查的总人数为
(人),
,机器人对应的百分比为
,
则其他项目对应百分比为
,
.
??????(2)
【解析】扇形统计图中机器人项目所对应扇形的圆心角度数为
.
??????(3)
列表得:
由表格可知,共有
种可能出现的结果,并且它们都是等可能的,其中选取“
名男生、
名女生”有
种可能.
.
27.
(1)
甲从
,,
这
个景点中随机抽取
个景点,所有可能出现的结果共有
种,即
,,,
这些结果出现的可能性相等,所有的结果中,满足甲选择的
个景点是
,(记为事件
)的结果有
种,即
,
所以
.
??????(2)
28.
(1)
;;;;;
【解析】;
由表中的数据可知针与平行线相交的频率分别是:;;;;;.
??????(2)
针与平行线相交频率稳定值约为
.因为当试验次数较大时,试验频率趋于稳定.
??????(3)
由表中频率的变化,可以得出针与平行线相交与不相交的可能性不完全相同.
第1页(共1
页)
概率的进一步认识
一、选择题(共15小题;共45分)
1.
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有
个,这些球除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率分别稳定在
和
,则布袋中白色球的个数可能是
A.
B.
C.
D.
2.
将一个正六面体骰子连掷
次,它们的点数都是
的概率是
A.
B.
C.
D.
3.
在一个不透明的袋子中装有
个除颜色外完全相同的小球,其中白球
个,黄球
个,红球
个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是
A.
B.
C.
D.
4.
学校新开设了航模、彩绘、泥塑三个社团,如果征征、舟舟两名同学每人随机选择参加其中一个社团,那么征征和舟舟选到同一社团的概率是
A.
B.
C.
D.
5.
在一个不透明的纸箱中放入
个除颜色外其他都完全相同的球,这些球中有
个红球,每次将球摇匀后任意摸出一个球,记下颜色再放回纸箱中,通过大量的重复摸球实验后发现摸到红球的频率稳定在
,因此可以估算出
的值大约是
A.
B.
C.
D.
6.
袋子里有
个球,标有
,,,,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于
的概率是
A.
B.
C.
D.
7.
晓辉为练习射击,共射击
次,其中
次击中靶子,由此可以估计,晓辉射击一次击中靶子的概率约是
A.
B.
C.
D.
8.
一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来的情况下,为估计白球的个数,小刚向盒中放了
个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断重复,共摸球
次,其中
次摸到黑球,估计盒中大约有白球
A.
个
B.
个
C.
个
D.
个
9.
有一箱子装有
张分别标示
、
、
的号码牌,已知小南以每次取一张且取后不放回的方式,先后取出
张牌,组成一个两位数,取出第
张牌的号码为十位数,第
张牌的号码为个位数,则组成的二位数为
的倍数的概率为
A.
B.
C.
D.
10.
掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有
至
六个数.连续掷两次,掷得面向上的点数之和是
的倍数的概率为
A.
B.
C.
D.
11.
在一个不透明的口袋里,装有仅颜色不同的黑球、白球若干只.某小组做摸球实验:将球搅匀后从中随机摸出一个,记下颜色,再放回袋中,不断重复.下表是活动中的一组数据,则摸到白球的概率约是
A.
B.
C.
D.
12.
小明与小亮两家准备从甲、乙、丙三个景点中选择一处游玩,小明与小亮通过抽签的方式确定景点,则两家抽到同一景点的概率是
A.
B.
C.
D.
13.
布袋中有除颜色外完全相同的
个红球,
个黄球,
个白球,从布袋中同时随机摸出两个球都是红球的概率为
A.
B.
C.
D.
14.
如图所示的两个圆盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是
A.
B.
C.
D.
15.
掷两枚普通正六面体骰子,所得点数之和为
的概率为
A.
B.
C.
D.
二、填空题(共8小题;共40分)
16.
从甲、乙、丙、丁
名三好学生中随机抽取
名学生担任校国旗队升旗手,则抽取的
名学生恰好是乙和丙的概率是
?.
17.
一个不透明的盒子里有
个除颜色外其他完全相同的小球,其中有
个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子.通过大量重复摸球试验后发现,找到黄球的频率稳定在
,那么可以推算出
大约是
?.
18.
“六?一”期间,小洁的妈妈经营的玩具店进了一纸箱除颜色外都相同的散装塑料球共
个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下其颜色,把它放回纸箱中;搅匀后再随机摸出一个球记下其颜色,把它放回纸箱中;.多次重复上述过程后,发现摸到红球的频率逐渐稳定在
,由此可以估计纸箱内红球的个数约是
?个.
19.
为了估计暗箱里白球的数量(箱内只有白球),将
个红球放进去,随机摸出一个球,记下颜色后放回,搅匀后再摸出一个球记下颜色,多次重复或发现红球出现的频率约为
,那么可以估计暗箱里白球的数量大约为
?
个.
20.
在一只不透明的口袋中放人红球
个,黑球
个,黄球
个,这些球除色不同外其他完全相同.搅匀后随机从中摸出一个,恰好是黄球的概率为
,则放人口袋中的黄球总数
?.
21.
点
的坐标是
,从
,,,,
这五个数中任取一个数作为
的值,再从余下的四个数中任取一个数作为
的值,则点
在平面直角坐标系中第二象限内的概率是
?.
22.
在背面完全相同,正面上分别标有两个连续奇数
,(其中
)的卡片
张.小明将其混合后,正面朝上放置在桌面上,并从中随机地抽取一张,则该卡片上两个数的各位数之和(例如:若取到标有
,
的卡片,则卡片上两个数的各位数之和为
)小于
的概率为
?.
23.
国务院办公厅在
年
月
日发布了《中国足球发展改革总体方案
》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛活动,在本次知识竞赛活动中,A,B,C,D
四所学校表现突出,现决定把这四所学校随机分成两组,每组两所学校举行一场足球友谊赛,则
A
与
B两所学校能分在同一组的概率为
?.
三、解答题(共5小题;共65分)
24.
六()班举行联欢活动,同学们把写有
号到
号学号的小纸条放入一个箱中,从中任意抽取一张纸条,求:
(1)抽到学号是
号的可能性的大小;
(2)抽到能被
整除的学号的可能性的大小.
25.
一个口袋中有
个红球和若干个白球,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下其颜色,再把它放回口袋中.不断重复上述过程,实验中总共摸了
次,其中有
次摸到红球.
26.
某班针对“你最喜爱的课外活动项目”对全班学生进行调査(每名学生分别选一个活动项目),并根据调查结果列出如下统计表,绘制成如下扇形统计图:
根据以上信息解决下列问题:
(1)
?,
?;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为
?;
(3)从选航模项目的
名学生中随机选取
名学生参加学校航模兴趣小组训练,求所选取的
名学生中恰好有
名男生、
名女生的概率(用树状图或列表法解答).
27.
甲、乙两人分别从
,,
这
个景点随机选择
个景点游览.
(1)求甲选择的
个景点是
,
的概率;
(2)甲、乙两人选择的
个景点恰好相同的概率是
?.
28.
在地面上有一组平行线,相邻两条平行线间的距离都为
,将一长为
的针任意投向这组平行线,下表是初一年级某班同学合作完成投针试验后统计数据:
(1)计算出针与平行线相交的频率.
(2)针与平行线相交的频率稳定在什么值附近?
(3)根据表中的数据,试分析,在上面的条件下,相交与不相交的可能性相同吗?
答案
第一部分
1.
C
2.
D
3.
C
【解析】一共有
种情况,其中两次都是红球的情况有
种,所以概率为
.
4.
C
【解析】本题考查列表法求概率.将征征、舟舟两名同学参加社团的可能情况列表如下:
由上表可知征征和舟舟选择的可能情况有
种,其中征征和舟舟选到同一社团的可能情况有
种,所以概率为
.
5.
D
6.
C
【解析】画树状图得:
共有
种等可能的结果,抽取的两个球数字之和大于
的有
种情况,
抽取的两个球数字之和大于
的概率是:.
7.
C
8.
A
【解析】.
9.
C
【解析】画树状图为:
共有
种等可能的结果数,其中组成的二位数为
的倍数的结果数为
,
所以组成的二位数为
的倍数的概率
.
10.
C
11.
C
12.
A
13.
A
14.
C
【解析】列表得:
一共有
种情况,两个指针同时落在偶数上的有
种情况,
两个指针同时落在偶数上的概率是
.
15.
A
【解析】列表得:
共有
种等可能的结果,所得点数之和为
的有
种情况,
所得点数之和为
的概率为:.
第二部分
16.
17.
18.
【解析】设红球的个数为
.
红球的频率在
附近波动,
摸出红球的概率为
,即
,解得
.
所以可以估计红球的个数为
.
19.
【解析】设暗箱里白球的数量是
,则根据题意得:,解得:.
20.
21.
【解析】画树状图为:
共有
种等可能的结果数,其中点
在平面直角坐标系中第二象限内的结果数为
,
所以点
在平面直角坐标系中第二象限内的概率
.
22.
23.
第三部分
24.
(1)
纸条共有
张,学号是
号的只有
个,
.
??????(2)
被
整除的数有:,,,,,,,,
个数,
.
25.
设估计口袋中白球
个.
由题意
,解得
.
答:估计口袋中有
个白球.
26.
(1)
;
【解析】
本次调查的总人数为
(人),
,机器人对应的百分比为
,
则其他项目对应百分比为
,
.
??????(2)
【解析】扇形统计图中机器人项目所对应扇形的圆心角度数为
.
??????(3)
列表得:
由表格可知,共有
种可能出现的结果,并且它们都是等可能的,其中选取“
名男生、
名女生”有
种可能.
.
27.
(1)
甲从
,,
这
个景点中随机抽取
个景点,所有可能出现的结果共有
种,即
,,,
这些结果出现的可能性相等,所有的结果中,满足甲选择的
个景点是
,(记为事件
)的结果有
种,即
,
所以
.
??????(2)
28.
(1)
;;;;;
【解析】;
由表中的数据可知针与平行线相交的频率分别是:;;;;;.
??????(2)
针与平行线相交频率稳定值约为
.因为当试验次数较大时,试验频率趋于稳定.
??????(3)
由表中频率的变化,可以得出针与平行线相交与不相交的可能性不完全相同.
第1页(共1
页)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
