人教版八年级上册数学:11.3多边形其内角和培优同步习题(word版,含答案)
文档属性
| 名称 | 人教版八年级上册数学:11.3多边形其内角和培优同步习题(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 15:49:38 | ||
图片预览


文档简介
人教版八年级上册数学
11.3多边形习题
1.动手操作,探究:
探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
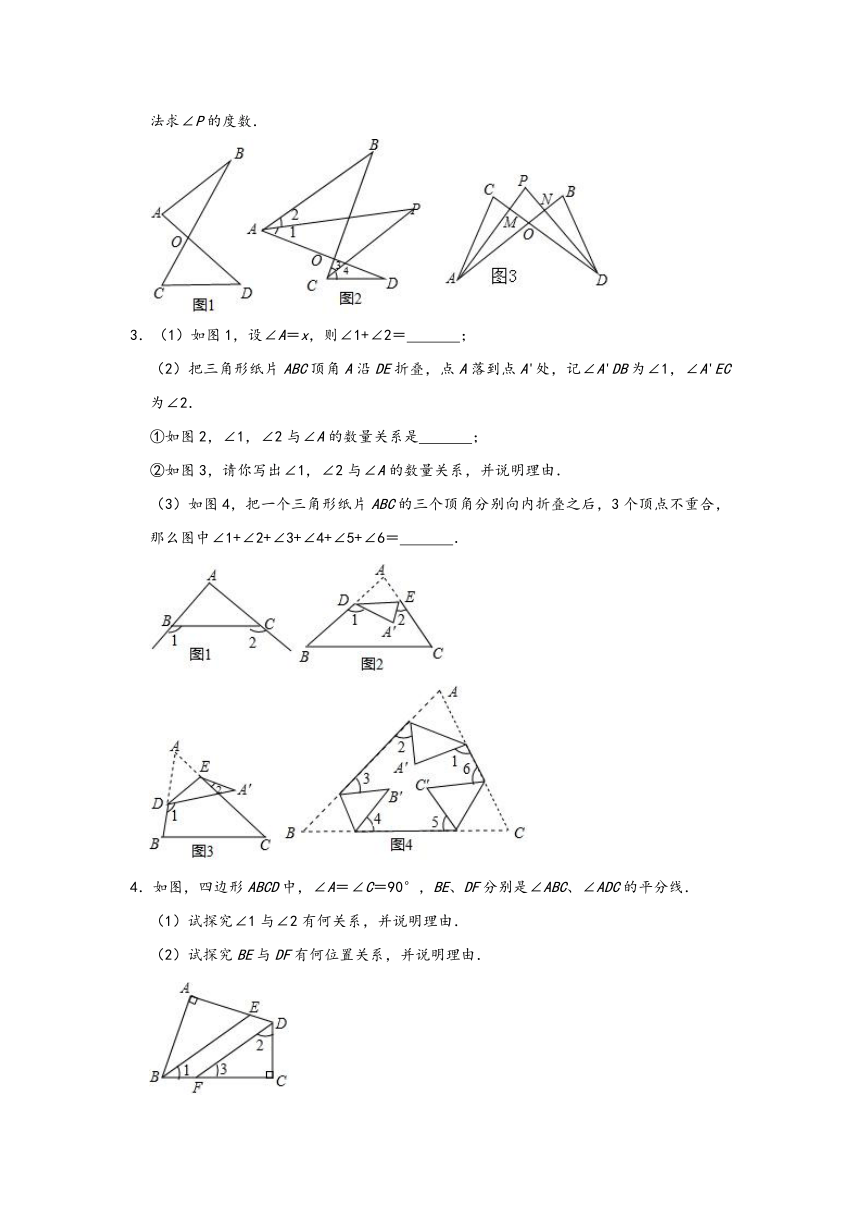
已知:如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究二:若将△ADC改为任意四边形ABCD呢?
已知:如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.(写出说理过程)
探究三:若将上题中的四边形ABCD改为六边形ABCDEF(图(3))呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:
.
2.【问题背景】小明在学习多边形时,把如图1的图形成为“8”字形,并得出如下结论:∠A+∠B=∠C+∠D,请你说明理由;
(2)【尝试应用】如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的
度数;
小明结合(1)中的结论并利用方程思想轻松解答如下:
解:由AP、CP分别平分∠BAD、∠BCD,可设∠1=∠2=x,∠3=∠4=y,
由(1)的结论得:,①+②,
得2∠P+x+y=x+y+∠B+∠D
∴(∠B+∠D)=26°
(3)【拓展延伸】如图3,已知∠C=α,∠B=β,∠CAP=∠CAB,∠CDP=∠CDB,请利用上述结论或方
法求∠P的度数.
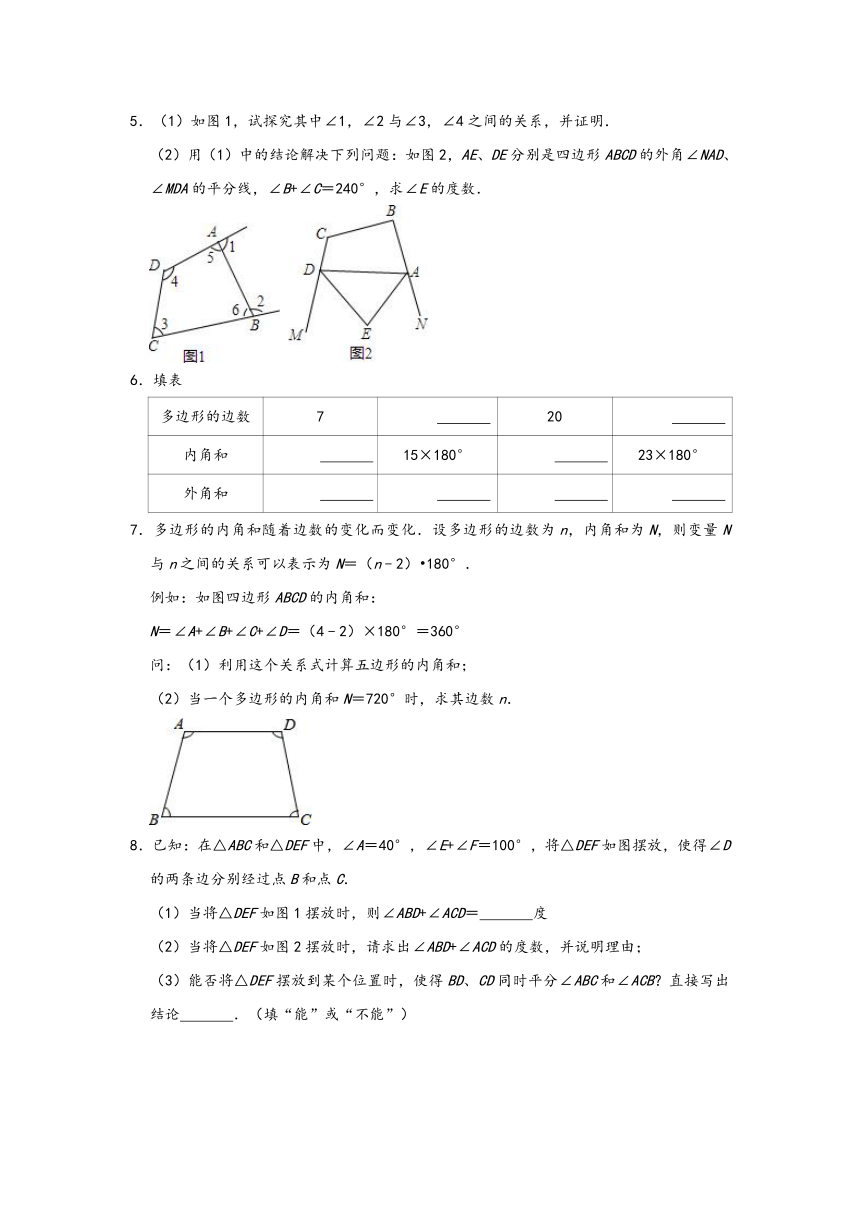
3.(1)如图1,设∠A=x,则∠1+∠2=
;
(2)把三角形纸片ABC顶角A沿DE折叠,点A落到点A'处,记∠A'DB为∠1,∠A'EC为∠2.
①如图2,∠1,∠2与∠A的数量关系是
;
②如图3,请你写出∠1,∠2与∠A的数量关系,并说明理由.
(3)如图4,把一个三角形纸片ABC的三个顶角分别向内折叠之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6=
.
4.如图,四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.
(1)试探究∠1与∠2有何关系,并说明理由.
(2)试探究BE与DF有何位置关系,并说明理由.
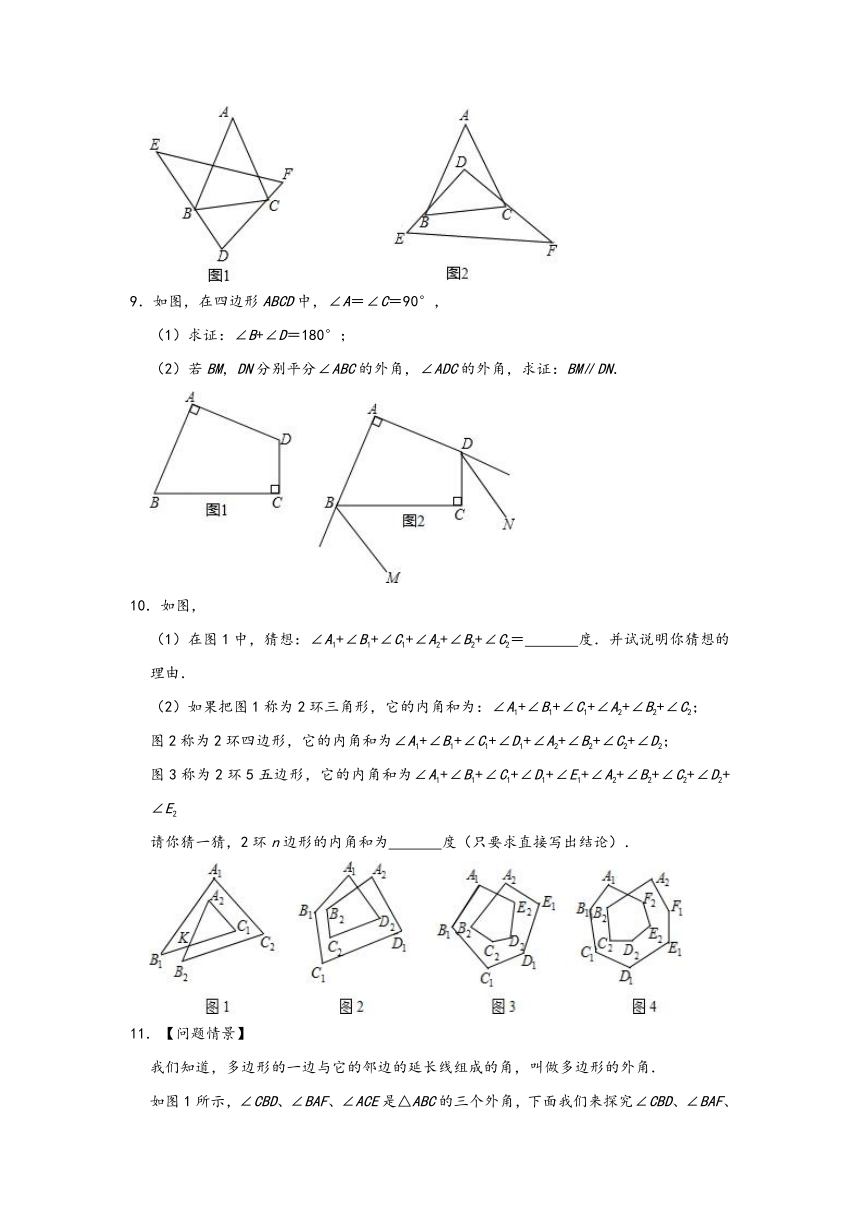
5.(1)如图1,试探究其中∠1,∠2与∠3,∠4之间的关系,并证明.
(2)用(1)中的结论解决下列问题:如图2,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
6.填表
多边形的边数
7
20
内角和
15×180°
23×180°
外角和
7.多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n﹣2)?180°.
例如:如图四边形ABCD的内角和:
N=∠A+∠B+∠C+∠D=(4﹣2)×180°=360°
问:(1)利用这个关系式计算五边形的内角和;
(2)当一个多边形的内角和N=720°时,求其边数n.
8.已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD=
度
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论
.(填“能”或“不能”)
9.如图,在四边形ABCD中,∠A=∠C=90°,
(1)求证:∠B+∠D=180°;
(2)若BM,DN分别平分∠ABC的外角,∠ADC的外角,求证:BM∥DN.
10.如图,
(1)在图1中,猜想:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=
度.并试说明你猜想的理由.
(2)如果把图1称为2环三角形,它的内角和为:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;
图2称为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;
图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1+∠A2+∠B2+∠C2+∠D2+∠E2
请你猜一猜,2环n边形的内角和为
度(只要求直接写出结论).
11.【问题情景】
我们知道,多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
如图1所示,∠CBD、∠BAF、∠ACE是△ABC的三个外角,下面我们来探究∠CBD、∠BAF、∠ACE和△ABC三内角之间的数量关系.
【方法感悟】
解:因为在△ABC中,
∠ABC+∠BAC+∠ACB=180°,
所以∠BAC+∠ACB=180°﹣∠ABC.
因为∠ABC+∠CBD=180°,
所以∠CBD=180°﹣∠ABC.
所以∠CBD=∠BAC+∠ACB.
同理可得:∠BAF=∠ABC+∠ACB,∠ACE=∠BAC+∠ABC.
因此,我们得到一个重要的结论:三角形的一个外角等于与它不相邻的两个内角的和.
【解决问题】
问题一:
已知:如图2,∠FDC与∠ECD分别为△ADC的两个外角,请直接利用上述结论,试探究∠FDC+∠ECD与∠A的数量关系.
问题二:
已知:如图3,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
问题三:
已知:如图4,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论直接写出∠P与∠A+∠B的数量关系.
.
12.探究多边形内角和时,我们常把多边形转化成三角形,再根据三角形内角为180°得出多边形内角和.如下图是探究多边形内角和一种方法,请根据图示,完成填空:
(1)四边形内角和:4×180°﹣2×180°=360°;
(2)五边形内角和:5×180°﹣2×180°=
;
(3)六边形内角和:6×180°﹣2×180°=
;
(4)n边形内角和:
=
.
13.如图,下列四边形是同一个四边形不断缩小(保持形状不变)的结果.
(1)在图中标出各个四边形的外角;
(2)在缩小的过程中,四边形对应的各个外角的大小是否发生了变化?
(3)如果保持四边形的形状不变,将四边形不断缩小下去,你能想象一下最终的形状吗?你能借助上面的变化过程说明四边形的外角和吗?
(4)你能类似地说明五边形、六边形……一般多边形的外角和吗?
14.阅读与推理
【阅读】三角形外角定理:三角形的外角等于与它不相邻的两个内角的和.例如在图中,∠ACD是△ABC的一个外角,则有∠ACD=∠A+∠B.
小明在课外书上看到这样一题:
“在五角星形ABCD中,求∠A+∠B+∠C+∠D+∠E的度数”.
小明思考:∠AFG是△FEC的外角,
根据“三角形外角定理”,可得∠AFE=∠
+∠
.
类似的,∠AGF是△BGD的外角,可得∠AGF=∠
+∠
.
小明已经有了解题思路,请你帮助他将这道题完整解答.
15.阅读下列材料:
求证:四边形的内角和等于360°.
已知:如图1所示,四边形ABCD.
求证:∠A+∠ABC+∠C+∠ADC=360°
证明:如图1所示,连接BD,在△ABD中,因为∠A+∠ABD+∠ADB=180°,在△CBD中,因为∠C+∠CBD+∠CDB=180°,所以∠A+∠ABD+∠ADB+∠C+∠CBD+∠CDB=180°+180°,即∠A+(∠ABD+∠CBD)+∠C+(∠ADB+∠CDB)=360°,所以∠A+∠ABC+∠C+∠ADC=360°.
解答下列问题:
(1)上述解题过程是通过作四边形的一条
,将四边形的内角和转化为
问题来得以解决;
(2)如图2所示,求证:∠A+∠B+∠C+∠D=360°.
参考答案
1.解:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣∠ADC﹣∠ACD,
=180°﹣(∠ADC+∠ACD),
=180°﹣(180°﹣∠A),
=90°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣∠ADC﹣∠BCD,
=180°﹣(∠ADC+∠BCD),
=180°﹣(360°﹣∠A﹣∠B),
=(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6﹣2)?180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD,
=180°﹣∠EDC﹣∠BCD,
=180°﹣(∠EDC+∠ACD),
=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=(∠A+∠B+∠E+∠F)﹣180°,
即∠P=(∠A+∠B+∠E+∠F)﹣180°.
2.解:(1)证明:【问题背景】在△AOB中,∠A+∠B+∠AOB=180°,在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)【尝试应用】)∵AP、CP分别平分∠BAD.∠BCD
∴∠1=∠2,∠3=∠4,
由(1)的结论得:,
①+②,得2∠P+∠1+∠3=∠2+∠4+∠B+∠D
∴∠P=(∠B+∠D)=26°.
(3)∠P=α+β.
3.解:(1)∠1+∠2=∠A+∠ACB+∠ABC+∠A=180°+x;
(2)①如图2,猜想:∠1+∠2=2∠A,理由是:
由折叠得:∠ADE=∠A′DE,∠AED=∠A′ED,
∵∠ADB+∠AEC=360°,
∴∠1+∠2=360°﹣∠ADE﹣∠A′DE﹣∠AED﹣∠A′ED=360°﹣2∠ADE﹣2∠AED,
∴∠1+∠2=2(180°﹣∠ADE﹣∠AED)=2∠A;
②如图3,∠1﹣∠2=2∠A,理由是:
∵∠1=∠AFE+∠A,∠AFE=∠A′+∠2,
∴∠1=∠A′+∠A+∠2,
∵∠A=∠A′,
∴∠1=2∠A+∠2,
∴∠1﹣∠2=2∠A;
(3)如图4,由题意知,
∠1+∠2+∠3+∠4+∠5+∠6=720°﹣(∠B'FG+∠B'GF)﹣(∠C'HI+∠C'IH)﹣(∠A'DE+∠A'ED)=720°﹣(180°﹣∠B')﹣(180°﹣C')﹣(180°﹣A')=180°+(∠B'+∠C'+∠A')
又∵∠B=∠B',∠C=∠C',∠A=∠A',
∠A+∠B+∠C=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6=360°.
故答案为:180°+x;∠1+∠2=2∠A;360°.
4.解:(1)∠1+∠2=90°;
∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°;
(2)BE∥DF;
在△FCD中,∵∠C=90°,
∴∠3+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠3,
∴BE∥DF.
5.解:(1)∠1+∠2=∠3+∠4.
理由:由四边形的内角和是360°可知:∠3+∠4+∠5+∠6=360°.
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2+∠5+∠6=360°.
∴∠1+∠2=∠3+∠4.
(2)由(1)可知∠MDA+∠DAN=∠B+∠C=240°.
∵AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,
∴∠EDA=∠MDA,∠EAD=∠DAN.
∴∠EDA+∠EAD=×(∠MDA+∠DAN)=×240°=120°.
6.解:填表如下:
多边形的边数
7
17
20
25
内角和
5×180°
15×180°
18×180°
23×180°
外角和
360°
360°
360°
360°
7.解:(1)N=(5﹣2)×180°=540°
(2)根据题意得:(n﹣2)×180°=720°
解得n=6.
8.解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°
∴∠ABC+∠ACB=180°﹣40°=140°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°﹣∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°﹣∠D
∴∠CBD+∠BCD=∠E+∠F=100°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°.
故答案为:240°;
(2)∠ABD+∠ACD=40°;
理由如下:
∵∠E+∠F=100°
∴∠D=180°﹣(∠E+∠F)=80°
∴∠ABD+∠ACD=180°﹣∠A﹣∠DBC﹣∠DCB
=180°﹣40°﹣(180°﹣80°)
=40°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
故答案为:不能.
9.(1)证明:∵∠A=∠C=90゜,
∴在四边形ABCD中,∠B+∠D=360°﹣∠A﹣∠C=180゜;
(2)解:如图2,连接BD,
∵∠ABC+∠ADC=180°,
∴∠FDC+∠EBC=180゜,
∵BM,DN分别平分∠ABC的外角,∠ADC的外角,
∴∠NDC+∠CBM=90゜,
∴∠NDC+∠CDB+∠CBD+∠MBC=180゜,
∴BM∥DN.
10.解:(1)连结B1B2,
则∠A2+∠C1=∠B1B2A2+∠B2B1C1,
∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=∠A1+∠B1+∠B1B2A2+∠B2B1C1+∠B2+∠C2=360度;
(2)如图,A1A2之间添加两条边,
可得∠B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2
则∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2=∠A1+∠B1+∠C1+∠D1+∠A2+∠EA1D+∠A1EA2+∠EA2B2=720°;
2环n边形添加(n﹣2)条边,2环n边形的内角和成为(2n﹣2)边形的内角和.其内角和为180(2n﹣4)=360(n﹣2)度.
故答案为:(1)360;(2)360(n﹣2)
11.解:(1)∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A.
(2)∵DP平分∠ADC,
∴∠PDC=∠ADC.
同理,∠PCD=∠ACD.
∴∠DPC=180°﹣∠PDC﹣∠PCD=180°﹣(180°﹣∠A)=90°+∠A;
(3)∵DP平分∠ADC,
∴∠PDC=∠ADC.
同理,∠PCD=∠BCD.
∴∠P=180°﹣∠PDC﹣∠PCD=180°﹣(360°﹣∠A﹣∠B)=(∠A+∠B).
故答案为:∠P=(∠A+∠B).
12.解:(1)四边形内角和:4×180°﹣2×180°=360°;
(2)五边形内角和:5×180°﹣2×180°=540°;
(3)六边形内角和:6×180°﹣2×180°=720°;
(4)n边形内角和:n×180°﹣2×180°=(n﹣2)×180°.
故答案为:(2)540°;(3)720°;(4)n×180°﹣2×180°,(n﹣2)×180°.
13.解:(1)如图所示:
(2)在缩小的过程中,四边形对应的各个外角的大小不变;
(3)如果保持四边形的形状不变,将四边形不断缩小下去,最终的形状是一个点,所以四边形的外角拼凑为一个周角.
∵四边形的内角和为:(4﹣2)×180°=360°,
∠1+∠BAD+∠2+∠ABC+∠3+∠BCD+∠4+∠CDA=4×180°=720°,
∴∠1+∠2+∠3+∠4=720°﹣(∠BAD+∠ABC+∠BCD+∠CDA)=720°﹣360°=360°,
即四边形的外角和为360°.
(4)如图所示:
∵五边形的内角和为:(5﹣2)×180°=540°,
∠1+∠BAE+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠DEA=5×180°=900°,
∴∠1+∠2+∠3+∠4+∠5=900°﹣(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)=900°﹣540°=360°,
即五边形的外角和为360°.
类似地,五边形、六边形……一般多边形的外角和等于360°.
14.解:在△CEF中,可得∠AFE=∠C+∠E,
在△BDG中,可得,AGF=∠B+∠D,
∴∠A+∠B+∠C+∠D+∠E=∠AFG+AGF+∠A=180°;
故答案为:E,C,B,D.
15.(1)解:上述解题过程是通过作四边形的一条对角线,
将四边形的内角和转化为三角形的内角和问题来得以解决.
(2)证明:如图2,
,
根据三角形的外角的性质,可得
∠ADE=∠ABE+∠A,
∠CDE=∠CBE+∠C,
∴∠ABE+∠CBE+∠A+∠C=∠ADE+∠CDE=∠ADC,
又∵∠ABE+∠CBE=∠ABC,
∴∠A+∠B+∠C=∠ADC,
∴∠A+∠B+∠C+∠D=360°.
故答案为:对角线、三角形的内角和.
11.3多边形习题
1.动手操作,探究:
探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究二:若将△ADC改为任意四边形ABCD呢?
已知:如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.(写出说理过程)
探究三:若将上题中的四边形ABCD改为六边形ABCDEF(图(3))呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:
.
2.【问题背景】小明在学习多边形时,把如图1的图形成为“8”字形,并得出如下结论:∠A+∠B=∠C+∠D,请你说明理由;
(2)【尝试应用】如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的
度数;
小明结合(1)中的结论并利用方程思想轻松解答如下:
解:由AP、CP分别平分∠BAD、∠BCD,可设∠1=∠2=x,∠3=∠4=y,
由(1)的结论得:,①+②,
得2∠P+x+y=x+y+∠B+∠D
∴(∠B+∠D)=26°
(3)【拓展延伸】如图3,已知∠C=α,∠B=β,∠CAP=∠CAB,∠CDP=∠CDB,请利用上述结论或方
法求∠P的度数.
3.(1)如图1,设∠A=x,则∠1+∠2=
;
(2)把三角形纸片ABC顶角A沿DE折叠,点A落到点A'处,记∠A'DB为∠1,∠A'EC为∠2.
①如图2,∠1,∠2与∠A的数量关系是
;
②如图3,请你写出∠1,∠2与∠A的数量关系,并说明理由.
(3)如图4,把一个三角形纸片ABC的三个顶角分别向内折叠之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6=
.
4.如图,四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.
(1)试探究∠1与∠2有何关系,并说明理由.
(2)试探究BE与DF有何位置关系,并说明理由.
5.(1)如图1,试探究其中∠1,∠2与∠3,∠4之间的关系,并证明.
(2)用(1)中的结论解决下列问题:如图2,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
6.填表
多边形的边数
7
20
内角和
15×180°
23×180°
外角和
7.多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n﹣2)?180°.
例如:如图四边形ABCD的内角和:
N=∠A+∠B+∠C+∠D=(4﹣2)×180°=360°
问:(1)利用这个关系式计算五边形的内角和;
(2)当一个多边形的内角和N=720°时,求其边数n.
8.已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD=
度
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论
.(填“能”或“不能”)
9.如图,在四边形ABCD中,∠A=∠C=90°,
(1)求证:∠B+∠D=180°;
(2)若BM,DN分别平分∠ABC的外角,∠ADC的外角,求证:BM∥DN.
10.如图,
(1)在图1中,猜想:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=
度.并试说明你猜想的理由.
(2)如果把图1称为2环三角形,它的内角和为:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;
图2称为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;
图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1+∠A2+∠B2+∠C2+∠D2+∠E2
请你猜一猜,2环n边形的内角和为
度(只要求直接写出结论).
11.【问题情景】
我们知道,多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
如图1所示,∠CBD、∠BAF、∠ACE是△ABC的三个外角,下面我们来探究∠CBD、∠BAF、∠ACE和△ABC三内角之间的数量关系.
【方法感悟】
解:因为在△ABC中,
∠ABC+∠BAC+∠ACB=180°,
所以∠BAC+∠ACB=180°﹣∠ABC.
因为∠ABC+∠CBD=180°,
所以∠CBD=180°﹣∠ABC.
所以∠CBD=∠BAC+∠ACB.
同理可得:∠BAF=∠ABC+∠ACB,∠ACE=∠BAC+∠ABC.
因此,我们得到一个重要的结论:三角形的一个外角等于与它不相邻的两个内角的和.
【解决问题】
问题一:
已知:如图2,∠FDC与∠ECD分别为△ADC的两个外角,请直接利用上述结论,试探究∠FDC+∠ECD与∠A的数量关系.
问题二:
已知:如图3,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
问题三:
已知:如图4,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论直接写出∠P与∠A+∠B的数量关系.
.
12.探究多边形内角和时,我们常把多边形转化成三角形,再根据三角形内角为180°得出多边形内角和.如下图是探究多边形内角和一种方法,请根据图示,完成填空:
(1)四边形内角和:4×180°﹣2×180°=360°;
(2)五边形内角和:5×180°﹣2×180°=
;
(3)六边形内角和:6×180°﹣2×180°=
;
(4)n边形内角和:
=
.
13.如图,下列四边形是同一个四边形不断缩小(保持形状不变)的结果.
(1)在图中标出各个四边形的外角;
(2)在缩小的过程中,四边形对应的各个外角的大小是否发生了变化?
(3)如果保持四边形的形状不变,将四边形不断缩小下去,你能想象一下最终的形状吗?你能借助上面的变化过程说明四边形的外角和吗?
(4)你能类似地说明五边形、六边形……一般多边形的外角和吗?
14.阅读与推理
【阅读】三角形外角定理:三角形的外角等于与它不相邻的两个内角的和.例如在图中,∠ACD是△ABC的一个外角,则有∠ACD=∠A+∠B.
小明在课外书上看到这样一题:
“在五角星形ABCD中,求∠A+∠B+∠C+∠D+∠E的度数”.
小明思考:∠AFG是△FEC的外角,
根据“三角形外角定理”,可得∠AFE=∠
+∠
.
类似的,∠AGF是△BGD的外角,可得∠AGF=∠
+∠
.
小明已经有了解题思路,请你帮助他将这道题完整解答.
15.阅读下列材料:
求证:四边形的内角和等于360°.
已知:如图1所示,四边形ABCD.
求证:∠A+∠ABC+∠C+∠ADC=360°
证明:如图1所示,连接BD,在△ABD中,因为∠A+∠ABD+∠ADB=180°,在△CBD中,因为∠C+∠CBD+∠CDB=180°,所以∠A+∠ABD+∠ADB+∠C+∠CBD+∠CDB=180°+180°,即∠A+(∠ABD+∠CBD)+∠C+(∠ADB+∠CDB)=360°,所以∠A+∠ABC+∠C+∠ADC=360°.
解答下列问题:
(1)上述解题过程是通过作四边形的一条
,将四边形的内角和转化为
问题来得以解决;
(2)如图2所示,求证:∠A+∠B+∠C+∠D=360°.
参考答案
1.解:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣∠ADC﹣∠ACD,
=180°﹣(∠ADC+∠ACD),
=180°﹣(180°﹣∠A),
=90°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣∠ADC﹣∠BCD,
=180°﹣(∠ADC+∠BCD),
=180°﹣(360°﹣∠A﹣∠B),
=(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6﹣2)?180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD,
=180°﹣∠EDC﹣∠BCD,
=180°﹣(∠EDC+∠ACD),
=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=(∠A+∠B+∠E+∠F)﹣180°,
即∠P=(∠A+∠B+∠E+∠F)﹣180°.
2.解:(1)证明:【问题背景】在△AOB中,∠A+∠B+∠AOB=180°,在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)【尝试应用】)∵AP、CP分别平分∠BAD.∠BCD
∴∠1=∠2,∠3=∠4,
由(1)的结论得:,
①+②,得2∠P+∠1+∠3=∠2+∠4+∠B+∠D
∴∠P=(∠B+∠D)=26°.
(3)∠P=α+β.
3.解:(1)∠1+∠2=∠A+∠ACB+∠ABC+∠A=180°+x;
(2)①如图2,猜想:∠1+∠2=2∠A,理由是:
由折叠得:∠ADE=∠A′DE,∠AED=∠A′ED,
∵∠ADB+∠AEC=360°,
∴∠1+∠2=360°﹣∠ADE﹣∠A′DE﹣∠AED﹣∠A′ED=360°﹣2∠ADE﹣2∠AED,
∴∠1+∠2=2(180°﹣∠ADE﹣∠AED)=2∠A;
②如图3,∠1﹣∠2=2∠A,理由是:
∵∠1=∠AFE+∠A,∠AFE=∠A′+∠2,
∴∠1=∠A′+∠A+∠2,
∵∠A=∠A′,
∴∠1=2∠A+∠2,
∴∠1﹣∠2=2∠A;
(3)如图4,由题意知,
∠1+∠2+∠3+∠4+∠5+∠6=720°﹣(∠B'FG+∠B'GF)﹣(∠C'HI+∠C'IH)﹣(∠A'DE+∠A'ED)=720°﹣(180°﹣∠B')﹣(180°﹣C')﹣(180°﹣A')=180°+(∠B'+∠C'+∠A')
又∵∠B=∠B',∠C=∠C',∠A=∠A',
∠A+∠B+∠C=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6=360°.
故答案为:180°+x;∠1+∠2=2∠A;360°.
4.解:(1)∠1+∠2=90°;
∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°;
(2)BE∥DF;
在△FCD中,∵∠C=90°,
∴∠3+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠3,
∴BE∥DF.
5.解:(1)∠1+∠2=∠3+∠4.
理由:由四边形的内角和是360°可知:∠3+∠4+∠5+∠6=360°.
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2+∠5+∠6=360°.
∴∠1+∠2=∠3+∠4.
(2)由(1)可知∠MDA+∠DAN=∠B+∠C=240°.
∵AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,
∴∠EDA=∠MDA,∠EAD=∠DAN.
∴∠EDA+∠EAD=×(∠MDA+∠DAN)=×240°=120°.
6.解:填表如下:
多边形的边数
7
17
20
25
内角和
5×180°
15×180°
18×180°
23×180°
外角和
360°
360°
360°
360°
7.解:(1)N=(5﹣2)×180°=540°
(2)根据题意得:(n﹣2)×180°=720°
解得n=6.
8.解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°
∴∠ABC+∠ACB=180°﹣40°=140°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°﹣∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°﹣∠D
∴∠CBD+∠BCD=∠E+∠F=100°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°.
故答案为:240°;
(2)∠ABD+∠ACD=40°;
理由如下:
∵∠E+∠F=100°
∴∠D=180°﹣(∠E+∠F)=80°
∴∠ABD+∠ACD=180°﹣∠A﹣∠DBC﹣∠DCB
=180°﹣40°﹣(180°﹣80°)
=40°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
故答案为:不能.
9.(1)证明:∵∠A=∠C=90゜,
∴在四边形ABCD中,∠B+∠D=360°﹣∠A﹣∠C=180゜;
(2)解:如图2,连接BD,
∵∠ABC+∠ADC=180°,
∴∠FDC+∠EBC=180゜,
∵BM,DN分别平分∠ABC的外角,∠ADC的外角,
∴∠NDC+∠CBM=90゜,
∴∠NDC+∠CDB+∠CBD+∠MBC=180゜,
∴BM∥DN.
10.解:(1)连结B1B2,
则∠A2+∠C1=∠B1B2A2+∠B2B1C1,
∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=∠A1+∠B1+∠B1B2A2+∠B2B1C1+∠B2+∠C2=360度;
(2)如图,A1A2之间添加两条边,
可得∠B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2
则∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2=∠A1+∠B1+∠C1+∠D1+∠A2+∠EA1D+∠A1EA2+∠EA2B2=720°;
2环n边形添加(n﹣2)条边,2环n边形的内角和成为(2n﹣2)边形的内角和.其内角和为180(2n﹣4)=360(n﹣2)度.
故答案为:(1)360;(2)360(n﹣2)
11.解:(1)∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A.
(2)∵DP平分∠ADC,
∴∠PDC=∠ADC.
同理,∠PCD=∠ACD.
∴∠DPC=180°﹣∠PDC﹣∠PCD=180°﹣(180°﹣∠A)=90°+∠A;
(3)∵DP平分∠ADC,
∴∠PDC=∠ADC.
同理,∠PCD=∠BCD.
∴∠P=180°﹣∠PDC﹣∠PCD=180°﹣(360°﹣∠A﹣∠B)=(∠A+∠B).
故答案为:∠P=(∠A+∠B).
12.解:(1)四边形内角和:4×180°﹣2×180°=360°;
(2)五边形内角和:5×180°﹣2×180°=540°;
(3)六边形内角和:6×180°﹣2×180°=720°;
(4)n边形内角和:n×180°﹣2×180°=(n﹣2)×180°.
故答案为:(2)540°;(3)720°;(4)n×180°﹣2×180°,(n﹣2)×180°.
13.解:(1)如图所示:
(2)在缩小的过程中,四边形对应的各个外角的大小不变;
(3)如果保持四边形的形状不变,将四边形不断缩小下去,最终的形状是一个点,所以四边形的外角拼凑为一个周角.
∵四边形的内角和为:(4﹣2)×180°=360°,
∠1+∠BAD+∠2+∠ABC+∠3+∠BCD+∠4+∠CDA=4×180°=720°,
∴∠1+∠2+∠3+∠4=720°﹣(∠BAD+∠ABC+∠BCD+∠CDA)=720°﹣360°=360°,
即四边形的外角和为360°.
(4)如图所示:
∵五边形的内角和为:(5﹣2)×180°=540°,
∠1+∠BAE+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠DEA=5×180°=900°,
∴∠1+∠2+∠3+∠4+∠5=900°﹣(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)=900°﹣540°=360°,
即五边形的外角和为360°.
类似地,五边形、六边形……一般多边形的外角和等于360°.
14.解:在△CEF中,可得∠AFE=∠C+∠E,
在△BDG中,可得,AGF=∠B+∠D,
∴∠A+∠B+∠C+∠D+∠E=∠AFG+AGF+∠A=180°;
故答案为:E,C,B,D.
15.(1)解:上述解题过程是通过作四边形的一条对角线,
将四边形的内角和转化为三角形的内角和问题来得以解决.
(2)证明:如图2,
,
根据三角形的外角的性质,可得
∠ADE=∠ABE+∠A,
∠CDE=∠CBE+∠C,
∴∠ABE+∠CBE+∠A+∠C=∠ADE+∠CDE=∠ADC,
又∵∠ABE+∠CBE=∠ABC,
∴∠A+∠B+∠C=∠ADC,
∴∠A+∠B+∠C+∠D=360°.
故答案为:对角线、三角形的内角和.
