2020-2021学年第一学期七年级数学(人教版)第一章《有理数》1.3有理数的加减法 当堂检测(word解析版)
文档属性
| 名称 | 2020-2021学年第一学期七年级数学(人教版)第一章《有理数》1.3有理数的加减法 当堂检测(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 287.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 12:09:57 | ||
图片预览




文档简介
2020-2021学年度第一学期七年级数学(人教版)第一章《有理数》1.3有理数的加减法当堂检测
学校:___________姓名:___________班级:___________分数:___________
一、选择题(本大题共12小题,共36.0分)
1.
若三个有理数的和为0,则( )
A.
三个数可能同号
B.
三个数一定为0
C.
一定有两个数互为相反数
D.
一定有一个数等于其余两个数的和的相反数
2.
-2-3+5的读法正确的是()
A.
负2、负3、正5的和
B.
负2、减3、正5的和
C.
负2、3、正5的和
D.
以上都不对
3.
比0小1的有理数是( )
A.
-1
B.
1
C.
0
D.
2
4.
式子-4-2-1+2的正确读法是( )
A.
减4减2减1加2
B.
负4减2减1加2
C.
-4,-2,-1加2
D.
4,2,1,2的和
5.
若()
-(-5)=-3,则括号内的数是()
A.
-2
B.
-8
C.
2
D.
8
6.
计算(-5)-(+3)+(-9)-(-7)所得的结果是()
A.
-9
B.
-10
C.
7
D.
-22
7.
下列各式中,与式子-1-2+3不相等的是()
A.
(-1)+(-2)+(+3)
B.
(-1)-2+(+3)
C.
(-1)+(-2)-(-3)
D.
(-1)-(-2)-(-3)
8.
式子-2-(-3)+(+1)-(-4)写成和的形式()
A.
-2+(+3)+(+1)+(-4)
B.
-2+(-3)+(+1)+(-4)
C.
-2+(+3)+(+1)+(+4)
D.
-2+(-3)+(+1)+(+4)
9.
下列算式计算正确的有()
①5+(-6)=-1;②-7+10=-3;③(-4)+(-5)=-9;④(-6.5)+0=-6.5.
A.
1个
B.
2个
C.
3个
D.
4个
10.
式子-3-7不能读作()
A.
-3与7的差
B.
-3与-7的和
C.
-3与-7的差
D.
-3减去7
11.
若()-(-
3)=4,则括号内的数是()
A.
-1
B.
1
C.
7
D.
-7
12.
下列判断中,正确的是()
A.
若a是有理数,则|a|-a=0一定成立
B.
两个有理数的和一定大于每个加数
C.
两个有理数的差一定小于被减数
D.
0减去任何数都等于这个数的相反数
二、填空题(本大题共5小题,共15.0分)
13.
已知两个数的和为,其中一个数为,则另一个数是________.
14.
算筹是我国古代的计算工具之一,也是中华民族智慧的结晶,如图①中用算筹表示的算式是“7408+2366”,则图②中算筹表示的算式的运算结果为________.
15.
已知|x|=7,|y|=2,且x16.
矿井下A、B两处的高度分别为-48米、-128米,A处比B处高________米.
17.
计算(+1)+(-2)+(+3)+(-4)+…+(+9)+(-10)的结果是________.
三、解答题(本大题共6小题,共48.0分)
18.
计算:
(1)(-8)-(+4)+(-7)-(+9);
(2);
(3);
(4).
19.
若a=6,b=2,c=-4,且a-b+(-c)-(-d)=1,求d的值.
20.
有一批罐头,现抽取10听样品进行检测,结果如下表(单位:g).
听号
1
2
3
4
5
6
7
8
9
10
质量
444
459
454
459
454
454
449
459
454
464
请你用简单的方法计算出这10听罐头的平均质量是多少.
21.
钟面上有1,2,3,…,11,12共12个数字.
(1)试在这些数前标上正,负号,使它们的和为0;
(2)在解题的过程中,你能总结什么规律?用文字叙述出来.
22.
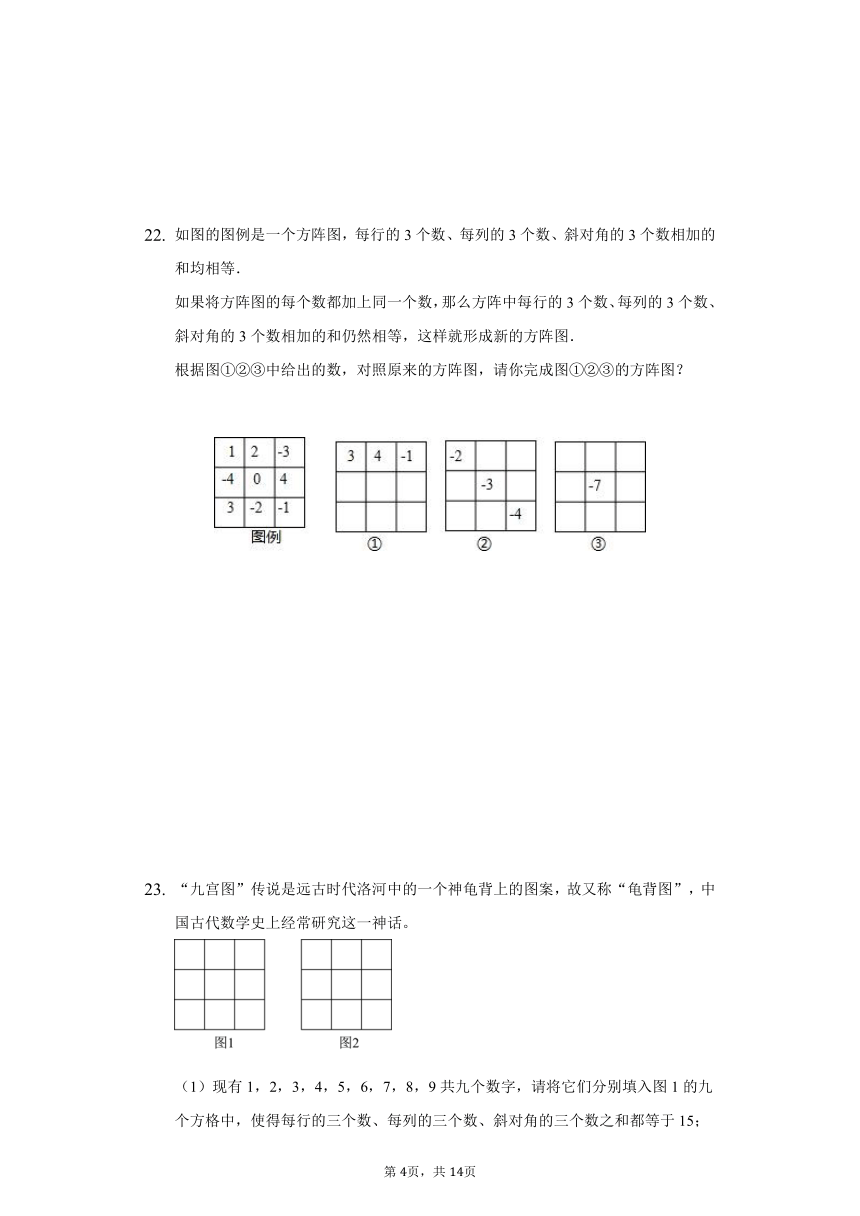
如图的图例是一个方阵图,每行的3个数、每列的3个数、斜对角的3个数相加的和均相等.
如果将方阵图的每个数都加上同一个数,那么方阵中每行的3个数、每列的3个数、斜对角的3个数相加的和仍然相等,这样就形成新的方阵图.
根据图①②③中给出的数,对照原来的方阵图,请你完成图①②③的方阵图?
23.
“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话。
?
(1)现有1,2,3,4,5,6,7,8,9共九个数字,请将它们分别填入图1的九个方格中,使得每行的三个数、每列的三个数、斜对角的三个数之和都等于15;
(2)通过研究问题(1),利用你发现的规律,将3,5,-7,1,7,-3,9,-5,-1这九个数字分别填入图2的九个方格中,使得横、竖、斜对角的所有三个数的和都相等。
答案和解析
1.【答案】D
【解析】
【分析】
本题考查有理数加法与相反数的知识.根据有理数加法与相反数的知识逐一判断即可求解.
【解答】
解:A、三个有理数同号时,相加后不改变符号,故A错误;
B、三个有理数不一定为0,故B错误;
?C、互为相反数相加得0,一定有一个数等于其余两个数的和的相反数,但不一定有两个数一定互为相反数,故C错误;
?D、互为相反数相加得0.
三个数相加得0,那么可先让其中的任意两个数相加,将问题转化为两个数相加,两个数相加为0,则这两个数互为相反数,故D正确;
故选D
.
2.【答案】A
【解析】
【分析】此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.原式利用运算法则变形,即可得到结果.
???????【解答】解:-2-3+5=(-2)+(-3)+5,读作:负2,负3,正5的和.
故选A.
3.【答案】A
【解析】解:由题意可得:0-1=-1,
故比0小1的有理数是:-1.
故选:A.
直接利用有理数的加减运算得出答案.
此题主要考查了有理数的加减运算,正确掌握运算法则是解题关键.
4.【答案】B
【解析】
【分析】
根据有理数的加法运算,可得出此式子表示-4,-2,-1,2的和,或者是负4减2减1加2即可.
?本题考查了有理数的加减混合运算,加法是减法的逆运算.
【解答】
解:式子-4-2-1+2的正确读法是:-4,-2,-1,2的和,或者是负4减2减1加2,
故选B.
5.【答案】B
【解析】
【分析】
本题考查了有理数减法,理解被减数、减数、差三者之间的关系是解题的关键.根据被减数等于差加减数列式计算即可得解.
【解答】
解:括号内的数=(-3)+(-5),
=-(3+5),
=-8.
故选B.
6.【答案】B
【解析】
【分析】
本题主要考查有理数加减混合运算的知识.根据减法法则把减法转化为加法,再用加法法则计算,得出结果.
【解答】
解:(-5)-(+3)+(-9)-(-7),
=(-5)+(-3)+(-9)+(+7),
=(-17)+(+7),
=-10.
故选B.
7.【答案】D
【解析】
【分析】
此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.各项去括号变形得到结果,即可做出判断.
【解答】
解:A.原式=-1-2+3,不合题意;
B.原式=-1-2+3,不合题意;
C.原式=-1-2+3,不合题意;
D.原式=-1+2+3,符合题意,
故选D.
8.【答案】C
【解析】解:原式=-2+(+3)+(+1)+(+4).
故选C
利用减法法则计算即可得到结果.
此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.
9.【答案】C
【解析】
【分析】
本题主要考查的是有理数的加法的有关知识,由题意利用有理数的加法法则对给出的各个选项进行逐一分析即可求解.
【解答】
解:5+(-6)=-1,故①正确;
-7+10=3,故②错误;
(-4)+(-5)=-9,故③正确;
(-6.5)+0=-6.5,故④正确.
则正确的有①③④,共3个.
?故选C.
10.【答案】C
【解析】
【分析】
本题考查了有理数的减法,有理数的加法,熟记读法是解题的关键.
根据有理数的加法与减法读法解答.
【解答】
解:
-3-7可以读作:-3与7的差,-3与-7的和,-3减去7,
不能读作:-3与-7的差.
故选C.
11.【答案】B
【解析】
【分析】
此题考查了有理数的加法,熟练掌握运算法则是解本题的关键.根据题意列出算式,计算即可得到结果.
【解答】
解:根据题意得:4+(-3)=1,
则1-(-3)=4,
故选B.
12.【答案】D
【解析】解:A、当a>0时,a的绝对值是它本身,当a<0时a的绝对值是它的相反数;
所以当a>0时,|a|-a=a-a=0;所以当a<0时,|a|-a=-a-a=-2a≠0.错误;
B、当两个加数都大于零时,两个有理数的和一定大于每个加数,例如2+3=5;
当两个加数都小于零时,两个有理数的和一定小于每个加数,例如(-2)+(-3)=-5.错误;
C、当减数大于零时,两个有理数的差一定小于被减数;例如3-2=1;
当减数小于零时,两个有理数的差一定大于被减数,例如5-(-3)=8;
当减数等于零时,两个有理数的差一定等于被减数,例如(-5)-0=-5.错误;
D、0-a=-a,正确.
故选D.
根据有理数的运算法则进行判断,同时要注意有理数有正负之分.
解决此类问题是要弄清减数与被减数的关系,同时要注意有理数有正负之分.
13.【答案】?
【解析】
【分析】
本题考查的是有理数的减法有关知识,根据题意列出算式,然后再进行计算即可解答.
【解答】
解:由题意可得:
.
答:另一个数为.
14.【答案】-426
【解析】
【分析】
根据题意和图示,可得算式103-529,然后求解.
此题考查了有理数的加法,关键是根据算筹表示出算式103-529.
【解答】
?103-529=-426.
故答案为:-426.
15.【答案】?-9或-5
【解析】
【分析】
本题考查了有理数的减法,绝对值的性质,是基础题,判断出x、y的对应情况是解题的关键.根据绝对值的性质求出x、y,然后判断出x、y的对应情况,再相减即可得解.
【解答】
解:∵|x|=7,|y|=2,
∴x=±7,y=±2,
∵x<y,
∴x=-7,y=±2,
∴x-y=-7-2=-9,
或x-y=-7-(-2)=-7+2=-5,
故答案为-9或-5.
16.【答案】80
【解析】
【分析】
本题考查的是有理数的减法有关知识,根据题意列出算式,即可解答.
【解答】
解:由题意可得:-48-(-128)=80.
答:A处比B处高80米.
?故答案为80.
17.【答案】-5
【解析】
【分析】
本题考查有理数的加法,先去掉括号,再找出规律,每两个数相加得-1,再乘以5,即可求出答案.
【解答】
解:(+1)+(-2)+(+3)+(-4)+…+(+9)+(-10)=1-2+3-4+5-6+…+9-10=(-1)×5=-5.
?故答案为-5.
18.【答案】解:(1)(-8)-(+4)+(-7)-(+9)
=-8-4-7-9
=-28;
(2)
=
=
=;
(3)
=
=
=;
(4)
=
=
=.
【解析】(1)根据有理数加减混合运算的方法解答即可;
(2)根据有理数加减混合运算的方法解答即可;
(3)根据有理数加减混合运算的方法解答即可;
(4)根据有理数加减混合运算的方法解答即可.
此题考查有理数的混合计算,关键是有理数加减混合运算方法解答.
19.【答案】解:∵a=6,b=2,c=-4,且a-b+(-c)-(-d)?=1,
∴6-2+[-(-4)]-(-d)=1,
即:6-2+4+d=1,
∴d=-7.
【解析】此题主要考查的是有理数的加法运算,掌握有理数的加法运算的法则,是解答此题的关键.根据题目的条件,代入数据,进行计算即可.
20.【答案】解:以450为基数,10听罐头与基准数的差距从左到右依次为:
-6,+9,+4,+9,+4,+4,-1,+9,+4,+14;
∴这10听罐头的总质量为:
(-6+9+4+9+4+4-1+9+4+14)+450×10
=50+4500
=4550(克).
∴这10听罐头的平均质量为:455010=455(克).
?答:这10听罐头的平均质量为455克.
【解析】此题主要考查正负数在实际生活中的应用.解题关键是理解“正”和“负”的相对性,选准基准数,弄清基准数、原数、浮动数之间的关系.以450为基数,高于450,记作“+”,那么低于450,应记作“-”,则与基准数的差距从左到右依次为:-6,+9,+4,+9,+4,+4,-1,+9,+4,+14.这10听罐头的总质量为:(-6+9+4+9+4+4-1+9+4+14)+450×10=50+4500=4550(克).
?这10听罐头的平均质量为:455010=455(克).
21.【答案】解:(1)-1-2-3-5-4+6-7-8-9+10+11+12;
(2)规律:先算出总和,再取半,在和为一半的数前加正号,其余的数前添负号.
【解析】先求出1,2,3,4,5,…,12这12个数的和为78,将78÷2得出5个正数绝对值的和为39,找到12个数中其余7个数绝对值的和等于39的数前面添加负号即可.
本题考查了有理数的加减混合运算.认真审题,找出规律:5个正数绝对值的和等于1,2,3,4,5,…,12这12个数的和的一半,是解决此题的关键所在.
22.【答案】解:(1)将图例中各数依次加上2,如图①;
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
(2)将图例中各数依次减去3,如图②;
(3)可将图例中各数依次减去7,如图③.
【解析】(1)图①中第一个数由图例中的1变为3,可将图例中各数依次加上2,填表即可;
(2)可将图例中各数依次减去3,填表即可;
(3)可将图例中各数依次减去7,填表即可.
本题考查了有理数的加法,九方格题目,趣味性较强,本题的关键是了解九方格的特点.
23.【答案】解:(1)15÷3=5,
∴最中间的数是5,其它空格填写如图1;
(2)如图2所示.
【解析】(1)根据每一个空格的数被使用3次,求出最中间的数是5,然后试探填入其它空格即可;
(2)先求出所有数的和是9,根据题意,每个数都用了3次,用9÷3=3得到横、竖、斜对角的所有三个数的和等于3,然后根据3试探填入数据即可.
本题考查了有理数加法,熟知“九宫图”的填法是解题的关键.
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________分数:___________
一、选择题(本大题共12小题,共36.0分)
1.
若三个有理数的和为0,则( )
A.
三个数可能同号
B.
三个数一定为0
C.
一定有两个数互为相反数
D.
一定有一个数等于其余两个数的和的相反数
2.
-2-3+5的读法正确的是()
A.
负2、负3、正5的和
B.
负2、减3、正5的和
C.
负2、3、正5的和
D.
以上都不对
3.
比0小1的有理数是( )
A.
-1
B.
1
C.
0
D.
2
4.
式子-4-2-1+2的正确读法是( )
A.
减4减2减1加2
B.
负4减2减1加2
C.
-4,-2,-1加2
D.
4,2,1,2的和
5.
若()
-(-5)=-3,则括号内的数是()
A.
-2
B.
-8
C.
2
D.
8
6.
计算(-5)-(+3)+(-9)-(-7)所得的结果是()
A.
-9
B.
-10
C.
7
D.
-22
7.
下列各式中,与式子-1-2+3不相等的是()
A.
(-1)+(-2)+(+3)
B.
(-1)-2+(+3)
C.
(-1)+(-2)-(-3)
D.
(-1)-(-2)-(-3)
8.
式子-2-(-3)+(+1)-(-4)写成和的形式()
A.
-2+(+3)+(+1)+(-4)
B.
-2+(-3)+(+1)+(-4)
C.
-2+(+3)+(+1)+(+4)
D.
-2+(-3)+(+1)+(+4)
9.
下列算式计算正确的有()
①5+(-6)=-1;②-7+10=-3;③(-4)+(-5)=-9;④(-6.5)+0=-6.5.
A.
1个
B.
2个
C.
3个
D.
4个
10.
式子-3-7不能读作()
A.
-3与7的差
B.
-3与-7的和
C.
-3与-7的差
D.
-3减去7
11.
若()-(-
3)=4,则括号内的数是()
A.
-1
B.
1
C.
7
D.
-7
12.
下列判断中,正确的是()
A.
若a是有理数,则|a|-a=0一定成立
B.
两个有理数的和一定大于每个加数
C.
两个有理数的差一定小于被减数
D.
0减去任何数都等于这个数的相反数
二、填空题(本大题共5小题,共15.0分)
13.
已知两个数的和为,其中一个数为,则另一个数是________.
14.
算筹是我国古代的计算工具之一,也是中华民族智慧的结晶,如图①中用算筹表示的算式是“7408+2366”,则图②中算筹表示的算式的运算结果为________.
15.
已知|x|=7,|y|=2,且x
矿井下A、B两处的高度分别为-48米、-128米,A处比B处高________米.
17.
计算(+1)+(-2)+(+3)+(-4)+…+(+9)+(-10)的结果是________.
三、解答题(本大题共6小题,共48.0分)
18.
计算:
(1)(-8)-(+4)+(-7)-(+9);
(2);
(3);
(4).
19.
若a=6,b=2,c=-4,且a-b+(-c)-(-d)=1,求d的值.
20.
有一批罐头,现抽取10听样品进行检测,结果如下表(单位:g).
听号
1
2
3
4
5
6
7
8
9
10
质量
444
459
454
459
454
454
449
459
454
464
请你用简单的方法计算出这10听罐头的平均质量是多少.
21.
钟面上有1,2,3,…,11,12共12个数字.
(1)试在这些数前标上正,负号,使它们的和为0;
(2)在解题的过程中,你能总结什么规律?用文字叙述出来.
22.
如图的图例是一个方阵图,每行的3个数、每列的3个数、斜对角的3个数相加的和均相等.
如果将方阵图的每个数都加上同一个数,那么方阵中每行的3个数、每列的3个数、斜对角的3个数相加的和仍然相等,这样就形成新的方阵图.
根据图①②③中给出的数,对照原来的方阵图,请你完成图①②③的方阵图?
23.
“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话。
?
(1)现有1,2,3,4,5,6,7,8,9共九个数字,请将它们分别填入图1的九个方格中,使得每行的三个数、每列的三个数、斜对角的三个数之和都等于15;
(2)通过研究问题(1),利用你发现的规律,将3,5,-7,1,7,-3,9,-5,-1这九个数字分别填入图2的九个方格中,使得横、竖、斜对角的所有三个数的和都相等。
答案和解析
1.【答案】D
【解析】
【分析】
本题考查有理数加法与相反数的知识.根据有理数加法与相反数的知识逐一判断即可求解.
【解答】
解:A、三个有理数同号时,相加后不改变符号,故A错误;
B、三个有理数不一定为0,故B错误;
?C、互为相反数相加得0,一定有一个数等于其余两个数的和的相反数,但不一定有两个数一定互为相反数,故C错误;
?D、互为相反数相加得0.
三个数相加得0,那么可先让其中的任意两个数相加,将问题转化为两个数相加,两个数相加为0,则这两个数互为相反数,故D正确;
故选D
.
2.【答案】A
【解析】
【分析】此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.原式利用运算法则变形,即可得到结果.
???????【解答】解:-2-3+5=(-2)+(-3)+5,读作:负2,负3,正5的和.
故选A.
3.【答案】A
【解析】解:由题意可得:0-1=-1,
故比0小1的有理数是:-1.
故选:A.
直接利用有理数的加减运算得出答案.
此题主要考查了有理数的加减运算,正确掌握运算法则是解题关键.
4.【答案】B
【解析】
【分析】
根据有理数的加法运算,可得出此式子表示-4,-2,-1,2的和,或者是负4减2减1加2即可.
?本题考查了有理数的加减混合运算,加法是减法的逆运算.
【解答】
解:式子-4-2-1+2的正确读法是:-4,-2,-1,2的和,或者是负4减2减1加2,
故选B.
5.【答案】B
【解析】
【分析】
本题考查了有理数减法,理解被减数、减数、差三者之间的关系是解题的关键.根据被减数等于差加减数列式计算即可得解.
【解答】
解:括号内的数=(-3)+(-5),
=-(3+5),
=-8.
故选B.
6.【答案】B
【解析】
【分析】
本题主要考查有理数加减混合运算的知识.根据减法法则把减法转化为加法,再用加法法则计算,得出结果.
【解答】
解:(-5)-(+3)+(-9)-(-7),
=(-5)+(-3)+(-9)+(+7),
=(-17)+(+7),
=-10.
故选B.
7.【答案】D
【解析】
【分析】
此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.各项去括号变形得到结果,即可做出判断.
【解答】
解:A.原式=-1-2+3,不合题意;
B.原式=-1-2+3,不合题意;
C.原式=-1-2+3,不合题意;
D.原式=-1+2+3,符合题意,
故选D.
8.【答案】C
【解析】解:原式=-2+(+3)+(+1)+(+4).
故选C
利用减法法则计算即可得到结果.
此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.
9.【答案】C
【解析】
【分析】
本题主要考查的是有理数的加法的有关知识,由题意利用有理数的加法法则对给出的各个选项进行逐一分析即可求解.
【解答】
解:5+(-6)=-1,故①正确;
-7+10=3,故②错误;
(-4)+(-5)=-9,故③正确;
(-6.5)+0=-6.5,故④正确.
则正确的有①③④,共3个.
?故选C.
10.【答案】C
【解析】
【分析】
本题考查了有理数的减法,有理数的加法,熟记读法是解题的关键.
根据有理数的加法与减法读法解答.
【解答】
解:
-3-7可以读作:-3与7的差,-3与-7的和,-3减去7,
不能读作:-3与-7的差.
故选C.
11.【答案】B
【解析】
【分析】
此题考查了有理数的加法,熟练掌握运算法则是解本题的关键.根据题意列出算式,计算即可得到结果.
【解答】
解:根据题意得:4+(-3)=1,
则1-(-3)=4,
故选B.
12.【答案】D
【解析】解:A、当a>0时,a的绝对值是它本身,当a<0时a的绝对值是它的相反数;
所以当a>0时,|a|-a=a-a=0;所以当a<0时,|a|-a=-a-a=-2a≠0.错误;
B、当两个加数都大于零时,两个有理数的和一定大于每个加数,例如2+3=5;
当两个加数都小于零时,两个有理数的和一定小于每个加数,例如(-2)+(-3)=-5.错误;
C、当减数大于零时,两个有理数的差一定小于被减数;例如3-2=1;
当减数小于零时,两个有理数的差一定大于被减数,例如5-(-3)=8;
当减数等于零时,两个有理数的差一定等于被减数,例如(-5)-0=-5.错误;
D、0-a=-a,正确.
故选D.
根据有理数的运算法则进行判断,同时要注意有理数有正负之分.
解决此类问题是要弄清减数与被减数的关系,同时要注意有理数有正负之分.
13.【答案】?
【解析】
【分析】
本题考查的是有理数的减法有关知识,根据题意列出算式,然后再进行计算即可解答.
【解答】
解:由题意可得:
.
答:另一个数为.
14.【答案】-426
【解析】
【分析】
根据题意和图示,可得算式103-529,然后求解.
此题考查了有理数的加法,关键是根据算筹表示出算式103-529.
【解答】
?103-529=-426.
故答案为:-426.
15.【答案】?-9或-5
【解析】
【分析】
本题考查了有理数的减法,绝对值的性质,是基础题,判断出x、y的对应情况是解题的关键.根据绝对值的性质求出x、y,然后判断出x、y的对应情况,再相减即可得解.
【解答】
解:∵|x|=7,|y|=2,
∴x=±7,y=±2,
∵x<y,
∴x=-7,y=±2,
∴x-y=-7-2=-9,
或x-y=-7-(-2)=-7+2=-5,
故答案为-9或-5.
16.【答案】80
【解析】
【分析】
本题考查的是有理数的减法有关知识,根据题意列出算式,即可解答.
【解答】
解:由题意可得:-48-(-128)=80.
答:A处比B处高80米.
?故答案为80.
17.【答案】-5
【解析】
【分析】
本题考查有理数的加法,先去掉括号,再找出规律,每两个数相加得-1,再乘以5,即可求出答案.
【解答】
解:(+1)+(-2)+(+3)+(-4)+…+(+9)+(-10)=1-2+3-4+5-6+…+9-10=(-1)×5=-5.
?故答案为-5.
18.【答案】解:(1)(-8)-(+4)+(-7)-(+9)
=-8-4-7-9
=-28;
(2)
=
=
=;
(3)
=
=
=;
(4)
=
=
=.
【解析】(1)根据有理数加减混合运算的方法解答即可;
(2)根据有理数加减混合运算的方法解答即可;
(3)根据有理数加减混合运算的方法解答即可;
(4)根据有理数加减混合运算的方法解答即可.
此题考查有理数的混合计算,关键是有理数加减混合运算方法解答.
19.【答案】解:∵a=6,b=2,c=-4,且a-b+(-c)-(-d)?=1,
∴6-2+[-(-4)]-(-d)=1,
即:6-2+4+d=1,
∴d=-7.
【解析】此题主要考查的是有理数的加法运算,掌握有理数的加法运算的法则,是解答此题的关键.根据题目的条件,代入数据,进行计算即可.
20.【答案】解:以450为基数,10听罐头与基准数的差距从左到右依次为:
-6,+9,+4,+9,+4,+4,-1,+9,+4,+14;
∴这10听罐头的总质量为:
(-6+9+4+9+4+4-1+9+4+14)+450×10
=50+4500
=4550(克).
∴这10听罐头的平均质量为:455010=455(克).
?答:这10听罐头的平均质量为455克.
【解析】此题主要考查正负数在实际生活中的应用.解题关键是理解“正”和“负”的相对性,选准基准数,弄清基准数、原数、浮动数之间的关系.以450为基数,高于450,记作“+”,那么低于450,应记作“-”,则与基准数的差距从左到右依次为:-6,+9,+4,+9,+4,+4,-1,+9,+4,+14.这10听罐头的总质量为:(-6+9+4+9+4+4-1+9+4+14)+450×10=50+4500=4550(克).
?这10听罐头的平均质量为:455010=455(克).
21.【答案】解:(1)-1-2-3-5-4+6-7-8-9+10+11+12;
(2)规律:先算出总和,再取半,在和为一半的数前加正号,其余的数前添负号.
【解析】先求出1,2,3,4,5,…,12这12个数的和为78,将78÷2得出5个正数绝对值的和为39,找到12个数中其余7个数绝对值的和等于39的数前面添加负号即可.
本题考查了有理数的加减混合运算.认真审题,找出规律:5个正数绝对值的和等于1,2,3,4,5,…,12这12个数的和的一半,是解决此题的关键所在.
22.【答案】解:(1)将图例中各数依次加上2,如图①;
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
(2)将图例中各数依次减去3,如图②;
(3)可将图例中各数依次减去7,如图③.
【解析】(1)图①中第一个数由图例中的1变为3,可将图例中各数依次加上2,填表即可;
(2)可将图例中各数依次减去3,填表即可;
(3)可将图例中各数依次减去7,填表即可.
本题考查了有理数的加法,九方格题目,趣味性较强,本题的关键是了解九方格的特点.
23.【答案】解:(1)15÷3=5,
∴最中间的数是5,其它空格填写如图1;
(2)如图2所示.
【解析】(1)根据每一个空格的数被使用3次,求出最中间的数是5,然后试探填入其它空格即可;
(2)先求出所有数的和是9,根据题意,每个数都用了3次,用9÷3=3得到横、竖、斜对角的所有三个数的和等于3,然后根据3试探填入数据即可.
本题考查了有理数加法,熟知“九宫图”的填法是解题的关键.
第2页,共2页
第1页,共1页
