北师大版八年级数学上册第三章位置与坐标同步测试(Word版 含答案)
文档属性
| 名称 | 北师大版八年级数学上册第三章位置与坐标同步测试(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 111.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 14:56:16 | ||
图片预览


文档简介
北师大版八年级数学上册
第三章位置与坐标
同步测试
一.选择题
1.根据下列表述,能确定位置的是( )
A.光明剧院2排
B.某市人民路
C.北偏东40°
D.东经112°,北纬36°
2.若点A(a+1,b﹣2)在第二象限,则点B(﹣a,1﹣b)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.平面直角坐标系中,点A在第四象限,点A到x轴的距离为2,到y轴的距离为3,则点A的坐标为( )
A.(2,﹣3)
B.(﹣3,2)
C.(3,﹣2)
D.(﹣2,3)
4.已知点P坐标(2-a,3a+6)且点P到两坐标轴的距离相等,则点P坐标是
(
)
A.(3,3)
B.(3,-3)
C.(6,-6)
D.(3,3)或(6,-6)
5.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )
A.y轴对称
B.x轴对称
C.原点对称
D.直线y=x对称
6.已知点A(a,2017)与点A′(﹣2018,b)是关于原点O的对称点,则a+b的值为( )
A.1
B.5
C.6
D.4
7.无论m为何值,点A(m,5﹣2m)不可能在(?).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.点A(a,4),点B(3,b)关于x轴对称,则(a+b)2013的值为
( )
A.0
B.-1
C.1
D.72013
9.如图,已知在边长为2的等边三角形EFG中,以边EF所在直线为x轴建立适当的平面直角坐标系,得到点G的坐标为(1,3),则该坐标系的原点在( )
A.E点处
B.F点处
C.G点处
D.EF的中点处
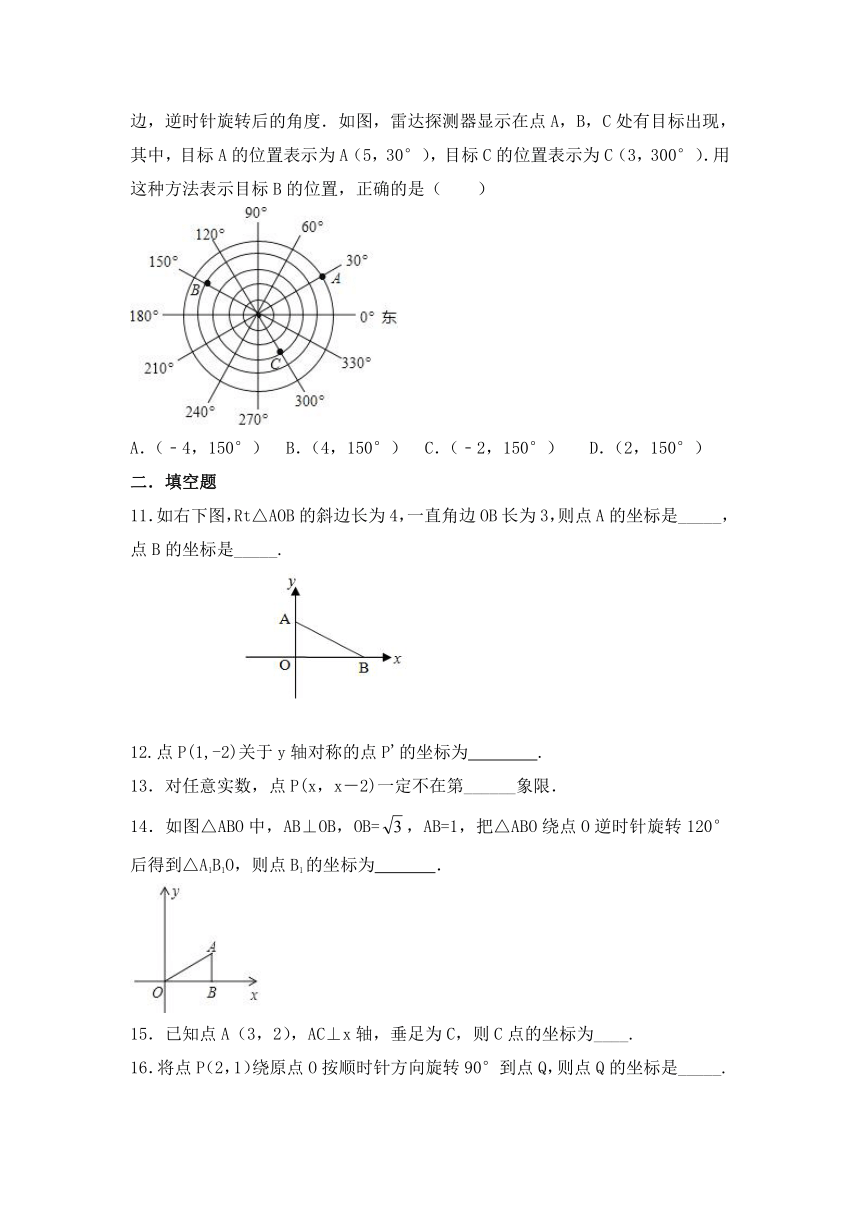
10.雷达二维平面定位的主要原理是:测量目标的两个信息﹣距离和角度,目标的表示方法为(m,α),其中,m表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标C的位置表示为C(3,300°).用这种方法表示目标B的位置,正确的是( )
A.(﹣4,150°)
B.(4,150°)
C.(﹣2,150°)
D.(2,150°)
二.填空题
11.如右下图,Rt△AOB的斜边长为4,一直角边OB长为3,则点A的坐标是_____,点B的坐标是_____.
12.点P(1,-2)关于y轴对称的点P'的坐标为 .?
13.对任意实数,点P(x,x-2)一定不在第______象限.
14.如图△ABO中,AB⊥OB,OB=,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为
.
15.已知点A(3,2),AC⊥x轴,垂足为C,则C点的坐标为____.
16.将点P(2,1)绕原点O按顺时针方向旋转90°到点Q,则点Q的坐标是_____.
17.如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是________.
18.一个小球从点A(3,3)出发,经过y轴上点C反弹后经过点B(1,0),则小球从A点经过点C到B点经过的最短路线长是
.
三.解答题
19.如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使点A的坐标为(-2,4),点B的坐标为(-4,2);
(2)在第二象限内的格点上找一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,画出△ABC,则点C的坐标是________,△ABC的周长是________(结果保留根号);
(3)作出△ABC关于x轴对称的△A′B′C′.
20.如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别是A(0,0),B(7,0),C(9,5),D(2,7).
(1)在坐标系中,画出此四边形;
(2)求此四边形的面积.
如图所示,四边形ABCD各个顶点的坐标分别为A(-2,8),B(-11,6),C(-14,0),D(0,0).
(1)确定这个四边形的面积,你是怎么做的?(写出一种做法即可)
(2)如果把A,B,C,D各点的纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
22.在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
(1)填表:
P从O点出发时间
可得到整数点的坐标
可得到整数点的个数
1秒
(0,1).(1,0)
2
2秒
?
?
3秒
?
?
(2)当P点从点O出发10秒,可得到的整数点的个数是______个.
(3)当P点从点O出发______秒时,可得到整数点(10,5)
23.(1)在平面直角坐标系中,将点A(-3,4)向右平移5个单位长度到点A1,再将点A1绕坐标原点顺时针旋转90°到点A2,求点A1,A2的坐标;
(2)在平面直角坐标系中,将第二象限内的点B(a,b)向右平移m个单位长度得到第一象限内的点B1,再将点B1绕坐标原点顺时针旋转90°到点B2,写出点B1,B2的坐标;
24.下面的方格纸中画出了一个“小猪”的图案,已知每个小正方形的边长为1.
(1)“小猪”所占的面积为多少?
(2)在上面的方格纸中作出“小猪”关于直线DE对称的图案(只画图,不写作法);
(3)以G为原点,GE所在直线为x轴,GB所在直线为y轴,小正方形的边长为单位长度建立平面直角坐标系,可得点A的坐标是(__________,__________).
答案提示
1.D 2.D.3.C.4.D
5.B
6.A.7.C.8.B
9.A 10.B.
11.
(3,0)?12.(-1,-2)
13.二
14.(﹣,).15.(3,0)
16.(1,-2)
17.(4,2)或(-4,2)或(-4,3)
18.5
19.解:(1)如图所示
(2)如图所示.
(-1,1);2+2
(3)如图所示.
20.解:(1)四边形ABCD如图所示;
(2)四边形的面积=9×7﹣×2×7﹣×2×5﹣×2×7,
=63﹣7﹣5﹣7,
=63﹣19,
=44.
21.解:(1)80,可分割成直角三角形和长方形求面积.(答案不唯一) (2)80.
22.解:(1)以1秒时达到的整数点为基准,向上或向右移动一格得到2秒时的可能的整数点;再以2秒时得到的整数点为基准,向上或向右移动一格,得到3秒时可能得到的整数点.
P从O点出发时间
可得到整数点的坐标
可得到整数点的个数
1秒
(0,1).(1,0)
2
2秒
(0,2),(2,0),(1,1)
3
3秒
(0,3),(3,0),(2,1),(1,2)
4
(2)1秒时,达到2个整数点;2秒时,达到3个整数点;3秒时,达到4个整数点,那么10秒时,应达到11个整数点;
(3)横坐标为10,需要从原点开始沿x轴向右移动10秒,纵坐标为5,需再向上移动5秒,所以需要的时间为15秒.
23.解:(1)∵将点A(-3,4)向右平移5个单位长度到点A1,∴点A1的坐标为(2,4),∵又将点A1绕坐标原点顺时针旋转90°到点A2,∴A2的坐标为(4,-2). (2)根据(1)中的规律,得B1的坐标为(a+m,b),B2的坐标为(b,-a-m).
24.解:(1)观察图形:“小猪”所占面积包括29个小正方形和7个小三角形面积和,每个小三角形面积是小正方形面积的一半,所以“小猪”所占面积为32.5.
(2)“小猪”关于直线DE对称的图案如图所示.
(3)点A的坐标是(-4,1).
第三章位置与坐标
同步测试
一.选择题
1.根据下列表述,能确定位置的是( )
A.光明剧院2排
B.某市人民路
C.北偏东40°
D.东经112°,北纬36°
2.若点A(a+1,b﹣2)在第二象限,则点B(﹣a,1﹣b)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.平面直角坐标系中,点A在第四象限,点A到x轴的距离为2,到y轴的距离为3,则点A的坐标为( )
A.(2,﹣3)
B.(﹣3,2)
C.(3,﹣2)
D.(﹣2,3)
4.已知点P坐标(2-a,3a+6)且点P到两坐标轴的距离相等,则点P坐标是
(
)
A.(3,3)
B.(3,-3)
C.(6,-6)
D.(3,3)或(6,-6)
5.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )
A.y轴对称
B.x轴对称
C.原点对称
D.直线y=x对称
6.已知点A(a,2017)与点A′(﹣2018,b)是关于原点O的对称点,则a+b的值为( )
A.1
B.5
C.6
D.4
7.无论m为何值,点A(m,5﹣2m)不可能在(?).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.点A(a,4),点B(3,b)关于x轴对称,则(a+b)2013的值为
( )
A.0
B.-1
C.1
D.72013
9.如图,已知在边长为2的等边三角形EFG中,以边EF所在直线为x轴建立适当的平面直角坐标系,得到点G的坐标为(1,3),则该坐标系的原点在( )
A.E点处
B.F点处
C.G点处
D.EF的中点处
10.雷达二维平面定位的主要原理是:测量目标的两个信息﹣距离和角度,目标的表示方法为(m,α),其中,m表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为A(5,30°),目标C的位置表示为C(3,300°).用这种方法表示目标B的位置,正确的是( )
A.(﹣4,150°)
B.(4,150°)
C.(﹣2,150°)
D.(2,150°)
二.填空题
11.如右下图,Rt△AOB的斜边长为4,一直角边OB长为3,则点A的坐标是_____,点B的坐标是_____.
12.点P(1,-2)关于y轴对称的点P'的坐标为 .?
13.对任意实数,点P(x,x-2)一定不在第______象限.
14.如图△ABO中,AB⊥OB,OB=,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为
.
15.已知点A(3,2),AC⊥x轴,垂足为C,则C点的坐标为____.
16.将点P(2,1)绕原点O按顺时针方向旋转90°到点Q,则点Q的坐标是_____.
17.如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是________.
18.一个小球从点A(3,3)出发,经过y轴上点C反弹后经过点B(1,0),则小球从A点经过点C到B点经过的最短路线长是
.
三.解答题
19.如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使点A的坐标为(-2,4),点B的坐标为(-4,2);
(2)在第二象限内的格点上找一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,画出△ABC,则点C的坐标是________,△ABC的周长是________(结果保留根号);
(3)作出△ABC关于x轴对称的△A′B′C′.
20.如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别是A(0,0),B(7,0),C(9,5),D(2,7).
(1)在坐标系中,画出此四边形;
(2)求此四边形的面积.
如图所示,四边形ABCD各个顶点的坐标分别为A(-2,8),B(-11,6),C(-14,0),D(0,0).
(1)确定这个四边形的面积,你是怎么做的?(写出一种做法即可)
(2)如果把A,B,C,D各点的纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
22.在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
(1)填表:
P从O点出发时间
可得到整数点的坐标
可得到整数点的个数
1秒
(0,1).(1,0)
2
2秒
?
?
3秒
?
?
(2)当P点从点O出发10秒,可得到的整数点的个数是______个.
(3)当P点从点O出发______秒时,可得到整数点(10,5)
23.(1)在平面直角坐标系中,将点A(-3,4)向右平移5个单位长度到点A1,再将点A1绕坐标原点顺时针旋转90°到点A2,求点A1,A2的坐标;
(2)在平面直角坐标系中,将第二象限内的点B(a,b)向右平移m个单位长度得到第一象限内的点B1,再将点B1绕坐标原点顺时针旋转90°到点B2,写出点B1,B2的坐标;
24.下面的方格纸中画出了一个“小猪”的图案,已知每个小正方形的边长为1.
(1)“小猪”所占的面积为多少?
(2)在上面的方格纸中作出“小猪”关于直线DE对称的图案(只画图,不写作法);
(3)以G为原点,GE所在直线为x轴,GB所在直线为y轴,小正方形的边长为单位长度建立平面直角坐标系,可得点A的坐标是(__________,__________).
答案提示
1.D 2.D.3.C.4.D
5.B
6.A.7.C.8.B
9.A 10.B.
11.
(3,0)?12.(-1,-2)
13.二
14.(﹣,).15.(3,0)
16.(1,-2)
17.(4,2)或(-4,2)或(-4,3)
18.5
19.解:(1)如图所示
(2)如图所示.
(-1,1);2+2
(3)如图所示.
20.解:(1)四边形ABCD如图所示;
(2)四边形的面积=9×7﹣×2×7﹣×2×5﹣×2×7,
=63﹣7﹣5﹣7,
=63﹣19,
=44.
21.解:(1)80,可分割成直角三角形和长方形求面积.(答案不唯一) (2)80.
22.解:(1)以1秒时达到的整数点为基准,向上或向右移动一格得到2秒时的可能的整数点;再以2秒时得到的整数点为基准,向上或向右移动一格,得到3秒时可能得到的整数点.
P从O点出发时间
可得到整数点的坐标
可得到整数点的个数
1秒
(0,1).(1,0)
2
2秒
(0,2),(2,0),(1,1)
3
3秒
(0,3),(3,0),(2,1),(1,2)
4
(2)1秒时,达到2个整数点;2秒时,达到3个整数点;3秒时,达到4个整数点,那么10秒时,应达到11个整数点;
(3)横坐标为10,需要从原点开始沿x轴向右移动10秒,纵坐标为5,需再向上移动5秒,所以需要的时间为15秒.
23.解:(1)∵将点A(-3,4)向右平移5个单位长度到点A1,∴点A1的坐标为(2,4),∵又将点A1绕坐标原点顺时针旋转90°到点A2,∴A2的坐标为(4,-2). (2)根据(1)中的规律,得B1的坐标为(a+m,b),B2的坐标为(b,-a-m).
24.解:(1)观察图形:“小猪”所占面积包括29个小正方形和7个小三角形面积和,每个小三角形面积是小正方形面积的一半,所以“小猪”所占面积为32.5.
(2)“小猪”关于直线DE对称的图案如图所示.
(3)点A的坐标是(-4,1).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
