人教版八年级数学上册同步练习题 : 11.3多边形及其内角和(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册同步练习题 : 11.3多边形及其内角和(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 288.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 23:29:16 | ||
图片预览

文档简介
人教版八年级数学上册同步练习题
第十一章三角形
11.3多边形及其内角和
一、选择题
1.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是
A.8
B.9
C.10
D.12
2.马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于,则该多边形的边数是( )
A.7
B.8
C.7或8
D.无法确定
3.(题型四)过多边形的一个顶点作一条直线,把这个多边形截去两个角后,它的内角和为1
260°,则这个多边形为(
)
A.十边形
B.十一边形
C.十二边形
D.十边形或十一边形
4.在凸多边形中,四边形有两条对角线,五边形有5条对角线.观察探索凸十边形有(
)条对角线.
A.29
B.32
C.35
D.38
5.如果一个多边形的每一个内角都相等,且每一个内角的度数为135°,那么这个多边形的边数为(
)
A.6
B.7
C.8
D.以上答案都不对
6.如果一个多边形的边数增加1,那么它的内角和增加(
).
A.0°
B.90°
C.180°
D.360°
7.如果一个四边形四个内角度数之比是2∶2∶3∶5,那么这四个内角中(
).
A.只有一个直角
B.只有一个锐角
C.有两个直角
D.有两个钝角
8.从十二边形的一个顶点出发可引_________条对角线,把十二边形分成_______个三角形.
A.9
10
B.10
11
C.11
12
D.12
13
9.若凸n边形的每个外角都是36°,则从一个顶点出发引的对角线条数是(??
)
A.6
B.7
C.8
D.9
10.一个多边形的内角和是外角和的5倍,那么这个多边形的边数是(
)
A.10
B.12
C.6
D.7
二、填空题
11.过m边形的一个顶点有7条对角线,n边形没有对角线,则m+n是________.
12.在四边形ABCD中,若∠A∶∠B∶∠C∶∠D=3∶1∶2∶3,则该四边形中最大的角的度数是____.
13.把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状可能是_________边形.
14.若一个正多边形的内角和2340°,则边数为___.它的外角等于___.
15.四边形有2条对角线,五边形有5条对角线,六边形有9条对角线,……n边形有________条对角线.
三、解答题
16.已知一个多边形的内角和与一个外角的差为1560°,求这个多边形的边数和这个外角的度数.
17.在四边形中,,
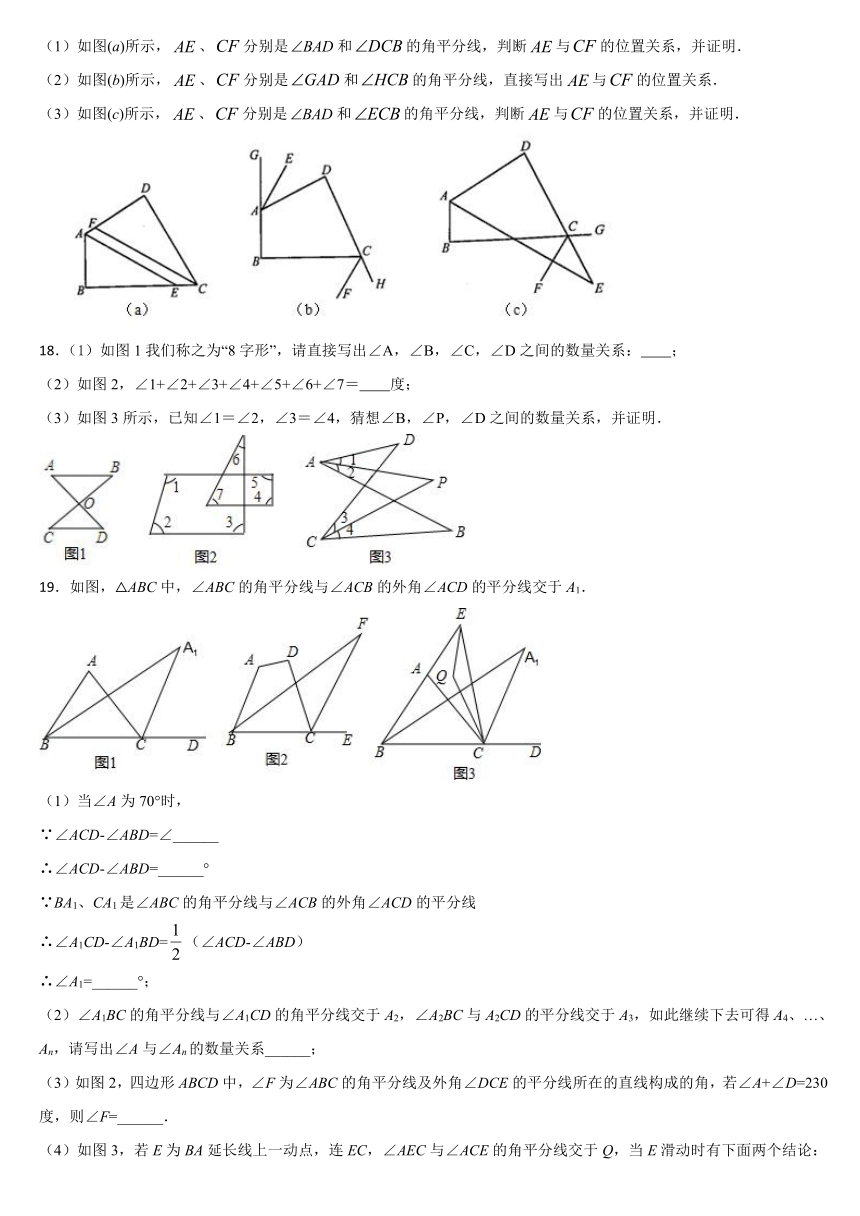
(1)如图(a)所示,、分别是和的角平分线,判断与的位置关系,并证明.
(2)如图(b)所示,、分别是和的角平分线,直接写出与的位置关系.
(3)如图(c)所示,、分别是和的角平分线,判断与的位置关系,并证明.
18.(1)如图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系: ;
(2)如图2,∠1+∠2+∠3+∠4+∠5+∠6+∠7= 度;
(3)如图3所示,已知∠1=∠2,∠3=∠4,猜想∠B,∠P,∠D之间的数量关系,并证明.
19.如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
(1)当∠A为70°时,
∵∠ACD-∠ABD=∠______
∴∠ACD-∠ABD=______°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD-∠A1BD=(∠ACD-∠ABD)
∴∠A1=______°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An的数量关系______;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F=______.
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q-∠A1的值为定值.其中有且只有一个是正确的,请写出正确的结论,并求出其值.
20.(1)如图(1)所示是四边形,小明作出它对角线为2条,算法为=2.
(2)如图(2)是五边形,小明作出它的对角线有5条,算法为=5.
(3)如图(3)是六边形,可以作出它的对角线有________条,算法为________.
(4)猜想边数为n的多边形对角线条数的算法及条数.
21.已知一个多边形的内角和与外角和的和为1080°,且这个多边形的各个内角都相等.求这个多边形的每个外角度数.
22.我们已经证明了“三角形的内角等于180°”,易证“四边形的内角和等于360°=2×180°,五边形的内角和等于540°=3×180°……”试猜想一下十边形的内角等于多少度?n边形的内角和等于多少度?
23.如果一个凸多边形除了一个内角以外,其它内角的和为2570°,求这个没有计算在内的内角的度数.
【参考答案】
1.A
2.C
3.D
4.C
5.C
7.A
8.A
9.B
10.B
11.13
12.120°
13.三、四、五
14.
十五
24°
15.
16.11
,60°.
17.(1).证明过程如下:
如图1,∵
∴
又∵、分别是、的角平分线
∴
∵
∴
∴;
(2).证明过程如下:
如图2,连接AC
由(1)知,
是的角平分线
同理可得:
即
又,即
,即
;
(3).证明过程如下:
如图3,设与相交于点
由(1)知,
∵
∴
∵、分别是和的角平分线
∴,
∴
∵
∴
∴.
18.(1)∠A+∠B=∠C+∠D;(2)540°;(3)2∠P=∠D+∠B.
19.(1)∠A;70°;35°;
(2)∠A=2n∠An
(3)25°
(4)①∠Q+∠A1的值为定值正确,Q+∠A1=180°.
20.(3)9,=9;(4).
21.60°.
22.十边形的内角和1440°,n边形的内角和:(n-2)×180°.
23.130°
第十一章三角形
11.3多边形及其内角和
一、选择题
1.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是
A.8
B.9
C.10
D.12
2.马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于,则该多边形的边数是( )
A.7
B.8
C.7或8
D.无法确定
3.(题型四)过多边形的一个顶点作一条直线,把这个多边形截去两个角后,它的内角和为1
260°,则这个多边形为(
)
A.十边形
B.十一边形
C.十二边形
D.十边形或十一边形
4.在凸多边形中,四边形有两条对角线,五边形有5条对角线.观察探索凸十边形有(
)条对角线.
A.29
B.32
C.35
D.38
5.如果一个多边形的每一个内角都相等,且每一个内角的度数为135°,那么这个多边形的边数为(
)
A.6
B.7
C.8
D.以上答案都不对
6.如果一个多边形的边数增加1,那么它的内角和增加(
).
A.0°
B.90°
C.180°
D.360°
7.如果一个四边形四个内角度数之比是2∶2∶3∶5,那么这四个内角中(
).
A.只有一个直角
B.只有一个锐角
C.有两个直角
D.有两个钝角
8.从十二边形的一个顶点出发可引_________条对角线,把十二边形分成_______个三角形.
A.9
10
B.10
11
C.11
12
D.12
13
9.若凸n边形的每个外角都是36°,则从一个顶点出发引的对角线条数是(??
)
A.6
B.7
C.8
D.9
10.一个多边形的内角和是外角和的5倍,那么这个多边形的边数是(
)
A.10
B.12
C.6
D.7
二、填空题
11.过m边形的一个顶点有7条对角线,n边形没有对角线,则m+n是________.
12.在四边形ABCD中,若∠A∶∠B∶∠C∶∠D=3∶1∶2∶3,则该四边形中最大的角的度数是____.
13.把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状可能是_________边形.
14.若一个正多边形的内角和2340°,则边数为___.它的外角等于___.
15.四边形有2条对角线,五边形有5条对角线,六边形有9条对角线,……n边形有________条对角线.
三、解答题
16.已知一个多边形的内角和与一个外角的差为1560°,求这个多边形的边数和这个外角的度数.
17.在四边形中,,
(1)如图(a)所示,、分别是和的角平分线,判断与的位置关系,并证明.
(2)如图(b)所示,、分别是和的角平分线,直接写出与的位置关系.
(3)如图(c)所示,、分别是和的角平分线,判断与的位置关系,并证明.
18.(1)如图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系: ;
(2)如图2,∠1+∠2+∠3+∠4+∠5+∠6+∠7= 度;
(3)如图3所示,已知∠1=∠2,∠3=∠4,猜想∠B,∠P,∠D之间的数量关系,并证明.
19.如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
(1)当∠A为70°时,
∵∠ACD-∠ABD=∠______
∴∠ACD-∠ABD=______°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD-∠A1BD=(∠ACD-∠ABD)
∴∠A1=______°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An的数量关系______;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F=______.
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q-∠A1的值为定值.其中有且只有一个是正确的,请写出正确的结论,并求出其值.
20.(1)如图(1)所示是四边形,小明作出它对角线为2条,算法为=2.
(2)如图(2)是五边形,小明作出它的对角线有5条,算法为=5.
(3)如图(3)是六边形,可以作出它的对角线有________条,算法为________.
(4)猜想边数为n的多边形对角线条数的算法及条数.
21.已知一个多边形的内角和与外角和的和为1080°,且这个多边形的各个内角都相等.求这个多边形的每个外角度数.
22.我们已经证明了“三角形的内角等于180°”,易证“四边形的内角和等于360°=2×180°,五边形的内角和等于540°=3×180°……”试猜想一下十边形的内角等于多少度?n边形的内角和等于多少度?
23.如果一个凸多边形除了一个内角以外,其它内角的和为2570°,求这个没有计算在内的内角的度数.
【参考答案】
1.A
2.C
3.D
4.C
5.C
7.A
8.A
9.B
10.B
11.13
12.120°
13.三、四、五
14.
十五
24°
15.
16.11
,60°.
17.(1).证明过程如下:
如图1,∵
∴
又∵、分别是、的角平分线
∴
∵
∴
∴;
(2).证明过程如下:
如图2,连接AC
由(1)知,
是的角平分线
同理可得:
即
又,即
,即
;
(3).证明过程如下:
如图3,设与相交于点
由(1)知,
∵
∴
∵、分别是和的角平分线
∴,
∴
∵
∴
∴.
18.(1)∠A+∠B=∠C+∠D;(2)540°;(3)2∠P=∠D+∠B.
19.(1)∠A;70°;35°;
(2)∠A=2n∠An
(3)25°
(4)①∠Q+∠A1的值为定值正确,Q+∠A1=180°.
20.(3)9,=9;(4).
21.60°.
22.十边形的内角和1440°,n边形的内角和:(n-2)×180°.
23.130°
