人教版数学七上1.3-1.4有理数的加减、乘除运算 复习学案及练习
文档属性
| 名称 | 人教版数学七上1.3-1.4有理数的加减、乘除运算 复习学案及练习 |  | |
| 格式 | zip | ||
| 文件大小 | 144.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 13:18:41 | ||
图片预览



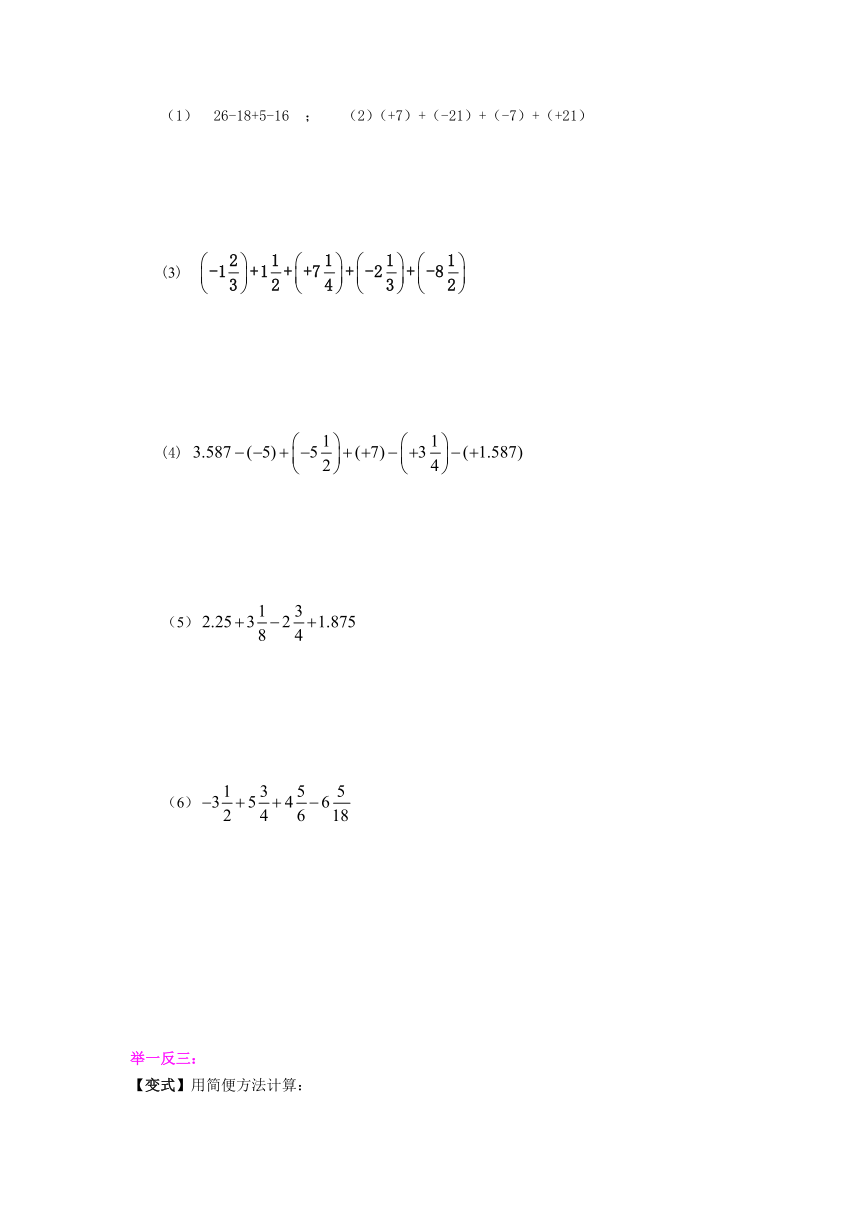

文档简介
【学习目标】
1.掌握有理数加减乘除法的法则和运算技巧,理解运算符号和性质符号的意义
2.
巩固倒数的概念,能进行简单有理数的加、减、乘、除混合运算;
3.
培养观察、分析、归纳及运算能力.
【要点梳理】
要点一、有理数的加法
1.定义:把两个有理数合成一个有理数的运算叫作有理数的加法.
2.法则:(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0;
(3)一个数同0相加,仍得这个数.
要点诠释:利用法则进行加法运算的步骤:
(1)判断两个加数的符号是同号、异号,还是有一个加数为零,以此来选择用哪条法则.
(2)确定和的符号(是“+”还是“-”).
(3)求各加数的绝对值,并确定和的绝对值(加数的绝对值是相加还是相减).
3.运算律:
有理数加法运算律
加法交换律
文字语言
两个数相加,交换加数的位置,和不变
符号语言
a+b=b+a
加法结合律
文字语言
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变
符号语言
(a+b)+c=a+(b+c)
要点诠释:交换加数的位置时,不要忘记符号.
要点二、有理数的减法
1.定义:
已知两个数的和与其中一个加数,求另一个加数的运算,叫做减法,例如:(-5)+?=7,求?,减法是加法的逆运算.
要点诠释:(1)任意两个数都可以进行减法运算.
(2)
几个有理数相减,差仍为有理数,差由两部分组成:①性质符号;②数字即数的绝对值.
2.法则:减去一个数,等于加这个数的相反数,即有:.
要点诠释:
将减法转化为加法时,注意同时进行的两变,一变是减法变加法;二变是把减数变为它的相反数”.如:
要点三、有理数加减混合运算
将加减法统一成加法运算,适当应用加法运算律简化计算.
要点四、有理数的乘法
1.有理数的乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘;
(2)任何数同0相乘,都得0.
要点诠释:
(1)
不为0的两数相乘,先确定符号,再把绝对值相乘.
(2)当因数中有负号时,必须用括号括起来,如-2与-3的乘积,应列为(-2)×(-3),不应该写成-2×-3.
2.
有理数的乘法法则的推广:(1)几个不等于0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积为负;当负因数的个数有偶数个时,积为正;
(2)几个数相乘,如果有一个因数为0,那么积就等于0.
要点诠释:(1)在有理数的乘法中,每一个乘数都叫做一个因数.
(2)几个不等于0的有理数相乘,先根据负因数的个数确定积的符号,然后把各因数的绝对值相乘.
(3)几个数相乘,如果有一个因数为0,那么积就等于0.反之,如果积为0,那么至少有一个因数为0.
3.
有理数的乘法运算律:
(1)乘法交换律:两个数相乘,交换因数的位置,积相等,即:ab=ba.
(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.即:abc=(ab)c=a(bc).
(3)乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.即:a(b+c)=ab+ac.
要点诠释:
(1)在交换因数的位置时,要连同符号一起交换.
(2)乘法运算律可推广为:三个以上的有理数相乘,可以任意交换因数的位置,或者把其中的几个因数相乘.如abcd=d(ac)b.一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.如a(b+c+d)=ab+ac+ad.
(3)运用运算律的目的是“简化运算”,有时,根据需要可以把运算律“顺用”,也可以把运算律“逆用”.
要点五、有理数的除法
1.倒数的意义:
乘积是1的两个数互为倒数.
要点诠释:(1)“互为倒数”的两个数是互相依存的.如-2的倒数是,-2和是互相依存的;
(2)0和任何数相乘都不等于1,因此0没有倒数;
(3)倒数的结果必须化成最简形式,使分母中不含小数和分数;
(4)互为倒数的两个数必定同号(同为正数或同为负数).
2.
有理数除法法则:
法则一:除以一个不等于0的数,等于乘这个数的倒数,即.
法则二:两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.
要点诠释:(1)一般在不能整除的情况下应用法则一,在能整除时应用法则二方便些.
(2)因为0没有倒数,所以0不能当除数.
(3)法则二与有理数乘法法则相似,两数相除时先确定商的符号,再确定商的绝对值.
要点六、有理数的乘除混合运算
由于乘除是同一级运算,应按从左往右的顺序计算,一般先将除法化成乘法,然后确定积的符号,最后算出结果.
要点七、有理数的加减乘除混合运算
有理数的加减乘除混合运算,如无括号,则按照“先乘除,后加减”的顺序进行,如有括号,则先算括号里面的.
【典型例题】-有理数的加减法
类型一、有理数的加法运算
例1.计算:
(+20)+(+12);
(2);
(3)(+2)+(-11);
(4)(-3.4)+(+4.3);
(5)(-5)+0.
举一反三:
【变式1】计算:
类型二、有理数的减法运算
例2.
计算:(1)(-32)-(+5);
(2)(+2)-(-25).
举一反三:
【变式】若( )﹣(﹣2)=3,则括号内的数是( )
A.
﹣1
B.
1
C.
5
D.
﹣5
类型三、有理数的加减混合运算
例3.计算,能用简便方法的用简便方法计算.
(1)
26-18+5-16
;
(2)(+7)+(-21)+(-7)+(+21)
(3)
(4)
(5)
(6)
举一反三:
【变式】用简便方法计算:
(1)(-2.4)+(-4.2)+(-3.8)+(+3.1)+(+0.8)+(-0.7)
(2)
2
类型四、有理数的加减混合运算在实际中的应用
例4.邮递员骑车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1cm表示1km,画出数轴,并在该数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)邮递员一共骑了多少千米?
举一反三:
【变式1】华英中学七年级(14)班的学生分成五组进行答题游戏,每组的基本分为100分,答对一题加50分,答错一题扣50分,游戏结束后各组的得分如下表:
第1组
第2组
第3组
第4组
第5组
100
150
350
-400
-100
(1)第一名超过第二名多少分?
(2)第一名超过第五名多少分?
【变式2】某产粮专业户出售粮食8袋,每袋重量(单位:千克)如下:
197,202,197,203,200,196,201,198.
计算出售的粮食总共多少千克?
【典型例题】
类型一、有理数的乘法运算
例1.算式(﹣1)×(﹣3)×之值为何?( )
A.
B.
C.
D.
例2.
(1);
(2)(1-2)(2-3)(3-4)…(19-20);
(3)(-5)×(-8.1)×3.14×0.
例3.运用简便方法计算:
(2)(-0.25)×0.5×(-100)×4
(3)
举一反三:
【变式1】计算16.8×+7.6×的结果是 .
【变式2】;
类型二、有理数的除法运算
例4.计算:(1)(-32)÷(-8)
(2)
举一反三:
【变式】
计算:(1)
类型三:有理数的乘除混合运算
例5.计算:
【变式1】计算:(-9)÷(-4)÷(-2)
【变式2】计算:(1)
(2)
类型四、有理数的加减乘除混合运算
例6.
计算(1);
(2)
【变式】
类型五:利用有理数的加减乘除,解决实际问题
例7.气象统计资料表明,高度每增加1000米,气温就降低6℃.如果现在地面的气温是27℃,那么8000米的高空的气温大约是多少?
课后作业
一、选择题
1.某市2020年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高(
).
A.-10℃
B.-6℃
C.6℃
D.10℃
2.若等式0□1=﹣1成立,则□内的运算符号为( )
A.
+
B.
﹣
C.
×
D.
÷
3.两个有理数相加,和小于其中一个加数而大于另一个加数,需满足
(
)
A.两个数都是正数
B.两个数都是负数
C.一个是正数,另一个是负数
D.至少有一个数是零
4.某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差
(
)
A.0.8kg
B.0.6kg
C.0.5kg
D.0.4kg
5.下列命题中,正确的是(
).
A.若a·b>0,则a>0,b>0
B.若a·b>0,则a<0,b<0
C.若a·b=0,则a=0且b=0
D.若a·b=0,则a=0或b=0
6.
下列说法错误的是
(
)
A.一个数与1相乘仍得这个数.
B.互为相反数(除0外)的两个数的商为-1.
C.一个数与-1相乘得这个数的相反数.
D.互为倒数的两个数的商为1.
7.
下列计算:①0-(-5)=-5;②;③;④;⑤若,则x的倒数是6.其中正确的个数是(
).
A.1
B.2
C.3
D.4
二、填空题
8.
计算:|﹣2|+2=________.(﹣6)×(﹣)= .
9.某月股票M开盘价20元,上午10点跌1.6元,下午收盘时又涨了0.4元,则股票这天的收盘价是_______.
10.若,则
0,
0,
0.
11.
若|a|=5,b=-2,且a÷b>0,则a+b=________.
如果6个不等于0的数相乘得积为负数,则在这6个乘数中,正的乘数有
个
13.在-2,3,4,-5这四个数中,任取两个数相乘所得积最大的是
,所得的商最小是
。
14.
是一个简单的数值运算程序,当输入-1时,则输出的数值____.
三、解答题
15.计算题
(1)
(2)
(3)(-0.125)×(-18)×(-8)×0×(-1)
(4)(-6)×45+(-6)×55
(5)
(6)
16.
某人用400元购买了8套儿童服装,准备以一定价格出售,如果以每套儿童服装55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,﹣3,+2,+1,﹣2,﹣1,0,﹣2.(单位:元)
(1)当他卖完这八套儿童服装后是盈利还是亏损?
(2)盈利(或亏损)了多少钱?
1.掌握有理数加减乘除法的法则和运算技巧,理解运算符号和性质符号的意义
2.
巩固倒数的概念,能进行简单有理数的加、减、乘、除混合运算;
3.
培养观察、分析、归纳及运算能力.
【要点梳理】
要点一、有理数的加法
1.定义:把两个有理数合成一个有理数的运算叫作有理数的加法.
2.法则:(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0;
(3)一个数同0相加,仍得这个数.
要点诠释:利用法则进行加法运算的步骤:
(1)判断两个加数的符号是同号、异号,还是有一个加数为零,以此来选择用哪条法则.
(2)确定和的符号(是“+”还是“-”).
(3)求各加数的绝对值,并确定和的绝对值(加数的绝对值是相加还是相减).
3.运算律:
有理数加法运算律
加法交换律
文字语言
两个数相加,交换加数的位置,和不变
符号语言
a+b=b+a
加法结合律
文字语言
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变
符号语言
(a+b)+c=a+(b+c)
要点诠释:交换加数的位置时,不要忘记符号.
要点二、有理数的减法
1.定义:
已知两个数的和与其中一个加数,求另一个加数的运算,叫做减法,例如:(-5)+?=7,求?,减法是加法的逆运算.
要点诠释:(1)任意两个数都可以进行减法运算.
(2)
几个有理数相减,差仍为有理数,差由两部分组成:①性质符号;②数字即数的绝对值.
2.法则:减去一个数,等于加这个数的相反数,即有:.
要点诠释:
将减法转化为加法时,注意同时进行的两变,一变是减法变加法;二变是把减数变为它的相反数”.如:
要点三、有理数加减混合运算
将加减法统一成加法运算,适当应用加法运算律简化计算.
要点四、有理数的乘法
1.有理数的乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘;
(2)任何数同0相乘,都得0.
要点诠释:
(1)
不为0的两数相乘,先确定符号,再把绝对值相乘.
(2)当因数中有负号时,必须用括号括起来,如-2与-3的乘积,应列为(-2)×(-3),不应该写成-2×-3.
2.
有理数的乘法法则的推广:(1)几个不等于0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积为负;当负因数的个数有偶数个时,积为正;
(2)几个数相乘,如果有一个因数为0,那么积就等于0.
要点诠释:(1)在有理数的乘法中,每一个乘数都叫做一个因数.
(2)几个不等于0的有理数相乘,先根据负因数的个数确定积的符号,然后把各因数的绝对值相乘.
(3)几个数相乘,如果有一个因数为0,那么积就等于0.反之,如果积为0,那么至少有一个因数为0.
3.
有理数的乘法运算律:
(1)乘法交换律:两个数相乘,交换因数的位置,积相等,即:ab=ba.
(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.即:abc=(ab)c=a(bc).
(3)乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.即:a(b+c)=ab+ac.
要点诠释:
(1)在交换因数的位置时,要连同符号一起交换.
(2)乘法运算律可推广为:三个以上的有理数相乘,可以任意交换因数的位置,或者把其中的几个因数相乘.如abcd=d(ac)b.一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.如a(b+c+d)=ab+ac+ad.
(3)运用运算律的目的是“简化运算”,有时,根据需要可以把运算律“顺用”,也可以把运算律“逆用”.
要点五、有理数的除法
1.倒数的意义:
乘积是1的两个数互为倒数.
要点诠释:(1)“互为倒数”的两个数是互相依存的.如-2的倒数是,-2和是互相依存的;
(2)0和任何数相乘都不等于1,因此0没有倒数;
(3)倒数的结果必须化成最简形式,使分母中不含小数和分数;
(4)互为倒数的两个数必定同号(同为正数或同为负数).
2.
有理数除法法则:
法则一:除以一个不等于0的数,等于乘这个数的倒数,即.
法则二:两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.
要点诠释:(1)一般在不能整除的情况下应用法则一,在能整除时应用法则二方便些.
(2)因为0没有倒数,所以0不能当除数.
(3)法则二与有理数乘法法则相似,两数相除时先确定商的符号,再确定商的绝对值.
要点六、有理数的乘除混合运算
由于乘除是同一级运算,应按从左往右的顺序计算,一般先将除法化成乘法,然后确定积的符号,最后算出结果.
要点七、有理数的加减乘除混合运算
有理数的加减乘除混合运算,如无括号,则按照“先乘除,后加减”的顺序进行,如有括号,则先算括号里面的.
【典型例题】-有理数的加减法
类型一、有理数的加法运算
例1.计算:
(+20)+(+12);
(2);
(3)(+2)+(-11);
(4)(-3.4)+(+4.3);
(5)(-5)+0.
举一反三:
【变式1】计算:
类型二、有理数的减法运算
例2.
计算:(1)(-32)-(+5);
(2)(+2)-(-25).
举一反三:
【变式】若( )﹣(﹣2)=3,则括号内的数是( )
A.
﹣1
B.
1
C.
5
D.
﹣5
类型三、有理数的加减混合运算
例3.计算,能用简便方法的用简便方法计算.
(1)
26-18+5-16
;
(2)(+7)+(-21)+(-7)+(+21)
(3)
(4)
(5)
(6)
举一反三:
【变式】用简便方法计算:
(1)(-2.4)+(-4.2)+(-3.8)+(+3.1)+(+0.8)+(-0.7)
(2)
2
类型四、有理数的加减混合运算在实际中的应用
例4.邮递员骑车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1cm表示1km,画出数轴,并在该数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)邮递员一共骑了多少千米?
举一反三:
【变式1】华英中学七年级(14)班的学生分成五组进行答题游戏,每组的基本分为100分,答对一题加50分,答错一题扣50分,游戏结束后各组的得分如下表:
第1组
第2组
第3组
第4组
第5组
100
150
350
-400
-100
(1)第一名超过第二名多少分?
(2)第一名超过第五名多少分?
【变式2】某产粮专业户出售粮食8袋,每袋重量(单位:千克)如下:
197,202,197,203,200,196,201,198.
计算出售的粮食总共多少千克?
【典型例题】
类型一、有理数的乘法运算
例1.算式(﹣1)×(﹣3)×之值为何?( )
A.
B.
C.
D.
例2.
(1);
(2)(1-2)(2-3)(3-4)…(19-20);
(3)(-5)×(-8.1)×3.14×0.
例3.运用简便方法计算:
(2)(-0.25)×0.5×(-100)×4
(3)
举一反三:
【变式1】计算16.8×+7.6×的结果是 .
【变式2】;
类型二、有理数的除法运算
例4.计算:(1)(-32)÷(-8)
(2)
举一反三:
【变式】
计算:(1)
类型三:有理数的乘除混合运算
例5.计算:
【变式1】计算:(-9)÷(-4)÷(-2)
【变式2】计算:(1)
(2)
类型四、有理数的加减乘除混合运算
例6.
计算(1);
(2)
【变式】
类型五:利用有理数的加减乘除,解决实际问题
例7.气象统计资料表明,高度每增加1000米,气温就降低6℃.如果现在地面的气温是27℃,那么8000米的高空的气温大约是多少?
课后作业
一、选择题
1.某市2020年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高(
).
A.-10℃
B.-6℃
C.6℃
D.10℃
2.若等式0□1=﹣1成立,则□内的运算符号为( )
A.
+
B.
﹣
C.
×
D.
÷
3.两个有理数相加,和小于其中一个加数而大于另一个加数,需满足
(
)
A.两个数都是正数
B.两个数都是负数
C.一个是正数,另一个是负数
D.至少有一个数是零
4.某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差
(
)
A.0.8kg
B.0.6kg
C.0.5kg
D.0.4kg
5.下列命题中,正确的是(
).
A.若a·b>0,则a>0,b>0
B.若a·b>0,则a<0,b<0
C.若a·b=0,则a=0且b=0
D.若a·b=0,则a=0或b=0
6.
下列说法错误的是
(
)
A.一个数与1相乘仍得这个数.
B.互为相反数(除0外)的两个数的商为-1.
C.一个数与-1相乘得这个数的相反数.
D.互为倒数的两个数的商为1.
7.
下列计算:①0-(-5)=-5;②;③;④;⑤若,则x的倒数是6.其中正确的个数是(
).
A.1
B.2
C.3
D.4
二、填空题
8.
计算:|﹣2|+2=________.(﹣6)×(﹣)= .
9.某月股票M开盘价20元,上午10点跌1.6元,下午收盘时又涨了0.4元,则股票这天的收盘价是_______.
10.若,则
0,
0,
0.
11.
若|a|=5,b=-2,且a÷b>0,则a+b=________.
如果6个不等于0的数相乘得积为负数,则在这6个乘数中,正的乘数有
个
13.在-2,3,4,-5这四个数中,任取两个数相乘所得积最大的是
,所得的商最小是
。
14.
是一个简单的数值运算程序,当输入-1时,则输出的数值____.
三、解答题
15.计算题
(1)
(2)
(3)(-0.125)×(-18)×(-8)×0×(-1)
(4)(-6)×45+(-6)×55
(5)
(6)
16.
某人用400元购买了8套儿童服装,准备以一定价格出售,如果以每套儿童服装55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,﹣3,+2,+1,﹣2,﹣1,0,﹣2.(单位:元)
(1)当他卖完这八套儿童服装后是盈利还是亏损?
(2)盈利(或亏损)了多少钱?
