2020年人教版数学八年级上册:12.2 三角形全等的判定培优训练卷 (Word版 含解析)
文档属性
| 名称 | 2020年人教版数学八年级上册:12.2 三角形全等的判定培优训练卷 (Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 350.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 19:09:59 | ||
图片预览



文档简介
2020年人教版八年级上册:12.2
三角形全等的判定培优训练卷
一.选择题
1.如图,在△ABC中,AB=AC,BD=CD,点E,F是AD上的任意两点.若BC=8,AD=6,则图中阴影部分的面积为( )
A.12
B.20
C.24
D.48
2.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
3.如图,在一个宽度为AB长的小巷内,一个梯子的长为a,梯子的底端位于AB上的点P,将该梯子的顶端放于巷子一侧墙上的点C处,点C到AB的距离BC为b,梯子的倾斜角∠BPC为45°;将该梯子的顶端放于另一侧墙上的点D处,点D到AB的距离AD为c,且此时梯子的倾斜角∠APD为75°,则AB的长等于( )
A.a
B.b
C.
D.c
4.如图,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:其中正确的结论有( )
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN;⑤△AFN≌△AEM.
A.2个
B.3个
C.4个
D.5个
5.如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为( )
A.45°
B.30°
C.22.5°
D.15°
6.在△ABC中,高AD和BE所在的直线交于点H,且BH=AC,则∠ABC等于( )
A.45°
B.120°
C.45°或135°
D.45°或120°
二.填空题
7.如图,在△ABC中,AC=BC,过点A,B分别作过点C的直线的垂线AE,BF.若AE=CF=3,BF=4.5,则EF=
.
8.如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连接AD、CD,若∠B=56°,则∠ADC的大小为
度.
9.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是
秒.
10.(多选)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为
cm/s.
A.;B.1;C.1.5;D.2.
三.解答题
11.如图,在四边形ABCD中,AD∥BC,点M为对角线AC上一点,连接BM,若AC=BC,∠AMB=∠BCD,求证:△ADC≌△CMB.
12.如图所示,O是线段AC、BD的交点,并且AC=BD,AB=CD.小明认为证明图中的△AOB和△DOC全等,他说连接BC或AD就可以了,请你用一种方法试一试看.
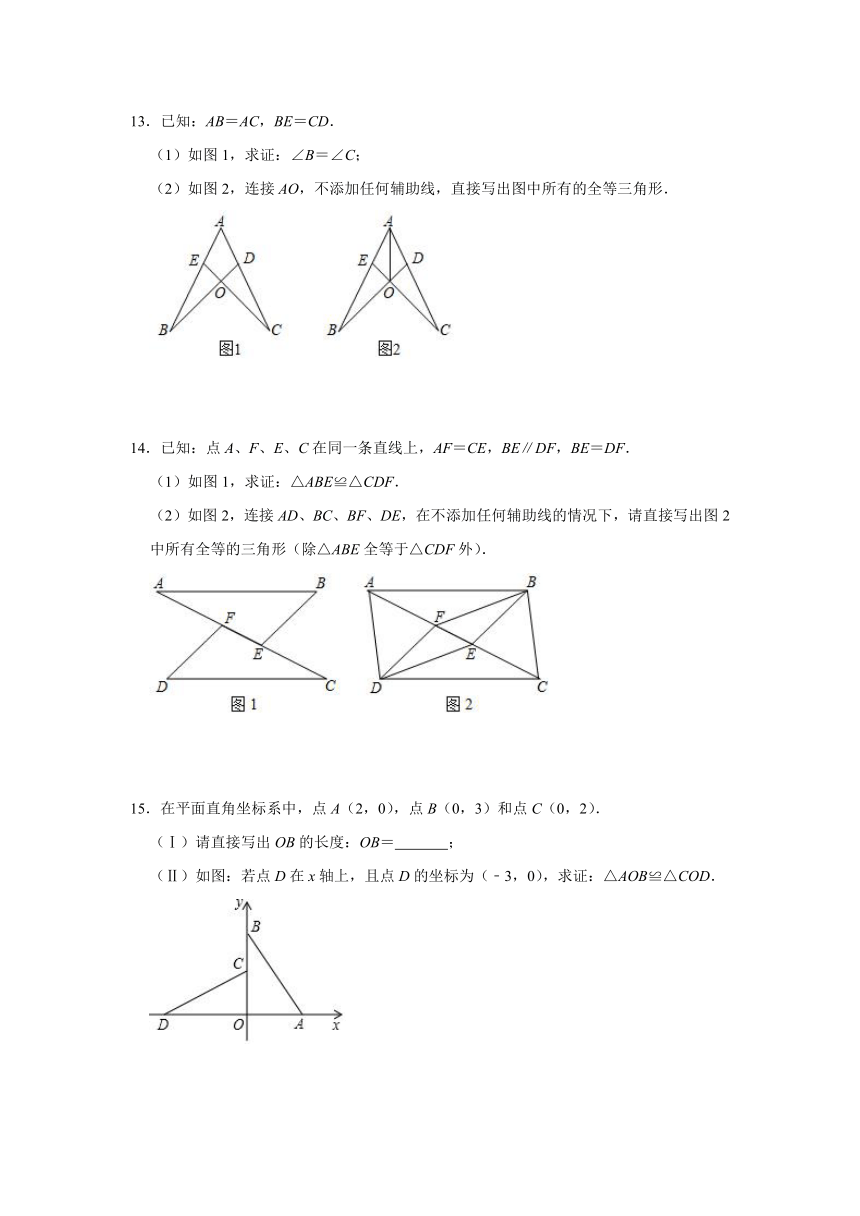
13.已知:AB=AC,BE=CD.
(1)如图1,求证:∠B=∠C;
(2)如图2,连接AO,不添加任何辅助线,直接写出图中所有的全等三角形.
14.已知:点A、F、E、C在同一条直线上,AF=CE,BE∥DF,BE=DF.
(1)如图1,求证:△ABE≌△CDF.
(2)如图2,连接AD、BC、BF、DE,在不添加任何辅助线的情况下,请直接写出图2中所有全等的三角形(除△ABE全等于△CDF外).
15.在平面直角坐标系中,点A(2,0),点B(0,3)和点C(0,2).
(Ⅰ)请直接写出OB的长度:OB=
;
(Ⅱ)如图:若点D在x轴上,且点D的坐标为(﹣3,0),求证:△AOB≌△COD.
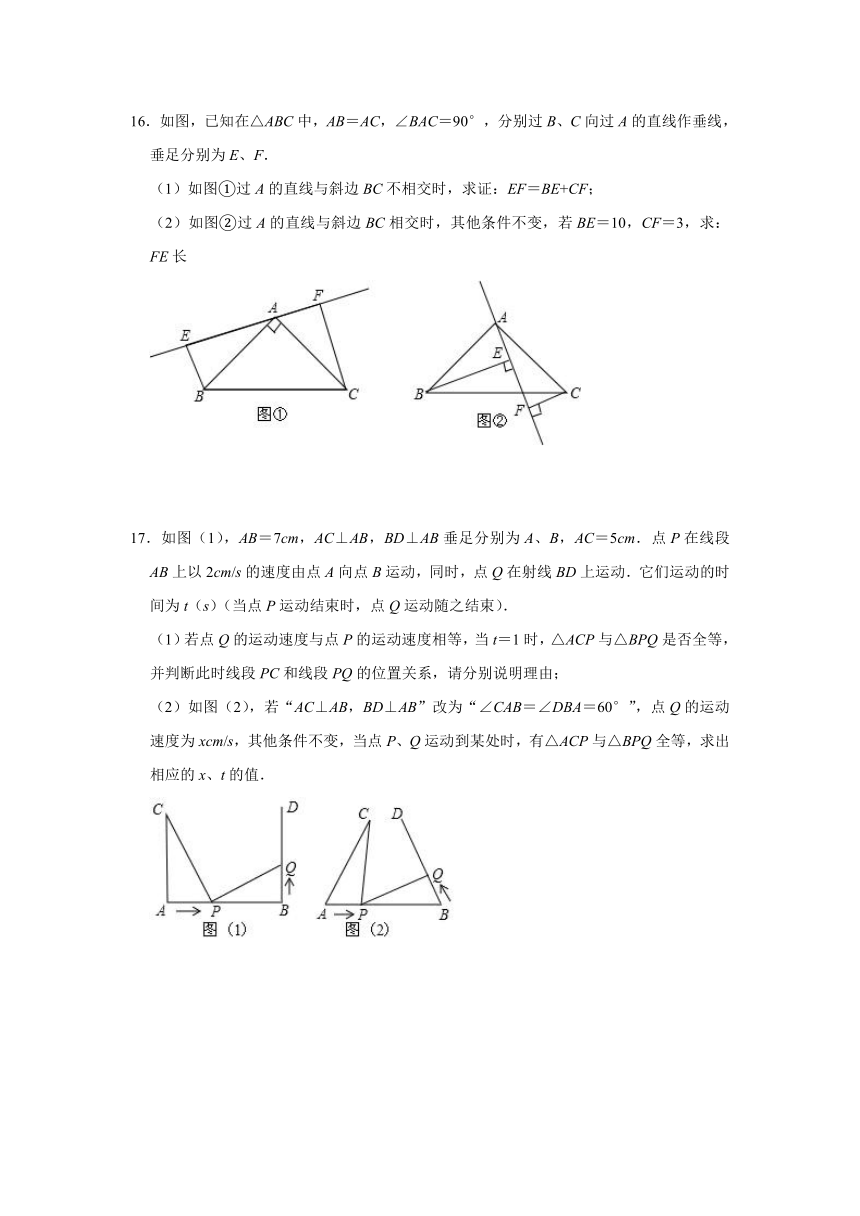
16.如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.
(1)如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;
(2)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE长
17.如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.
18.如图,在△ABC中,BC=8cm,AG∥BC,AG=8cm,点F从点B出发,沿线段BC以4cm/s的速度连续做往返运动,点E从点A出发沿线段AG以2cm/s的速度运动至点G,E、F两点同时出发,当点E到达点G时,E、F两点同时停止运动,EF与AC交于点D,设点E的运动时间为t(秒)
(1)分别写出当0<t<2和2<t<4时段BF的长度(用含t的代数式表示)
(2)当BF=AE时,求t的值;
(3)当△ADE≌△CDF时,直接写出所有满足条件的t值.
19.如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.
(1)用含t的式子表示PC的长为
;
(2)若点Q的运动速度与点P的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使三角形BPD与三角形CQP全等?
20.如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A点出发沿A﹣C路径向终点C运动;点Q从B点出发沿B﹣C﹣A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为多少时,△PEC与△QFC全等?
参考答案
一.选择题
1.解:∵AB=AC,BD=CD,AD=AD,
∴△ADC≌△ADB(SSS),
∴S△ADC=S△ADB,BD=BC,
∵BC=8,
∴BD=4,
∵S△BEF=S△CEF,AD=6,
∴S阴影=S△ADB=.
故选:A.
2.解:将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',
可得:CD=C'D',
A、下滑过程中,CC'与DD'不一定相等,说法错误;
B、下滑过程中,当△OCD与△OD'C'全等时,CC'=DD',说法错误;
C、若OC<OD,则下滑过程中,不存在某个位置使得CC'=DD',说法错误;
D、若OC>OD,则下滑过程中,当△OCD与△OD'C'全等时,一定存在某个位置使得CC'=DD',说法正确;
故选:D.
3.解:过点C作CE⊥AD于E,如图所示:
则四边形ABCE是矩形,
∴AB=CE,∠CED=∠DAP=90°,
∵∠BPC=45°,∠APD=75°,
∴∠CPD=180°﹣45°﹣75°=60°,
∵CP=DP=a,
∴△CPD是等边三角形,
∴CD=DP,∠PDC=60°,
∵∠ADP=90°﹣75°=15°,
∴∠EDC=15°+60°=75°,
∴∠EDC=∠APD,
在△EDC和△APD中,
,
∴△EDC≌△APD(AAS),
∴CE=AD,
∴AB=AD=c,
故选:D.
4.解:∵∠E=∠F=90°,∠B=∠C,AE=AF,
∴△ABE≌△ACF(AAS),
∴BE=CF,AF=AE,故②正确,
∠BAE=∠CAF,
∠BAE﹣∠BAC=∠CAF﹣∠BAC,
∴∠1=∠2,故①正确,
∵△ABE≌△ACF,
∴AB=AC,
又∠BAC=∠CAB,∠B=∠C
△ACN≌△ABM(ASA),故③正确,
CD=DN不能证明成立,故④错误
∵∠1=∠2,∠F=∠E,AF=AE,
∴△AFN≌△AEM(ASA),故⑤正确,
故选:C.
5.解:
连接AD,延长AC、DE交于M,
∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=∠DAC==22.5°,
故选:C.
6.解:分为三种情况:
①如图1,
∵AD、BE是△ABC的高,
∴∠ADC=∠BDH=90°,∠BEC=90°,
∴∠C+∠CAD=90°,∠C+∠HBD=90°,
∴∠CAD=∠HBD,
在△HBD和△CAD中
,
∴△HBD≌△CAD(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
②如图2,
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠HDB=∠AEH=90°,
∴∠H+∠HAE=∠C+∠HAE=90°,
∴∠H=∠C,
∵在△HBD和△CAD中,
,
∴△HBD≌△CAD(AAS),
∴AD=BD,
∴∠DAB=∠DBA,
∵∠ADB=90°,
∴∠ABD=45°,
∴∠ABC=180°﹣45°=135°;
③
∵高AD和BE所在的直线交于点H,
∴∠HDB=∠ADC=∠HEA=90°,
∴∠H+∠DAC=90°,∠H+∠HBD=90°,
∴∠DAC=∠HBD,
在△DAC和△DBH中
∴△DAC≌△DBH(AAS),
∴AD=BD,
∵∠ADB=90°,
∴∠ABC=∠CAB=45°,
故选:C.
二.填空题
7.解:∵过点A,B分别作过点C的直线的垂线AE,BF,
∴∠AEC=∠CFB=90°,
在Rt△AEC和Rt△CFB中,,
∴Rt△AEC≌Rt△CFB(HL),
∴EC=BF=4.5,
∴EF=EC+CF=4.5+3=7.5,
故答案为:7.5.
8.解:由作图可知:AD=BC,AB=CD,AC=CA,
∴△ABC≌△CDA(SSS),
∴∠ADC=∠B=56°,
故答案为:56.
9.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°,
∴∠CMA+∠C=90°,
∴∠C=∠DMB.
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴BD=AM=12米,
∴BM=20﹣12=8(米),
∵该人的运动速度为2m/s,
∴他到达点M时,运动时间为8÷2=4(s).
故答案为4.
10.解:当△ACP≌△BPQ时,
则AC=BP,AP=BQ,
∵AC=3cm,
∴BP=3cm,
∵AB=4cm,
∴AP=1cm,
∴BQ=1cm,
∴点Q的速度为:1÷(1÷1)=1(cm/s);
当△ACP≌△BQP时,
则AC=BQ,AP=BP,
∵AB=4cm,AC=BD=3cm,
∴AP=BP=2cm,BQ=3cm,
∴点Q的速度为:3÷(2÷1)=1.5(cm/s);
故选:B、C.
三.解答题
11.证明:∵AD∥BC,
∴∠DAC=∠MCB,
∵∠AMB=∠BCD,∠CBM+∠ACB=∠AMB,∠ACB+∠ACD=∠BCD,
∴∠CBM=∠ACD,
在△ADC和△CMB中,
,
∴△ADC≌△CMB(ASA).
12.证明:连接BC,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS),
∴∠A=∠D,
又在△AOB和△DOC中
,
∴△AOB≌△DOC(AAS).
13.证明:(1)∵AB=AC,BE=CD,
∴AB﹣BE=AC﹣CD,
即AE=AD,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠C;
(2)图中的全等三角形有△ABD≌△ACE,△AEO≌△ADO,△BEO≌△CDO,△ABO≌△ACO,
理由是:∵在△ABO和△ACO中,
,
∴△ABO≌△ACO(AAS);
由(1)知:△ABD≌△ACE;
∵在△AEO和△ADO中,
,
∴△AEO≌△ADO(SAS);
∵在△BEO和△CDO中,
,
∴△BEO≌△CDO(AAS).
14.(1)证明:∵AF=CE,
∴AF+EF=CE+EF,
即AE=CF,
∵BE∥DF,
∴∠AEB=∠CFD,
在△ABE和△CDF中
,
∴△ABE≌△CDF(SAS);
(2)图2中的全等三角形有△ABC≌△CDA,△AFB≌△CED,△ADE≌△CBF,△ADF≌△CBE,
理由是:∵△ABE≌△CDF,
∴AB=CD,∠BAC=∠DCA,
在△ABCHE△CDA中
,
∴△ABC≌△CDA(SAS),
∴AD=BC,∠DAC=∠BCA,
在△AFB和△CED中
,
∴△AFB≌△CED(SAS),
在△ADE和△CBF中
,
∴△ADE≌△CBF(SAS),
在△ADF和△CBE中
,
∴△ADF≌△CBE(SAS).
15.(I)解:∵点B(0,3),
∴OB=3,
故答案为:3;
(II)证明:∵点A(2,0),点B(0,3)和点C(0,2),点D的坐标为(﹣3,0),
∴OC=OA=2,OB=OD=3,
在△AOB和△COD中
∴△AOB≌△COD(SAS).
16.(1)证明:∵BE⊥EA,CF⊥AF,
∴∠BAC=∠BEA=∠CFE=90°,
∴∠EAB+∠CAF=90°,∠EBA+∠EAB=90°,
∴∠CAF=∠EBA,
在△ABE和△AFC中,
∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,
∴△BEA≌△AFC.
∴EA=FC,BE=AF.
∴EF=EB+CF.
(2)解:∵BE⊥EA,CF⊥AF,
∴∠BAC=∠BEA=∠CFE=90°,
∴∠EAB+∠CAF=90°,∠ABE+∠EAB=90°,
∴∠CAF=∠ABE,
在△ABE和△AFC中,
∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,
∴△BEA≌△AFC.
∴EA=FC=3,BE=AF=10.
∴EF=AF﹣CF=10﹣3=7.
17.解:(1)△ACP≌△BPQ,
∵AC⊥AB,BD⊥AB
∴∠A=∠B=90°
∵AP=BQ=2,
∴BP=5,
∴BP=AC,
在△ACP和△BPQ中,,
∴△ACP≌△BPQ;
∴∠C=∠BPQ,
∵∠C+∠APC=90°,
∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(2)存在x的值,使得△ACP与△BPQ全等,
①若△ACP≌△BPQ,
则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t
解得:x=,t=.
18.解:(1)当0<t≤2时,BF=4t,
当2<t≤4时,BF=16﹣4t;
(2)由题意得,16﹣4t=2t,
解得t=;
(3)当0<t≤2时,△ADE≌△CDF,
则AE=CF,即8﹣4t=2t,
解得t=,
当2<t≤4时,△ADE≌△CDF,
则AE=CF,即4t﹣8=2t,
解得t=4,
则t=或4时,△ADE≌△CDF.
19.解:(1)BP=2t,则PC=BC﹣BP=12﹣2t;
故答案为(12﹣2t)cm.
(2)当t=2时,BP=CQ=2×2=4厘米,
∵BD=8厘米.
又∵PC=BC﹣BP,BC=12厘米,
∴PC=12﹣4=8厘米,
∴PC=BD,
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,,
∴△BPD≌△CQP(SAS);
③∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,
∴BP=PC=6cm,CQ=BD=8cm,
∴点P,点Q运动的时间t===3秒,
∴VQ==厘米/秒.
即点Q的运动速度是厘米/秒时,能够使三角形BPD与三角形CQP全等.
20.解:设运动时间为t秒时,△PEC≌△QFC,
∵△PEC≌△QFC,
∴斜边CP=CQ,
有2种情况:①P在AC上,Q在BC上,
CP=6﹣t,CQ=8﹣3t,
∴6﹣t=8﹣3t,
∴t=1;
②P、Q都在AC上,此时P、Q重合,
∴CP=6﹣t=3t﹣8,
∴t=3.5;
答:点P运动1s或3.5s时,△PEC与△QFC全等.
三角形全等的判定培优训练卷
一.选择题
1.如图,在△ABC中,AB=AC,BD=CD,点E,F是AD上的任意两点.若BC=8,AD=6,则图中阴影部分的面积为( )
A.12
B.20
C.24
D.48
2.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是( )
A.下滑过程中,始终有CC'=DD'
B.下滑过程中,始终有CC'≠DD'
C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'
D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'
3.如图,在一个宽度为AB长的小巷内,一个梯子的长为a,梯子的底端位于AB上的点P,将该梯子的顶端放于巷子一侧墙上的点C处,点C到AB的距离BC为b,梯子的倾斜角∠BPC为45°;将该梯子的顶端放于另一侧墙上的点D处,点D到AB的距离AD为c,且此时梯子的倾斜角∠APD为75°,则AB的长等于( )
A.a
B.b
C.
D.c
4.如图,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:其中正确的结论有( )
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN;⑤△AFN≌△AEM.
A.2个
B.3个
C.4个
D.5个
5.如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为( )
A.45°
B.30°
C.22.5°
D.15°
6.在△ABC中,高AD和BE所在的直线交于点H,且BH=AC,则∠ABC等于( )
A.45°
B.120°
C.45°或135°
D.45°或120°
二.填空题
7.如图,在△ABC中,AC=BC,过点A,B分别作过点C的直线的垂线AE,BF.若AE=CF=3,BF=4.5,则EF=
.
8.如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连接AD、CD,若∠B=56°,则∠ADC的大小为
度.
9.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是
秒.
10.(多选)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为
cm/s.
A.;B.1;C.1.5;D.2.
三.解答题
11.如图,在四边形ABCD中,AD∥BC,点M为对角线AC上一点,连接BM,若AC=BC,∠AMB=∠BCD,求证:△ADC≌△CMB.
12.如图所示,O是线段AC、BD的交点,并且AC=BD,AB=CD.小明认为证明图中的△AOB和△DOC全等,他说连接BC或AD就可以了,请你用一种方法试一试看.
13.已知:AB=AC,BE=CD.
(1)如图1,求证:∠B=∠C;
(2)如图2,连接AO,不添加任何辅助线,直接写出图中所有的全等三角形.
14.已知:点A、F、E、C在同一条直线上,AF=CE,BE∥DF,BE=DF.
(1)如图1,求证:△ABE≌△CDF.
(2)如图2,连接AD、BC、BF、DE,在不添加任何辅助线的情况下,请直接写出图2中所有全等的三角形(除△ABE全等于△CDF外).
15.在平面直角坐标系中,点A(2,0),点B(0,3)和点C(0,2).
(Ⅰ)请直接写出OB的长度:OB=
;
(Ⅱ)如图:若点D在x轴上,且点D的坐标为(﹣3,0),求证:△AOB≌△COD.
16.如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.
(1)如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;
(2)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE长
17.如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.
18.如图,在△ABC中,BC=8cm,AG∥BC,AG=8cm,点F从点B出发,沿线段BC以4cm/s的速度连续做往返运动,点E从点A出发沿线段AG以2cm/s的速度运动至点G,E、F两点同时出发,当点E到达点G时,E、F两点同时停止运动,EF与AC交于点D,设点E的运动时间为t(秒)
(1)分别写出当0<t<2和2<t<4时段BF的长度(用含t的代数式表示)
(2)当BF=AE时,求t的值;
(3)当△ADE≌△CDF时,直接写出所有满足条件的t值.
19.如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.
(1)用含t的式子表示PC的长为
;
(2)若点Q的运动速度与点P的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使三角形BPD与三角形CQP全等?
20.如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A点出发沿A﹣C路径向终点C运动;点Q从B点出发沿B﹣C﹣A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为多少时,△PEC与△QFC全等?
参考答案
一.选择题
1.解:∵AB=AC,BD=CD,AD=AD,
∴△ADC≌△ADB(SSS),
∴S△ADC=S△ADB,BD=BC,
∵BC=8,
∴BD=4,
∵S△BEF=S△CEF,AD=6,
∴S阴影=S△ADB=.
故选:A.
2.解:将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',
可得:CD=C'D',
A、下滑过程中,CC'与DD'不一定相等,说法错误;
B、下滑过程中,当△OCD与△OD'C'全等时,CC'=DD',说法错误;
C、若OC<OD,则下滑过程中,不存在某个位置使得CC'=DD',说法错误;
D、若OC>OD,则下滑过程中,当△OCD与△OD'C'全等时,一定存在某个位置使得CC'=DD',说法正确;
故选:D.
3.解:过点C作CE⊥AD于E,如图所示:
则四边形ABCE是矩形,
∴AB=CE,∠CED=∠DAP=90°,
∵∠BPC=45°,∠APD=75°,
∴∠CPD=180°﹣45°﹣75°=60°,
∵CP=DP=a,
∴△CPD是等边三角形,
∴CD=DP,∠PDC=60°,
∵∠ADP=90°﹣75°=15°,
∴∠EDC=15°+60°=75°,
∴∠EDC=∠APD,
在△EDC和△APD中,
,
∴△EDC≌△APD(AAS),
∴CE=AD,
∴AB=AD=c,
故选:D.
4.解:∵∠E=∠F=90°,∠B=∠C,AE=AF,
∴△ABE≌△ACF(AAS),
∴BE=CF,AF=AE,故②正确,
∠BAE=∠CAF,
∠BAE﹣∠BAC=∠CAF﹣∠BAC,
∴∠1=∠2,故①正确,
∵△ABE≌△ACF,
∴AB=AC,
又∠BAC=∠CAB,∠B=∠C
△ACN≌△ABM(ASA),故③正确,
CD=DN不能证明成立,故④错误
∵∠1=∠2,∠F=∠E,AF=AE,
∴△AFN≌△AEM(ASA),故⑤正确,
故选:C.
5.解:
连接AD,延长AC、DE交于M,
∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=∠DAC==22.5°,
故选:C.
6.解:分为三种情况:
①如图1,
∵AD、BE是△ABC的高,
∴∠ADC=∠BDH=90°,∠BEC=90°,
∴∠C+∠CAD=90°,∠C+∠HBD=90°,
∴∠CAD=∠HBD,
在△HBD和△CAD中
,
∴△HBD≌△CAD(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
②如图2,
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠HDB=∠AEH=90°,
∴∠H+∠HAE=∠C+∠HAE=90°,
∴∠H=∠C,
∵在△HBD和△CAD中,
,
∴△HBD≌△CAD(AAS),
∴AD=BD,
∴∠DAB=∠DBA,
∵∠ADB=90°,
∴∠ABD=45°,
∴∠ABC=180°﹣45°=135°;
③
∵高AD和BE所在的直线交于点H,
∴∠HDB=∠ADC=∠HEA=90°,
∴∠H+∠DAC=90°,∠H+∠HBD=90°,
∴∠DAC=∠HBD,
在△DAC和△DBH中
∴△DAC≌△DBH(AAS),
∴AD=BD,
∵∠ADB=90°,
∴∠ABC=∠CAB=45°,
故选:C.
二.填空题
7.解:∵过点A,B分别作过点C的直线的垂线AE,BF,
∴∠AEC=∠CFB=90°,
在Rt△AEC和Rt△CFB中,,
∴Rt△AEC≌Rt△CFB(HL),
∴EC=BF=4.5,
∴EF=EC+CF=4.5+3=7.5,
故答案为:7.5.
8.解:由作图可知:AD=BC,AB=CD,AC=CA,
∴△ABC≌△CDA(SSS),
∴∠ADC=∠B=56°,
故答案为:56.
9.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°,
∴∠CMA+∠C=90°,
∴∠C=∠DMB.
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴BD=AM=12米,
∴BM=20﹣12=8(米),
∵该人的运动速度为2m/s,
∴他到达点M时,运动时间为8÷2=4(s).
故答案为4.
10.解:当△ACP≌△BPQ时,
则AC=BP,AP=BQ,
∵AC=3cm,
∴BP=3cm,
∵AB=4cm,
∴AP=1cm,
∴BQ=1cm,
∴点Q的速度为:1÷(1÷1)=1(cm/s);
当△ACP≌△BQP时,
则AC=BQ,AP=BP,
∵AB=4cm,AC=BD=3cm,
∴AP=BP=2cm,BQ=3cm,
∴点Q的速度为:3÷(2÷1)=1.5(cm/s);
故选:B、C.
三.解答题
11.证明:∵AD∥BC,
∴∠DAC=∠MCB,
∵∠AMB=∠BCD,∠CBM+∠ACB=∠AMB,∠ACB+∠ACD=∠BCD,
∴∠CBM=∠ACD,
在△ADC和△CMB中,
,
∴△ADC≌△CMB(ASA).
12.证明:连接BC,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS),
∴∠A=∠D,
又在△AOB和△DOC中
,
∴△AOB≌△DOC(AAS).
13.证明:(1)∵AB=AC,BE=CD,
∴AB﹣BE=AC﹣CD,
即AE=AD,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠C;
(2)图中的全等三角形有△ABD≌△ACE,△AEO≌△ADO,△BEO≌△CDO,△ABO≌△ACO,
理由是:∵在△ABO和△ACO中,
,
∴△ABO≌△ACO(AAS);
由(1)知:△ABD≌△ACE;
∵在△AEO和△ADO中,
,
∴△AEO≌△ADO(SAS);
∵在△BEO和△CDO中,
,
∴△BEO≌△CDO(AAS).
14.(1)证明:∵AF=CE,
∴AF+EF=CE+EF,
即AE=CF,
∵BE∥DF,
∴∠AEB=∠CFD,
在△ABE和△CDF中
,
∴△ABE≌△CDF(SAS);
(2)图2中的全等三角形有△ABC≌△CDA,△AFB≌△CED,△ADE≌△CBF,△ADF≌△CBE,
理由是:∵△ABE≌△CDF,
∴AB=CD,∠BAC=∠DCA,
在△ABCHE△CDA中
,
∴△ABC≌△CDA(SAS),
∴AD=BC,∠DAC=∠BCA,
在△AFB和△CED中
,
∴△AFB≌△CED(SAS),
在△ADE和△CBF中
,
∴△ADE≌△CBF(SAS),
在△ADF和△CBE中
,
∴△ADF≌△CBE(SAS).
15.(I)解:∵点B(0,3),
∴OB=3,
故答案为:3;
(II)证明:∵点A(2,0),点B(0,3)和点C(0,2),点D的坐标为(﹣3,0),
∴OC=OA=2,OB=OD=3,
在△AOB和△COD中
∴△AOB≌△COD(SAS).
16.(1)证明:∵BE⊥EA,CF⊥AF,
∴∠BAC=∠BEA=∠CFE=90°,
∴∠EAB+∠CAF=90°,∠EBA+∠EAB=90°,
∴∠CAF=∠EBA,
在△ABE和△AFC中,
∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,
∴△BEA≌△AFC.
∴EA=FC,BE=AF.
∴EF=EB+CF.
(2)解:∵BE⊥EA,CF⊥AF,
∴∠BAC=∠BEA=∠CFE=90°,
∴∠EAB+∠CAF=90°,∠ABE+∠EAB=90°,
∴∠CAF=∠ABE,
在△ABE和△AFC中,
∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,
∴△BEA≌△AFC.
∴EA=FC=3,BE=AF=10.
∴EF=AF﹣CF=10﹣3=7.
17.解:(1)△ACP≌△BPQ,
∵AC⊥AB,BD⊥AB
∴∠A=∠B=90°
∵AP=BQ=2,
∴BP=5,
∴BP=AC,
在△ACP和△BPQ中,,
∴△ACP≌△BPQ;
∴∠C=∠BPQ,
∵∠C+∠APC=90°,
∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(2)存在x的值,使得△ACP与△BPQ全等,
①若△ACP≌△BPQ,
则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t
解得:x=,t=.
18.解:(1)当0<t≤2时,BF=4t,
当2<t≤4时,BF=16﹣4t;
(2)由题意得,16﹣4t=2t,
解得t=;
(3)当0<t≤2时,△ADE≌△CDF,
则AE=CF,即8﹣4t=2t,
解得t=,
当2<t≤4时,△ADE≌△CDF,
则AE=CF,即4t﹣8=2t,
解得t=4,
则t=或4时,△ADE≌△CDF.
19.解:(1)BP=2t,则PC=BC﹣BP=12﹣2t;
故答案为(12﹣2t)cm.
(2)当t=2时,BP=CQ=2×2=4厘米,
∵BD=8厘米.
又∵PC=BC﹣BP,BC=12厘米,
∴PC=12﹣4=8厘米,
∴PC=BD,
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,,
∴△BPD≌△CQP(SAS);
③∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,
∴BP=PC=6cm,CQ=BD=8cm,
∴点P,点Q运动的时间t===3秒,
∴VQ==厘米/秒.
即点Q的运动速度是厘米/秒时,能够使三角形BPD与三角形CQP全等.
20.解:设运动时间为t秒时,△PEC≌△QFC,
∵△PEC≌△QFC,
∴斜边CP=CQ,
有2种情况:①P在AC上,Q在BC上,
CP=6﹣t,CQ=8﹣3t,
∴6﹣t=8﹣3t,
∴t=1;
②P、Q都在AC上,此时P、Q重合,
∴CP=6﹣t=3t﹣8,
∴t=3.5;
答:点P运动1s或3.5s时,△PEC与△QFC全等.
