2020-2021学年新教材北师大版必修第一册 8 数学建模活动(一) 练测评(word含答案解析)
文档属性
| 名称 | 2020-2021学年新教材北师大版必修第一册 8 数学建模活动(一) 练测评(word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 296.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 19:20:17 | ||
图片预览



文档简介
第八章 数学建模活动(一)
§1 走近数学建模
§2 数学建模的主要步骤
§3 数学建模活动的主要过程
必备知识基础练 进阶训练第一层
知识点一 建立数学模型
1.生物学家认为,睡眠中的恒温动物依然会消耗体内能量,主要是为了保持体温.研究表明,消耗的能量E与通过心脏的血液量Q成正比;并且根据生物学常识知道,动物的体重与体积成正比.血流量Q是单位时间流过的血量,脉博率f是单位时间心跳的次数;还有一些生物学假设,例如,心脏每次收缩挤压出来的血量q与心脏大小成正比,动物心脏的大小与这个动物体积的大小成正比.
下表给出一些动物体重与脉搏率对应的数据.
动物名 体重/g 脉搏率/(心跳次数·min-1)
鼠 25 670
大鼠 200 420
豚鼠 300 300
兔 2 000 205
小狗 5 000 120
大狗 30 000 85
羊 50 000 70
马 450 000 38
建立一个数学模型将通过心脏的血流量与体重联系起来,进一步建立脉搏率与体重的关系,讨论你模型中的假设,并用上表中的数据检验模型.
知识点二 数学建模的主要步骤
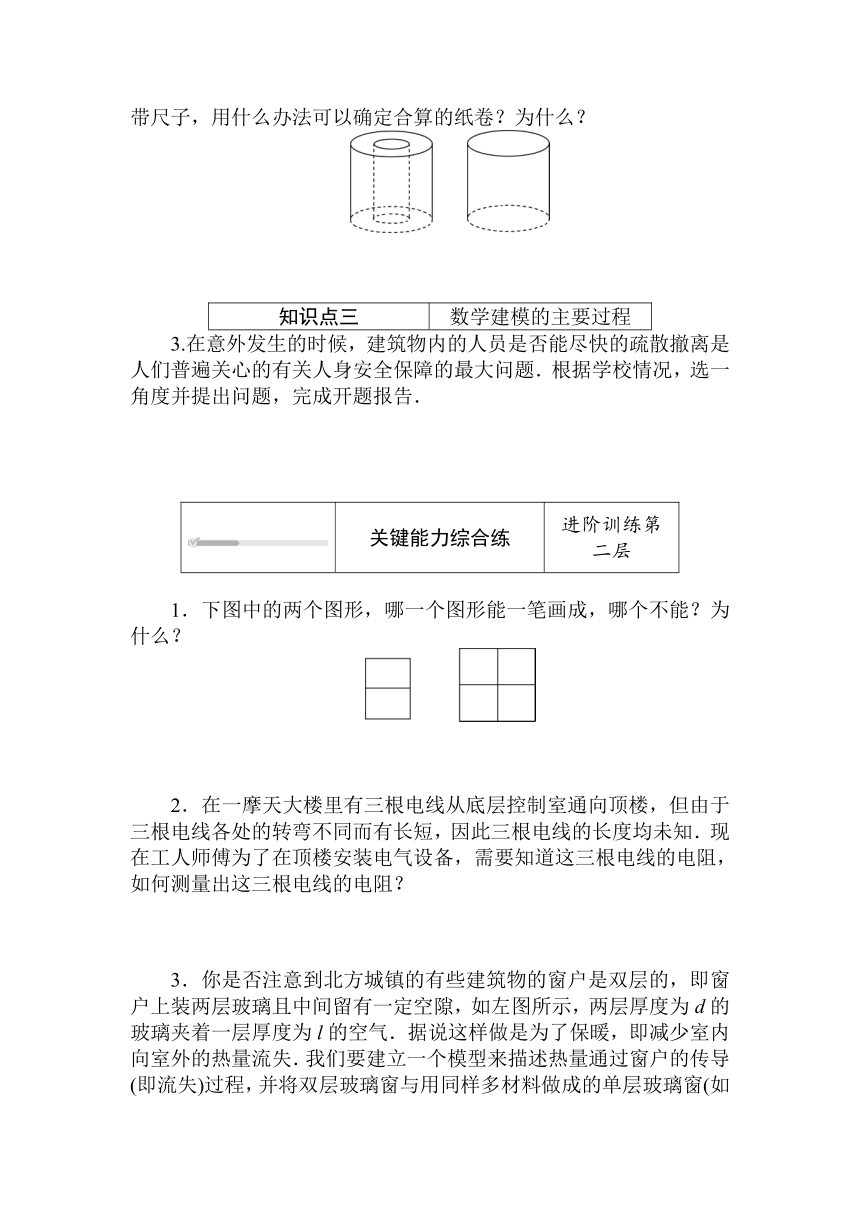
2.超市卖某一品牌的卫生纸,这种卫生纸分“有芯”和“无芯”两种纸卷,如图,两种纸具有同样的材质和厚度,纸卷的高度和单价也一样,若预购买这种卫生纸,但不知道哪种纸卷更合算,如果没有带尺子,用什么办法可以确定合算的纸卷?为什么?
知识点三 数学建模的主要过程
3.在意外发生的时候,建筑物内的人员是否能尽快的疏散撤离是人们普遍关心的有关人身安全保障的最大问题.根据学校情况,选一角度并提出问题,完成开题报告.
关键能力综合练 进阶训练第二层
1.下图中的两个图形,哪一个图形能一笔画成,哪个不能?为什么?
2.在一摩天大楼里有三根电线从底层控制室通向顶楼,但由于三根电线各处的转弯不同而有长短,因此三根电线的长度均未知.现在工人师傅为了在顶楼安装电气设备,需要知道这三根电线的电阻,如何测量出这三根电线的电阻?
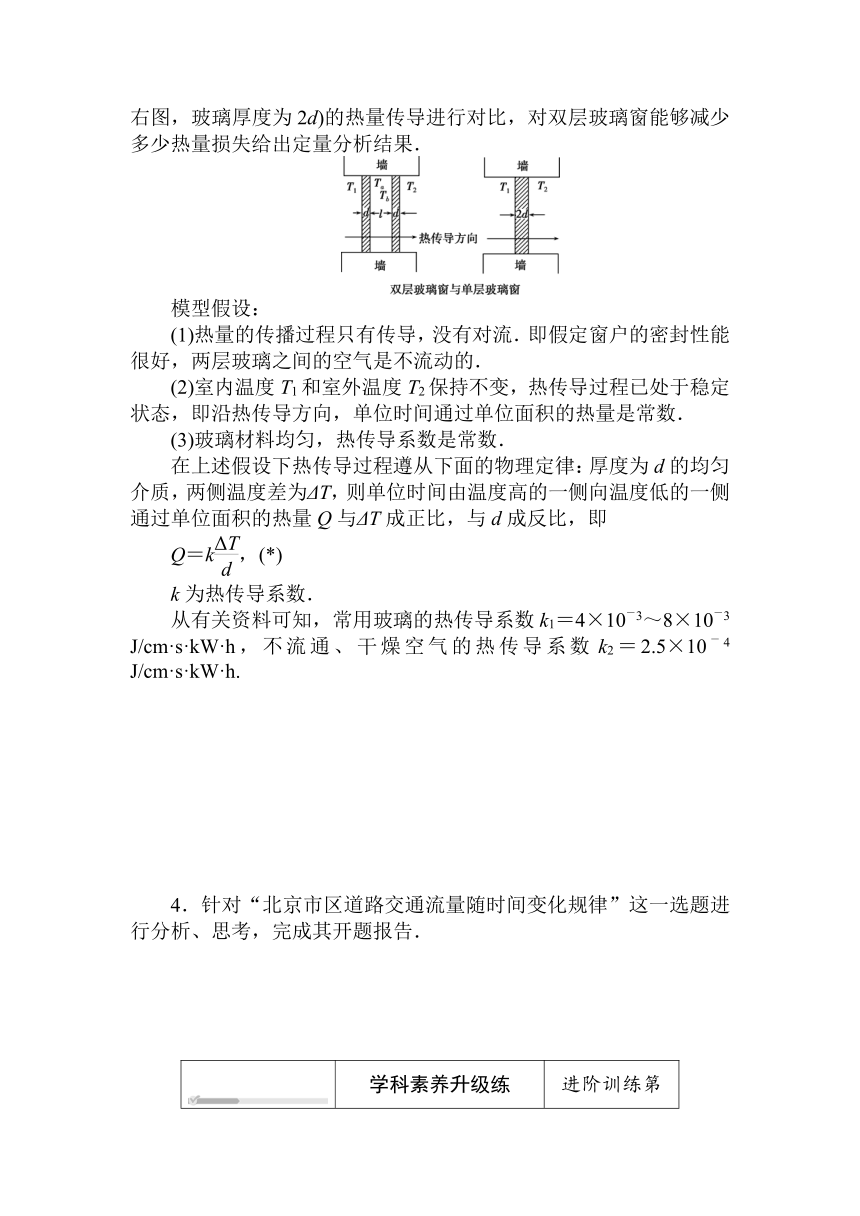
3.你是否注意到北方城镇的有些建筑物的窗户是双层的,即窗户上装两层玻璃且中间留有一定空隙,如左图所示,两层厚度为d的玻璃夹着一层厚度为l的空气.据说这样做是为了保暖,即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的传导(即流失)过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗(如右图,玻璃厚度为2d)的热量传导进行对比,对双层玻璃窗能够减少多少热量损失给出定量分析结果.
模型假设:
(1)热量的传播过程只有传导,没有对流.即假定窗户的密封性能很好,两层玻璃之间的空气是不流动的.
(2)室内温度T1和室外温度T2保持不变,热传导过程已处于稳定状态,即沿热传导方向,单位时间通过单位面积的热量是常数.
(3)玻璃材料均匀,热传导系数是常数.
在上述假设下热传导过程遵从下面的物理定律:厚度为d的均匀介质,两侧温度差为ΔT,则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量Q与ΔT成正比,与d成反比,即
Q=k,(*)
k为热传导系数.
从有关资料可知,常用玻璃的热传导系数k1=4×10-3~8×10-3 J/cm·s·kW·h,不流通、干燥空气的热传导系数k2=2.5×10-4 J/cm·s·kW·h.
4.针对“北京市区道路交通流量随时间变化规律”这一选题进行分析、思考,完成其开题报告.
学科素养升级练 进阶训练第三层
1.在商场中,我们经常可以看到同一种商品会有多种大小不同的型号,其价格也各不相同.对比型号和价格,我们很容易发现:当商品的“量”增加时,价格也会增加;但是价格的增加与“量”的增加是不成比例的,也就是说你买的商品的“量”越多,商品的平均价格越低,有人认为这是商家的营销策略,买得越多越划算,这样顾客往往倾向于购买大包装的商品.大包装的商品真的是薄利多销吗?
就这一问题通过调查、分析、研究,完成选题,开题报告.
第八章 数学建模活动(一)
§1 走近数学建模
§2 数学建模的主要步骤
§3 数学建模活动的主要过程
必备知识基础练
1.解析:建模过程如下:
(1)因为动物体温通过身体表面散发热量,表面积越大,散发的热量越多,保持体温需要的能量也就越大,所以动物体内消耗的能量E与身体的表面积S成正比,可以表示为E=p1S.又因为动物体内消耗的能量E与通过心脏的血流量Q成正比,可以表示为E=p2Q.因此得到Q=pS,其中p1,p2和p均为正的比例系数.
另一方面,因为体积V与体重W成正比,可以表示为V=r1W;又因为表面积S大约与体积V的次方成正比,可以表示为S=r2V,因此得到S=rW,其中r1,r2,r为正的比例系数.所以可以构建血流量与体重关系的数学模型Q=k1W,其中k1为正的比例系数.
(2)根据脉搏率的定义f=,再根据生物学假设q=cW(c为正的比例系数),最后得到f==,也就是f=kW-,其中k为正的待定系数.
脉搏率与体重关系的数学模型说明,恒温动物体重越大,脉搏率越低;脉搏率与体重的次方成反比,表中的数据基本上反映了这个反比例的关系.右图是以ln W和ln f为坐标的散点图.可以看出,数据取对数之后基本满足线性关系,因此得到体重和脉搏率的对数线性模型,可以把这个模型表达为ln f=ln k-.
2.解析:
合算就是纸的量多,因为纸卷的高度和单价一样,我们只要比较两种纸卷截面的面积,取较大的就合算,为此可以各取一个纸卷,令无芯纸卷截面的圆心压在有芯纸卷截面的芯(即小圆)上,如右图,然后看无芯纸卷截面上与有芯纸卷截面的芯相切的直径端点,若端点在有芯纸卷截面的大圆上,则两种纸卷的量相等;若在其内则买有芯纸卷合算;若在其外则买无芯纸卷合算.
证明:设有芯纸卷截面的内、外半径分别为r,R,大圆内与小圆相切的弦长为d,无芯纸卷截面的直径为D,于是,2=R2-r2,
当D=d时,S有芯=π(R2-r2)=π2=π2=S无芯,
当D>d时,S有芯=π(R2-r2)=π2<π2=S无芯.
当D<d时,S有芯=π(R2-r2)=π2>π2=S无芯.
3.解析:
要解决的问题 在教学楼一楼有一排四间教室,学生可以沿教室外走廊一直走到尽头的出口,试分析学生撤离所用时间
选题的原因及意义 建立数学模型给出最佳撤离方案,同时就教学楼设计给出合理化建议
建模问题的可行性分析 教师可在教学楼内组织学生进行多次演习,只需测量几个简单的参数.
基本模型、解决问题的大体思路和步骤 做出合理假设,列出有关的参数.队列中人与人之间的距离将为常数,记为d,队列行进的速度也是常数v,令第i个教室中的人数为ni+1人,第i个教室的门口到前一个教室的门口的距离为Li,教室门的宽度为D.疏散时教室内第一个人到达教室门口所用的时间忽略不计.
T1,2=
预期结果和结果呈现方式 建立一个来描述建筑物内人员疏散的最合适的模型,一份有求解过程的文字报告
参考文献 《数学模型与数学建模》 北京师范大学数学科学学院
其他说明
关键能力综合练
1.解析:(1)标点:标出双数点和单数点.
(2)判断:第一个只有两个单数点,所以可以一笔画,第二个有4个单数点,所以不能一笔画,
2.解析:不妨用a,b,c及a′,b′,c′分别表示三根电线的底端和顶端,并用aa′,bb′,cc′分别表示三根电线,假设x,y,z分别是aa′,bb′,cc′的电阻,这是三个未知数,电表不能直接测量出这三个未知数.然而我们可以把a′和b′连接起来,在a和b处测量得电阻x+y为l;然后将b′和c′连接起来,在b和c处测量得y+z为m,连接a′和c′可测得x+z为n,这样得三元一次方程组
由三元一次线性方程组解出x,y,z即得三根电线的电阻.
3.解析:记双层窗内层玻璃的外侧温度是Ta,外层玻璃的内侧温度是Tb,如图,玻璃的热传导系数为k1,空气的热传导系数为k2,由(*)式单位时间单位面积的热量传导(即热量流失)为
Q1=k1=k2=k1,
消去Ta,Tb,可得Q1=,s=h,h=,
对于厚度为2d的单层玻璃窗,容易写出其热量传导为
Q2=k1.
二者之比为=,
显然Q1<Q2.为了得到更具体的结果,我们需要k1和k2的数据.16≤≤32.
在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时,我们作最保守的估计,即取=16,可得=,h=,
比值反映了双层玻璃窗在减少热量损失上的功效,它只与h=有关,我们给出-h的曲线,当h增加时,迅速下降,而当h超过一定值(比如h>4)后下降变缓,可见h不必选择过大.
4.解析:
要解决的问题 随着北京城市的不断发展,交通成了饱受关注的话题,那么北京市区主要道路交通流量随时间变化有什么样的规律?
选题的原 因及意义 为市民日常出行乃至相关部门的政策制定提供参考
建模问题的 可行性分析 时间和车流量满足一定的函数关系
基本模型、解 决问题的大体
思路和步骤 观测某主干道每3分钟内通过的车流量,进行分析比较,时刻为自变量x(单位:小时),车流量为因变量y(单位:辆/3分钟)
预期结果和结 果呈现方式 一个能够反映时间与车流量的函数模型,一份有求解过程的文字报告
成员和分工 全组共同制定研究计划商讨确定数学模型
同学甲(组长,侧重组织讨论,把握工作方向)
同学乙、丙(侧重信息采集、数据计算整理)
同学丁(侧重讨论记录、报告撰写、结果复核)
参考文献 《北京交通状况的分析与预测》
百度地图http://map.baidu.com
其他说明
学科素养升级练
1.解析:
要解决的 问题 到商场买牙膏,从划算的角度讲,同一品牌的牙膏我们是买小包装的好,还是大包装的好呢?
解决问题 的方法 同一品牌的牙膏形状是相似的,通过比例建立价格与质量的函数关系
相关问题 分析及其
假设 我们设商品的价格为y(元),质量为x(g),看能否找出y与x的函数关系式:y=f(x).为了方便叙述,我们引入“∝”这一符号,当y与x成比例,即y=kx(k为常数)时,记作y∝x
建模求解的 主要过程 设商品的成本为P(元),一般来说,商品价格=商品成本×(1+利润率),所以有y∝P.而商品的成本主要分为生产成本和包装成本两部分,分别设为P1和P2,即有y∝(P1+P2).商品的生产成本P1与商品的质量x成比例,即P1∝x;而商品的包装成本P2与商品的表面积S成比例,即P2∝S,而S∝V,V∝x(这里V指商品的体积),故有P2∝x.从而我们可以假设y=ax+bx.
下面我们用实际数据来检验这一函数表达式的准确性,因为在函数中有两个待定系数,所以我们只需要代入两组(x,y)值即可求出a,b的值.
将(65,14)和(90,17.6)代入y=ax+bx中,可得
解得a≈0.0225,b≈0.7756,所以y=0.0225x+0.7756x
结果检验 将x=120代入,得y=21.57,与实际价格21.60元相差0.03;再将x=180代入,得y=28.77,与实际价格28.30元相差0.47元.因此,我们推导出来的函数表达式还是比较准确的.
这一步得到单位质量价格y′=0.0225+0.7756x-,由几何画板做出y′-x的关系图为
可以看出随牙膏质量的增加,单位质量价格的减小量在减少,因此不能盲目的认为越大的包装越便宜
小组成员 和分工 全组共同制定研究计划商讨确定数学模型
同学甲(组长,侧重组织讨论,把握工作方向)
同学乙、丙(侧重信息采集、数据计算整理)
同学丁(侧重讨论记录、报告撰写、结果复核)
反思与 拓展 在以上推导过程中,我们只考虑了生产和包装两种主要的成本,如果将运输成本、超市上架费、网站仓储费等因素也考虑进去,可能结果会更准确,但是模型也会复杂很多,可操作性就差了.另外,商品包装的材质也会对价格造成较大的影响,比如同一品牌的巧克力,可能会有普通包装、精品包装和礼品包装三种,这时如果只考虑分量对价格的影响,显然是不合适的
研究的收 获和感受,
得到的帮
助和致谢 对自己确定相关因素和“寻找”数据有了切身感受.分工合作使我们理解了未来的学习和工作模式,学会了向别人学习,同时积极表达自己的思考.感谢我们的数学老师和家长提供的参考意见和对我们的鼓励
参考文献 《中学数学建模与探究》张思明
其他说明
§1 走近数学建模
§2 数学建模的主要步骤
§3 数学建模活动的主要过程
必备知识基础练 进阶训练第一层
知识点一 建立数学模型
1.生物学家认为,睡眠中的恒温动物依然会消耗体内能量,主要是为了保持体温.研究表明,消耗的能量E与通过心脏的血液量Q成正比;并且根据生物学常识知道,动物的体重与体积成正比.血流量Q是单位时间流过的血量,脉博率f是单位时间心跳的次数;还有一些生物学假设,例如,心脏每次收缩挤压出来的血量q与心脏大小成正比,动物心脏的大小与这个动物体积的大小成正比.
下表给出一些动物体重与脉搏率对应的数据.
动物名 体重/g 脉搏率/(心跳次数·min-1)
鼠 25 670
大鼠 200 420
豚鼠 300 300
兔 2 000 205
小狗 5 000 120
大狗 30 000 85
羊 50 000 70
马 450 000 38
建立一个数学模型将通过心脏的血流量与体重联系起来,进一步建立脉搏率与体重的关系,讨论你模型中的假设,并用上表中的数据检验模型.
知识点二 数学建模的主要步骤
2.超市卖某一品牌的卫生纸,这种卫生纸分“有芯”和“无芯”两种纸卷,如图,两种纸具有同样的材质和厚度,纸卷的高度和单价也一样,若预购买这种卫生纸,但不知道哪种纸卷更合算,如果没有带尺子,用什么办法可以确定合算的纸卷?为什么?
知识点三 数学建模的主要过程
3.在意外发生的时候,建筑物内的人员是否能尽快的疏散撤离是人们普遍关心的有关人身安全保障的最大问题.根据学校情况,选一角度并提出问题,完成开题报告.
关键能力综合练 进阶训练第二层
1.下图中的两个图形,哪一个图形能一笔画成,哪个不能?为什么?
2.在一摩天大楼里有三根电线从底层控制室通向顶楼,但由于三根电线各处的转弯不同而有长短,因此三根电线的长度均未知.现在工人师傅为了在顶楼安装电气设备,需要知道这三根电线的电阻,如何测量出这三根电线的电阻?
3.你是否注意到北方城镇的有些建筑物的窗户是双层的,即窗户上装两层玻璃且中间留有一定空隙,如左图所示,两层厚度为d的玻璃夹着一层厚度为l的空气.据说这样做是为了保暖,即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的传导(即流失)过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗(如右图,玻璃厚度为2d)的热量传导进行对比,对双层玻璃窗能够减少多少热量损失给出定量分析结果.
模型假设:
(1)热量的传播过程只有传导,没有对流.即假定窗户的密封性能很好,两层玻璃之间的空气是不流动的.
(2)室内温度T1和室外温度T2保持不变,热传导过程已处于稳定状态,即沿热传导方向,单位时间通过单位面积的热量是常数.
(3)玻璃材料均匀,热传导系数是常数.
在上述假设下热传导过程遵从下面的物理定律:厚度为d的均匀介质,两侧温度差为ΔT,则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量Q与ΔT成正比,与d成反比,即
Q=k,(*)
k为热传导系数.
从有关资料可知,常用玻璃的热传导系数k1=4×10-3~8×10-3 J/cm·s·kW·h,不流通、干燥空气的热传导系数k2=2.5×10-4 J/cm·s·kW·h.
4.针对“北京市区道路交通流量随时间变化规律”这一选题进行分析、思考,完成其开题报告.
学科素养升级练 进阶训练第三层
1.在商场中,我们经常可以看到同一种商品会有多种大小不同的型号,其价格也各不相同.对比型号和价格,我们很容易发现:当商品的“量”增加时,价格也会增加;但是价格的增加与“量”的增加是不成比例的,也就是说你买的商品的“量”越多,商品的平均价格越低,有人认为这是商家的营销策略,买得越多越划算,这样顾客往往倾向于购买大包装的商品.大包装的商品真的是薄利多销吗?
就这一问题通过调查、分析、研究,完成选题,开题报告.
第八章 数学建模活动(一)
§1 走近数学建模
§2 数学建模的主要步骤
§3 数学建模活动的主要过程
必备知识基础练
1.解析:建模过程如下:
(1)因为动物体温通过身体表面散发热量,表面积越大,散发的热量越多,保持体温需要的能量也就越大,所以动物体内消耗的能量E与身体的表面积S成正比,可以表示为E=p1S.又因为动物体内消耗的能量E与通过心脏的血流量Q成正比,可以表示为E=p2Q.因此得到Q=pS,其中p1,p2和p均为正的比例系数.
另一方面,因为体积V与体重W成正比,可以表示为V=r1W;又因为表面积S大约与体积V的次方成正比,可以表示为S=r2V,因此得到S=rW,其中r1,r2,r为正的比例系数.所以可以构建血流量与体重关系的数学模型Q=k1W,其中k1为正的比例系数.
(2)根据脉搏率的定义f=,再根据生物学假设q=cW(c为正的比例系数),最后得到f==,也就是f=kW-,其中k为正的待定系数.
脉搏率与体重关系的数学模型说明,恒温动物体重越大,脉搏率越低;脉搏率与体重的次方成反比,表中的数据基本上反映了这个反比例的关系.右图是以ln W和ln f为坐标的散点图.可以看出,数据取对数之后基本满足线性关系,因此得到体重和脉搏率的对数线性模型,可以把这个模型表达为ln f=ln k-.
2.解析:
合算就是纸的量多,因为纸卷的高度和单价一样,我们只要比较两种纸卷截面的面积,取较大的就合算,为此可以各取一个纸卷,令无芯纸卷截面的圆心压在有芯纸卷截面的芯(即小圆)上,如右图,然后看无芯纸卷截面上与有芯纸卷截面的芯相切的直径端点,若端点在有芯纸卷截面的大圆上,则两种纸卷的量相等;若在其内则买有芯纸卷合算;若在其外则买无芯纸卷合算.
证明:设有芯纸卷截面的内、外半径分别为r,R,大圆内与小圆相切的弦长为d,无芯纸卷截面的直径为D,于是,2=R2-r2,
当D=d时,S有芯=π(R2-r2)=π2=π2=S无芯,
当D>d时,S有芯=π(R2-r2)=π2<π2=S无芯.
当D<d时,S有芯=π(R2-r2)=π2>π2=S无芯.
3.解析:
要解决的问题 在教学楼一楼有一排四间教室,学生可以沿教室外走廊一直走到尽头的出口,试分析学生撤离所用时间
选题的原因及意义 建立数学模型给出最佳撤离方案,同时就教学楼设计给出合理化建议
建模问题的可行性分析 教师可在教学楼内组织学生进行多次演习,只需测量几个简单的参数.
基本模型、解决问题的大体思路和步骤 做出合理假设,列出有关的参数.队列中人与人之间的距离将为常数,记为d,队列行进的速度也是常数v,令第i个教室中的人数为ni+1人,第i个教室的门口到前一个教室的门口的距离为Li,教室门的宽度为D.疏散时教室内第一个人到达教室门口所用的时间忽略不计.
T1,2=
预期结果和结果呈现方式 建立一个来描述建筑物内人员疏散的最合适的模型,一份有求解过程的文字报告
参考文献 《数学模型与数学建模》 北京师范大学数学科学学院
其他说明
关键能力综合练
1.解析:(1)标点:标出双数点和单数点.
(2)判断:第一个只有两个单数点,所以可以一笔画,第二个有4个单数点,所以不能一笔画,
2.解析:不妨用a,b,c及a′,b′,c′分别表示三根电线的底端和顶端,并用aa′,bb′,cc′分别表示三根电线,假设x,y,z分别是aa′,bb′,cc′的电阻,这是三个未知数,电表不能直接测量出这三个未知数.然而我们可以把a′和b′连接起来,在a和b处测量得电阻x+y为l;然后将b′和c′连接起来,在b和c处测量得y+z为m,连接a′和c′可测得x+z为n,这样得三元一次方程组
由三元一次线性方程组解出x,y,z即得三根电线的电阻.
3.解析:记双层窗内层玻璃的外侧温度是Ta,外层玻璃的内侧温度是Tb,如图,玻璃的热传导系数为k1,空气的热传导系数为k2,由(*)式单位时间单位面积的热量传导(即热量流失)为
Q1=k1=k2=k1,
消去Ta,Tb,可得Q1=,s=h,h=,
对于厚度为2d的单层玻璃窗,容易写出其热量传导为
Q2=k1.
二者之比为=,
显然Q1<Q2.为了得到更具体的结果,我们需要k1和k2的数据.16≤≤32.
在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时,我们作最保守的估计,即取=16,可得=,h=,
比值反映了双层玻璃窗在减少热量损失上的功效,它只与h=有关,我们给出-h的曲线,当h增加时,迅速下降,而当h超过一定值(比如h>4)后下降变缓,可见h不必选择过大.
4.解析:
要解决的问题 随着北京城市的不断发展,交通成了饱受关注的话题,那么北京市区主要道路交通流量随时间变化有什么样的规律?
选题的原 因及意义 为市民日常出行乃至相关部门的政策制定提供参考
建模问题的 可行性分析 时间和车流量满足一定的函数关系
基本模型、解 决问题的大体
思路和步骤 观测某主干道每3分钟内通过的车流量,进行分析比较,时刻为自变量x(单位:小时),车流量为因变量y(单位:辆/3分钟)
预期结果和结 果呈现方式 一个能够反映时间与车流量的函数模型,一份有求解过程的文字报告
成员和分工 全组共同制定研究计划商讨确定数学模型
同学甲(组长,侧重组织讨论,把握工作方向)
同学乙、丙(侧重信息采集、数据计算整理)
同学丁(侧重讨论记录、报告撰写、结果复核)
参考文献 《北京交通状况的分析与预测》
百度地图http://map.baidu.com
其他说明
学科素养升级练
1.解析:
要解决的 问题 到商场买牙膏,从划算的角度讲,同一品牌的牙膏我们是买小包装的好,还是大包装的好呢?
解决问题 的方法 同一品牌的牙膏形状是相似的,通过比例建立价格与质量的函数关系
相关问题 分析及其
假设 我们设商品的价格为y(元),质量为x(g),看能否找出y与x的函数关系式:y=f(x).为了方便叙述,我们引入“∝”这一符号,当y与x成比例,即y=kx(k为常数)时,记作y∝x
建模求解的 主要过程 设商品的成本为P(元),一般来说,商品价格=商品成本×(1+利润率),所以有y∝P.而商品的成本主要分为生产成本和包装成本两部分,分别设为P1和P2,即有y∝(P1+P2).商品的生产成本P1与商品的质量x成比例,即P1∝x;而商品的包装成本P2与商品的表面积S成比例,即P2∝S,而S∝V,V∝x(这里V指商品的体积),故有P2∝x.从而我们可以假设y=ax+bx.
下面我们用实际数据来检验这一函数表达式的准确性,因为在函数中有两个待定系数,所以我们只需要代入两组(x,y)值即可求出a,b的值.
将(65,14)和(90,17.6)代入y=ax+bx中,可得
解得a≈0.0225,b≈0.7756,所以y=0.0225x+0.7756x
结果检验 将x=120代入,得y=21.57,与实际价格21.60元相差0.03;再将x=180代入,得y=28.77,与实际价格28.30元相差0.47元.因此,我们推导出来的函数表达式还是比较准确的.
这一步得到单位质量价格y′=0.0225+0.7756x-,由几何画板做出y′-x的关系图为
可以看出随牙膏质量的增加,单位质量价格的减小量在减少,因此不能盲目的认为越大的包装越便宜
小组成员 和分工 全组共同制定研究计划商讨确定数学模型
同学甲(组长,侧重组织讨论,把握工作方向)
同学乙、丙(侧重信息采集、数据计算整理)
同学丁(侧重讨论记录、报告撰写、结果复核)
反思与 拓展 在以上推导过程中,我们只考虑了生产和包装两种主要的成本,如果将运输成本、超市上架费、网站仓储费等因素也考虑进去,可能结果会更准确,但是模型也会复杂很多,可操作性就差了.另外,商品包装的材质也会对价格造成较大的影响,比如同一品牌的巧克力,可能会有普通包装、精品包装和礼品包装三种,这时如果只考虑分量对价格的影响,显然是不合适的
研究的收 获和感受,
得到的帮
助和致谢 对自己确定相关因素和“寻找”数据有了切身感受.分工合作使我们理解了未来的学习和工作模式,学会了向别人学习,同时积极表达自己的思考.感谢我们的数学老师和家长提供的参考意见和对我们的鼓励
参考文献 《中学数学建模与探究》张思明
其他说明
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
