人教版八年级上册数学 12.1 全等三角形同步课件(26张)
文档属性
| 名称 | 人教版八年级上册数学 12.1 全等三角形同步课件(26张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-19 21:36:09 | ||
图片预览




文档简介
全等三角形
?
第十二章
12.1 全等三角形
课堂导练
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
了解全等形及全等三角形的有关概念,理解全等三角形的性质.
课前学案
1.__________________的两个图形叫做全等形.
2.________________的两个三角形叫做全等三角形.
3.把两个全等三角形重合到一起,重合的顶点叫做
__________,重合的边叫做__________,重合的
角叫做__________.
4.全等三角形的对应边_______,对应角_______.
相等
能够完全重合
能够完全重合
对应顶点
对应边
对应角
相等
课堂导练
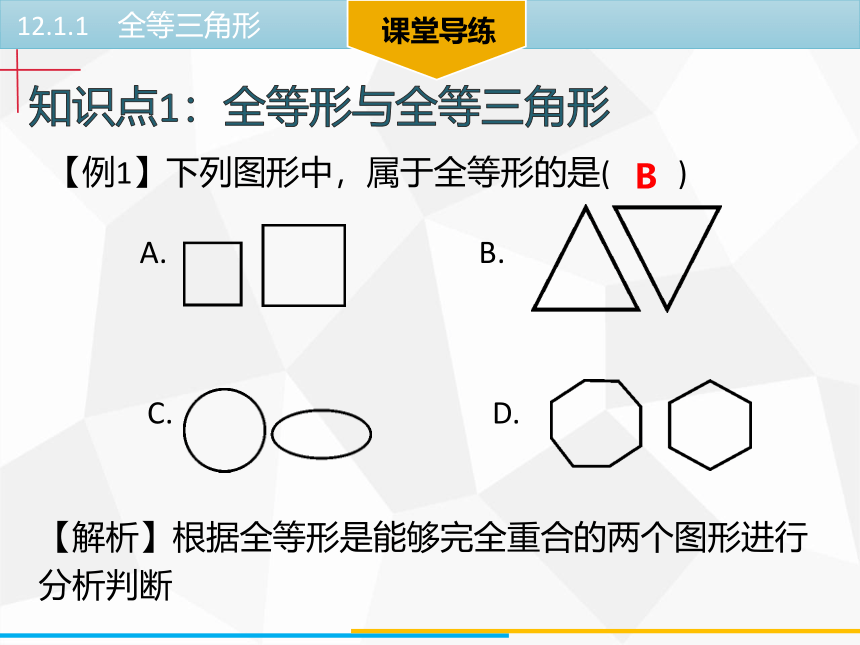
【例1】下列图形中,属于全等形的是( )
A. B.
C. D.
【解析】根据全等形是能够完全重合的两个图形进行分析判断
B
课堂导练
【答案】B
【点拔】全等形的识别方法:能够完全重合的两个图形是全等形.两个全等形的形状、大小完全相同.
课堂导练
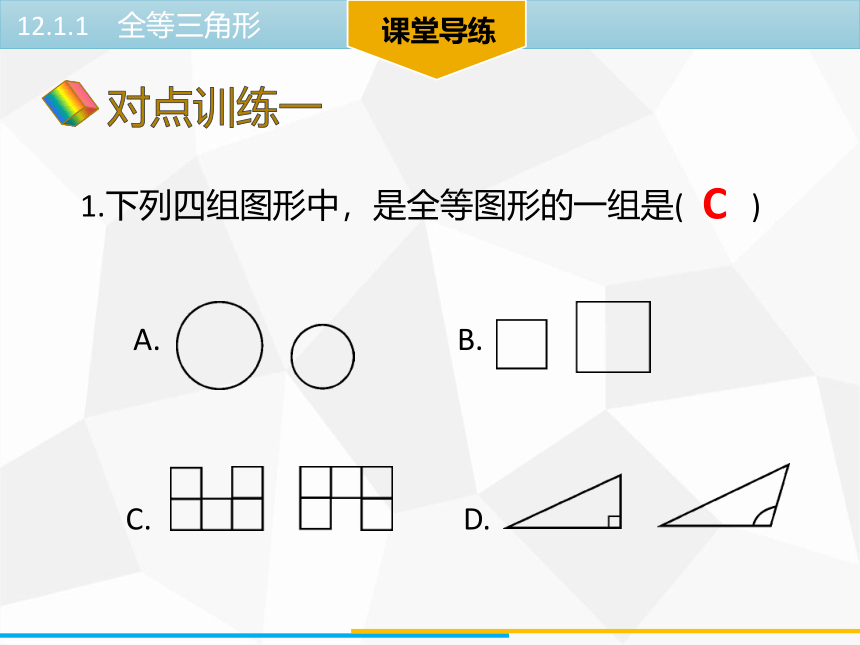
1.下列四组图形中,是全等图形的一组是( )
A. B.
C. D.
C
课堂导练
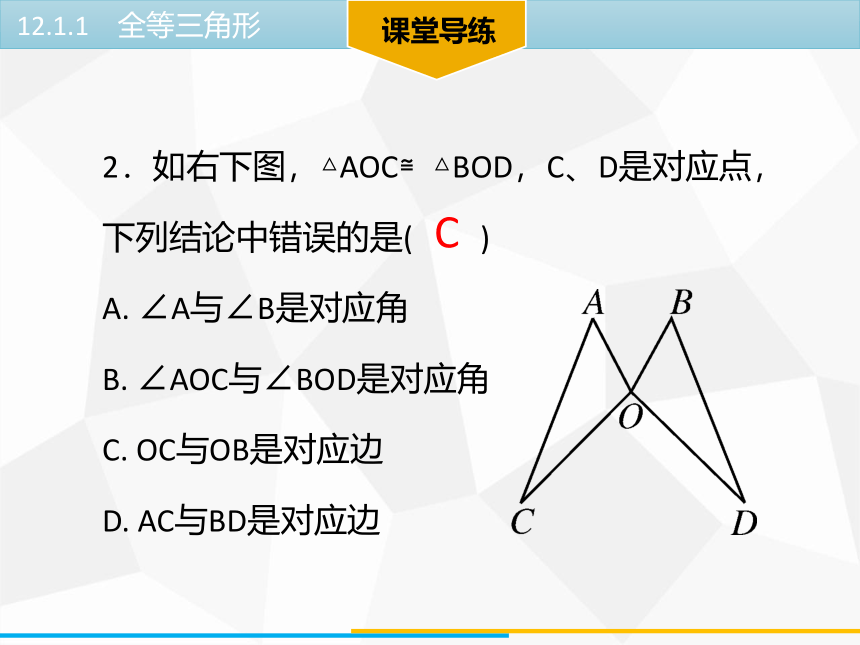
2.如右下图,△AOC≌△BOD,C、D是对应点,下列结论中错误的是( )
A. ∠A与∠B是对应角
B. ∠AOC与∠BOD是对应角
C. OC与OB是对应边
D. AC与BD是对应边
C
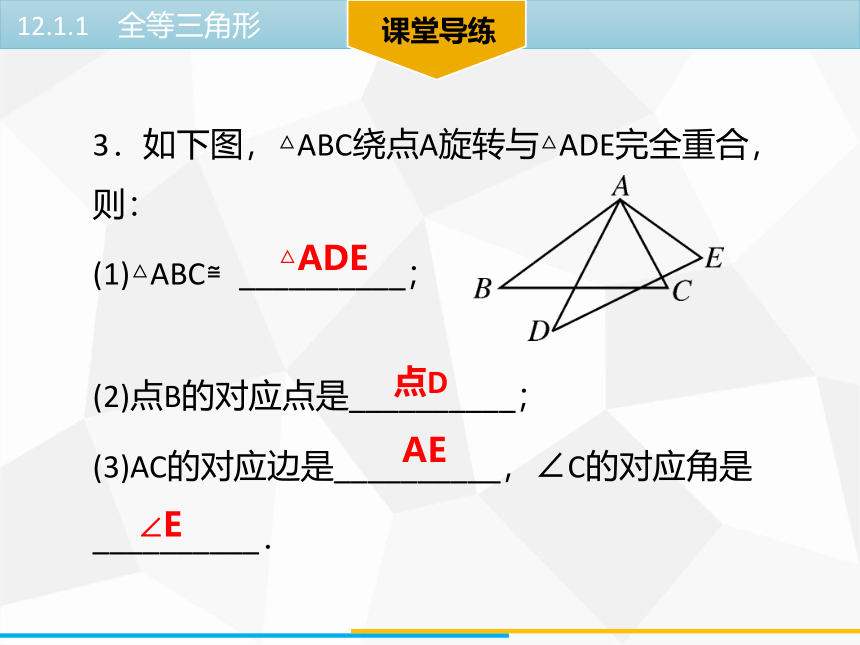
(2)点B的对应点是__________;
(3)AC的对应边是__________,∠C的对应角是__________.
课堂导练
3.如下图,△ABC绕点A旋转与△ADE完全重合,则:
(1)△ABC≌__________;
△ADE
点D
AE
∠E
课堂导练
【例2】如下图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【解析】根据全等三角形对应边相等,全等三角形对应角相等结合图形解答即可.
C
课堂导练
【答案】C
【点拔】本题考查了全等三角形的性质,熟记性质并准确识图,准确确定出对应边和对应角是解题的关键.
4.如下图,△AOC≌△BOD,C与D是对应点,那么下列结论中错误的是( )
A. ∠A=∠B
B. ∠AOC=∠BOD
C. AC=BD
D. AO=DO
课堂导练
D
5.如上图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠OAD=( )
A.95°
B.85°
C.75°
D.65°
课堂导练
B
6.如右下图,△ABC≌△BAD,如果AB=6cm,BD=5cm,AD=4cm,那么BC= ( )
A.4cm
B.5cm
C.6cm
D.无法确定
课堂导练
A
课后练案
7.下列图形中与左边的图形全等的是( )
B
课后练案
8.下列说法不正确的是( )
A.两个三角形全等,形状一定相同
B.两个三角形全等,面积一定相等
C.一个图形经过平移、旋转、翻折后,前后两个图形一定全等
D.所有的正方形都全等
D
课后练案
9.如下图,△ABC≌△DFE,下列说法中错误的是( )
A.∠A与∠D是对应角
D.AB与DF是对应边
C.∠ACB与∠DEF是对应角
D.BE与FC是对应边
D
课后练案
10.已知:如上图,△ABC≌△DEC,∠BCE=30°,则∠ACD的度数为( )
A.20°
B.30°
C.35°
D.40°
B
课后练案
11.如下图,D、E为△ABC两边AB、AC上的点,且DE∥BC,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=55°,则∠BDF等于( )
A.55°
B.60°
C.70°
D.90°
C
课后练案
12.如上图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则BE的长是( )
A.1
B.2
C.4
D.6
B
课后练案
13.如下图,点A、F、C、D在同一条直线上,且△ABC≌△DEF,求证:
(1)BC∥FE;
(2)AF=DC.
∵△ABC≌△DEF,
∴∠ACB=∠DFE,
∴BC∥FE.
∵△ABC≌△DEF,∴AC=DF,
∴AC-CF=DF-CF,∴AF=DC.
能力培优
14.如下图,△BAD≌△ACE,A、D、E三点在同一直线上.
(1)求证:BD=DE+CE;
∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∵AE=AD+DE,∴BD=DE+CE.
能力培优
(2)△ABD满足什么条件时,BD∥CE.
当△ABD是直角三角形且∠ADB=90°时,BD∥CE,∵△BAD≌△ACE,
∴∠AEC=∠BDA=90°,∵∠ADB=90°,∴∠BDE=90°,∴∠BDE=∠AEC,
∴BD∥CE.
能力培优
15.如下图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.
∵△ABC≌△ADE,∴∠ABC=∠ADE=25°,∴∠CAB=180°-∠ACB-∠ABC=50°,
∴∠DAB=∠CAD+∠CAB=60°,∴∠DFB=∠DAB+∠ABC=85°又∵△ABC≌△ADE,
∴∠DAE=∠BAC=50°,∴∠GAB=110°,
∴∠AGB=180°-∠GAB-∠ABC=45°.
能力培优
感谢聆听
?
第十二章
12.1 全等三角形
课堂导练
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
了解全等形及全等三角形的有关概念,理解全等三角形的性质.
课前学案
1.__________________的两个图形叫做全等形.
2.________________的两个三角形叫做全等三角形.
3.把两个全等三角形重合到一起,重合的顶点叫做
__________,重合的边叫做__________,重合的
角叫做__________.
4.全等三角形的对应边_______,对应角_______.
相等
能够完全重合
能够完全重合
对应顶点
对应边
对应角
相等
课堂导练
【例1】下列图形中,属于全等形的是( )
A. B.
C. D.
【解析】根据全等形是能够完全重合的两个图形进行分析判断
B
课堂导练
【答案】B
【点拔】全等形的识别方法:能够完全重合的两个图形是全等形.两个全等形的形状、大小完全相同.
课堂导练
1.下列四组图形中,是全等图形的一组是( )
A. B.
C. D.
C
课堂导练
2.如右下图,△AOC≌△BOD,C、D是对应点,下列结论中错误的是( )
A. ∠A与∠B是对应角
B. ∠AOC与∠BOD是对应角
C. OC与OB是对应边
D. AC与BD是对应边
C
(2)点B的对应点是__________;
(3)AC的对应边是__________,∠C的对应角是__________.
课堂导练
3.如下图,△ABC绕点A旋转与△ADE完全重合,则:
(1)△ABC≌__________;
△ADE
点D
AE
∠E
课堂导练
【例2】如下图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【解析】根据全等三角形对应边相等,全等三角形对应角相等结合图形解答即可.
C
课堂导练
【答案】C
【点拔】本题考查了全等三角形的性质,熟记性质并准确识图,准确确定出对应边和对应角是解题的关键.
4.如下图,△AOC≌△BOD,C与D是对应点,那么下列结论中错误的是( )
A. ∠A=∠B
B. ∠AOC=∠BOD
C. AC=BD
D. AO=DO
课堂导练
D
5.如上图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠OAD=( )
A.95°
B.85°
C.75°
D.65°
课堂导练
B
6.如右下图,△ABC≌△BAD,如果AB=6cm,BD=5cm,AD=4cm,那么BC= ( )
A.4cm
B.5cm
C.6cm
D.无法确定
课堂导练
A
课后练案
7.下列图形中与左边的图形全等的是( )
B
课后练案
8.下列说法不正确的是( )
A.两个三角形全等,形状一定相同
B.两个三角形全等,面积一定相等
C.一个图形经过平移、旋转、翻折后,前后两个图形一定全等
D.所有的正方形都全等
D
课后练案
9.如下图,△ABC≌△DFE,下列说法中错误的是( )
A.∠A与∠D是对应角
D.AB与DF是对应边
C.∠ACB与∠DEF是对应角
D.BE与FC是对应边
D
课后练案
10.已知:如上图,△ABC≌△DEC,∠BCE=30°,则∠ACD的度数为( )
A.20°
B.30°
C.35°
D.40°
B
课后练案
11.如下图,D、E为△ABC两边AB、AC上的点,且DE∥BC,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=55°,则∠BDF等于( )
A.55°
B.60°
C.70°
D.90°
C
课后练案
12.如上图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则BE的长是( )
A.1
B.2
C.4
D.6
B
课后练案
13.如下图,点A、F、C、D在同一条直线上,且△ABC≌△DEF,求证:
(1)BC∥FE;
(2)AF=DC.
∵△ABC≌△DEF,
∴∠ACB=∠DFE,
∴BC∥FE.
∵△ABC≌△DEF,∴AC=DF,
∴AC-CF=DF-CF,∴AF=DC.
能力培优
14.如下图,△BAD≌△ACE,A、D、E三点在同一直线上.
(1)求证:BD=DE+CE;
∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∵AE=AD+DE,∴BD=DE+CE.
能力培优
(2)△ABD满足什么条件时,BD∥CE.
当△ABD是直角三角形且∠ADB=90°时,BD∥CE,∵△BAD≌△ACE,
∴∠AEC=∠BDA=90°,∵∠ADB=90°,∴∠BDE=90°,∴∠BDE=∠AEC,
∴BD∥CE.
能力培优
15.如下图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.
∵△ABC≌△ADE,∴∠ABC=∠ADE=25°,∴∠CAB=180°-∠ACB-∠ABC=50°,
∴∠DAB=∠CAD+∠CAB=60°,∴∠DFB=∠DAB+∠ABC=85°又∵△ABC≌△ADE,
∴∠DAE=∠BAC=50°,∴∠GAB=110°,
∴∠AGB=180°-∠GAB-∠ABC=45°.
能力培优
感谢聆听
