西师大版小学数学六年级上册单元导学案-二、圆
文档属性
| 名称 | 西师大版小学数学六年级上册单元导学案-二、圆 |

|
|
| 格式 | doc | ||
| 文件大小 | 271.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 07:20:18 | ||
图片预览




文档简介
二、圆
《圆的认识(一)》导学案
【学习目标】
1.掌握画圆的方法,能借助圆规等工具画圆。
2.认识圆,知道圆的各部分名称。
3.掌握圆的特征,理解和掌握在同一个圆里半径和直径的关系。
【设问导读】
仔细阅读课本第12页的例1、例2,同时完成设问导读内容。
1.结合例1中的实物图指出圆在哪里,并说说生活中还有哪些地方有圆。
2.你想到画圆的方法有( )。
用你喜欢的方法在下面画一个圆。
3.画圆时可以用( ),用( )的一只脚( )在( ),另一只脚绕着这个点( )1圈,就画出了一个( )。
4.我们以前学过的平面图形有( ),它们都是由( )围成的;圆是由( )围成的。
5. 画圆时,固定的点是( ),一般用字母( )表示,圆心到圆上任意一点的线段是( ),一般用字母( )表示,通过圆心并且两端都在圆上的线段是( ),一般用字母( )表示。请在你画的圆里标记出圆心、半径和直径。
6.任意画一个圆,剪下来对折几次,量一量、比一比、说一说你发现了什么?
在同一个圆里,半径有( )条,长度都( );在同一个圆里,直径有( )条,长度都( )。
在同一个圆里,直径的长度是半径的( ),半径的长度是直径的( ),用字母表示为( )或( )。
圆是( )图形,每条直径所在的直线都是圆的( ),圆有( )条对称轴。
【自学检测】
用圆规画圆。
画几个圆心在同一点而半径不相等的圆; 画几个圆心不在同一点而半径相等的圆。
2.填表
圆一 圆二 圆三 圆四 圆五
r(m) 3 0.8
2.5
d(m)
6.4 3.6
【巩固练习】
1.判断
(1)圆有无数条对称轴。( )
(2)两端都在圆上的线段,就是直径。( )
(3)在一个圆内所有线段中,直径最长。( )
(4)两条半径相连就是直径。( )
(5)半径为5厘米的圆比直径为6厘米的圆小。( )
2.填空
(1)( )确定圆的位置,( )确定圆的大小,钟表的分针尖端转动一周形成的图形是( ),半径是( )的长度。
(2)在同一个圆里可以画( )直径,( )半径,圆内最长的线段是( )。
(3)在同一个圆中,如果半径是5厘米,那么直径则是( )厘米;如果直径是9厘米,则半径是( )厘米。
(4)画一个直径6厘米的圆,圆规两脚间的距离是( )厘米。
【拓展练习】 画一个半圆,并画出它的对称轴。
《圆的认识(二)》导学案
【学习目标】
1.认识圆心角、弧、扇形,理解并掌握它们的意义。
2.了解扇形的大小与它的圆心角的关系。
3.能用圆设计一些简单的图案。
【温故互查】
请同学们以二人小组完成下列内容(要求:第一题组员给组长讲,第二题组长给组员讲,互相补充纠正)。
1.画圆时,固定的点是( ),它决定圆的( );( )到圆上任意一点的线段是( ),它决定圆的( );通过( )并且两端都在( )的线段是( )。
2.圆有( )条半径,( )条直径;圆是( )图形,它有( )条对称轴;在同一个圆里,所有半径的长度都( ),所有直径的长度都( );在同一个圆里,( )的长度是( )的2倍,( )的长度是( )的一半。
【设问导读】
仔细阅读课本13页-14页的例3、例4,同时完成设问导读内容。
1.( )在圆心的角叫做圆心角;圆上两点之间的部分叫做( );由圆心角的( )和圆心角所对的( )围成的图形是扇形。
2.扇形是( )图形,扇形有( )条对称轴。
3.在同一个圆中,扇形的大小与这个扇形的( )的大小有关;在不同的圆中,扇形的大小与( )和( )有关。
4.想一想:例4中的这些图案中有哪些几何图形?是怎样画出来的?
5.“在正方形中,设计用线段绕成圆的图案”中,正方形的每边是怎样等分的?每边的数是怎样排列的?每条线段连接的顺序又是怎样的?
【自学检测】
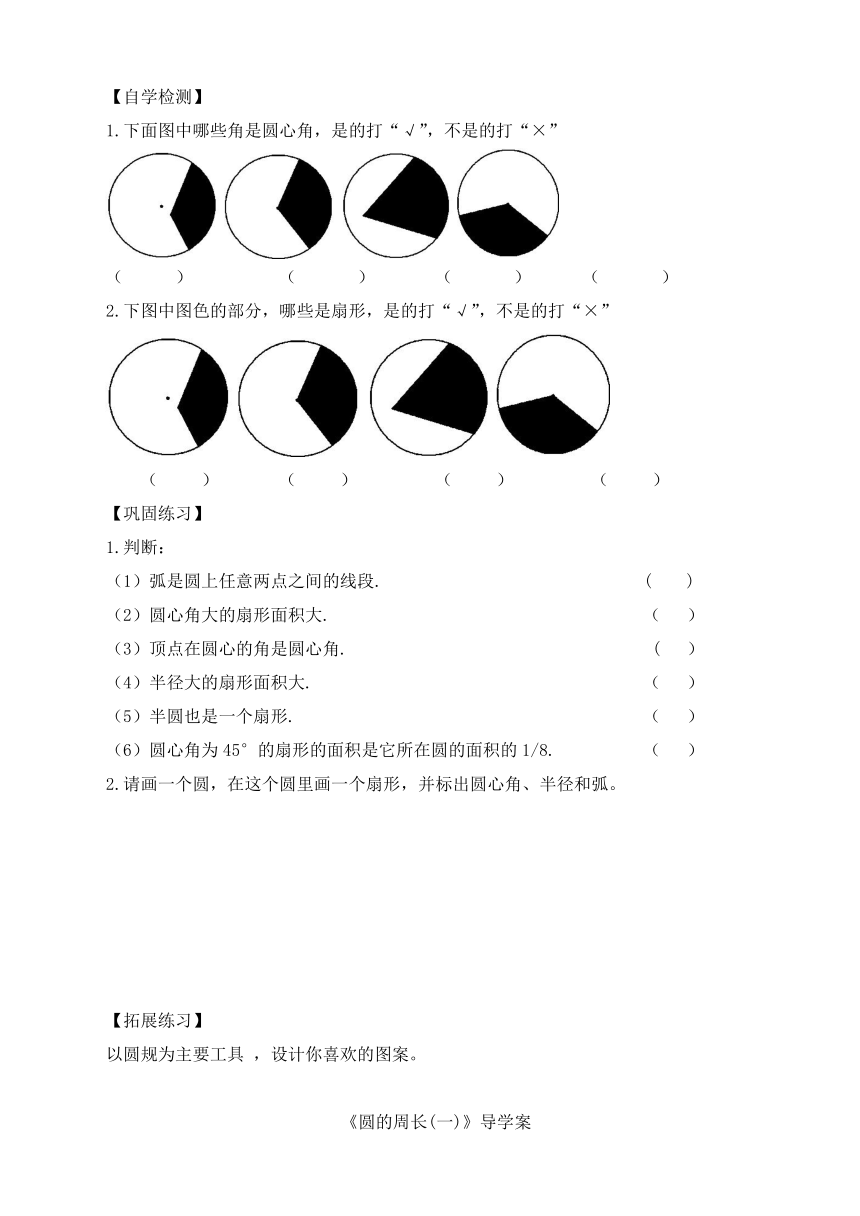
1.下面图中哪些角是圆心角,是的打“√”,不是的打“×”
( ) ( ) ( ) ( )
2.下图中图色的部分,哪些是扇形,是的打“√”,不是的打“×”
( ) ( ) ( ) ( )
【巩固练习】
1.判断:
(1)弧是圆上任意两点之间的线段. ( )
(2)圆心角大的扇形面积大. ( )
(3)顶点在圆心的角是圆心角. ( )
(4)半径大的扇形面积大. ( )
(5)半圆也是一个扇形. ( )
(6)圆心角为45°的扇形的面积是它所在圆的面积的1/8. ( )
2.请画一个圆,在这个圆里画一个扇形,并标出圆心角、半径和弧。
【拓展练习】
以圆规为主要工具 ,设计你喜欢的图案。
《圆的周长(一)》导学案
【学习目标】
1.认识圆的周长,知道圆周率的意义。
2.理解并掌握圆的周长的计算方法,并能正确计算圆的周长。
【温故互查】 请同学们以二人小组完成下列内容。
1.周长是指( )
2.长方形的周长=( );正方形的周长=( )。
【设问导读】
仔细阅读课本16页的内容,同时完成设问导读内容。
1.“铁环滚1圈的距离”是指铁环滚一周的( ),也就是围成圆形铁环的铁丝的( ),也就是圆形铁环的( )。
2.( )叫做圆的周长。
3.从我们的生活实际可知:大铁环滚1圈的距离比小铁环滚1圈的距离( ),也就是半径大的铁环滚一周的距离( );结合圆的大小由半径决定,我们可以猜想圆的周长与圆的( )或( )有关,也就是圆的( )或( )越大,圆的周长就( )。
4.想一想怎样测量圆的周长?说一说你的方法。
方法一:
方法二:
5.拿出准备好的几个大小不同的圆纸板,先测量它们的直径,再测出它们的周长,完成下表。
圆一 圆二 圆三
圆的周长
直径
圆的周长除以直径的商(保留两位小数)
圆的周长总是直径的( ),圆的周长除以直径的商是一个( )的数,把它叫做( ),用希腊字母( )表示。( )一个无限不循环小数,计算时,通常保留( ),取近似值( )。如果用C表示圆的周长,那么C=( )或C=( )。
6.阅读课本28页的数学文化“我国古代杰出的数学家——祖冲之”,说说你的感受。
【自学检测】
1.填表
半径(cm) 直径(cm) 周长(cm)
3
9
2.判断。
(1)一个圆的半径越大,它的周长就越长。 ( )
(2)圆的周长总是直径的3.14倍。 ( )
(3)大圆的圆周率大,小圆的圆周率小。 ( )
(4)∏=3.14 ( )
(5)一个圆的周长等于它半径的2倍。 ( )
(6)半圆的周长等于圆周长的一半。 ( )
【巩固练习】
一、选择题
(1)两个圆的周长不同,是因为( )
A.圆心的位置不同 B.圆周率不同 C.直径长度不同
(2)圆的周长除以直径的商是( )
A.3.14 B. ∏ C.无法确定
(3)用圆规画圆时,两脚之间的距离是4厘米,画出的圆的周长是( )
A.12.56厘米 B.25,12厘米 C.6.28厘米
(4)要求一个圆的周长必须知道( )
A.圆周率 B.直径和半径 C.直径或半径
二、根据所给的条件,分别求出圆的周长。
r=3lcm
d=5dm
三、一个半圆形花坛的半径是6米,它的周长是多少米?
《圆的周长(二)》导学案
【学习目标】
1.进一步掌握圆的周长与直径、半径的关系。
2.掌握已知圆的周长求直径和半径的方法,并能正确计算。
【温故互查】
请同学们以二人小组完成下列内容。
计算下面各圆的周长。
d=25dm
r=0.6m
【设问导读】
一、自学课本17页的例2的内容,同时完成设问导读内容
1. 例2中,车轮是( )形,求车轮转一周自行车前进多少米就是求圆形车轮的( )。已知( ),求圆形车轮的( ),可以直接应用公式( )。
2.独立列式计算,并用估算检查计算结果。
二、自学课本17页的例3的内容,同时完成设问导读内容
1.已知圆形水池的( ),求它的( ),可以利用公式( )列方程解答,求出( )。
2.独立列出方程,解方程,并用估算检查计算结果。
3.还可以怎样算?
4.说说已知圆的周长如何求直径和半径。
圆的直径=( )÷( )
圆的半径=( )÷( )÷( )
【自学检测】
1.一只大钟,它的分针长是40厘米。这根分针的尖端转动一周所走的路程是多少厘米?
2.一个圆形花坛,它的周长是53.38米。这个花坛的半径是多少米?
【巩固练习】
1.根据条件计算各圆的半径。
C=28.26m C=56.52dm
2.公园里有一个圆形草坪,直径为30米,小晶每天早晨绕草坪跑4圈。她每天早晨跑多少米?
3.一根电线长78.5米,正好在一个圆形线圈上绕满10圈,这个线圈的直径是多少米?
【拓展练习】
一个长方形的长16厘米,宽10厘米,在这个长方形里画一个最大的圆,这个圆的周长是多少厘米?
《圆的面积(一)》导学案
【学习目标】
1.知道什么是圆的面积,理解圆的面积计算公式的推导过程。
2.熟记圆的面积计算公式,并能正确运用圆的面积计算公式计算圆的面积。
【温故互查】
请同学们以二人小组完成下列各题(要求:第一题组员给组长讲,第二题组长给组员讲,互相补充纠正)。
1.说一说,我们以前学过哪几种平面图形?并说一说它们的面积的计算公式。
2.说一说,什么是面积?我们用什么方法推导出以前所学平面图形的面积计算公式的?
【设问导读】
自学课本19页—20页的例1、例2的内容,同时完成设问导读内容
1.19页组题图中求这座塔的塔基占地多少平方米?就是求( )。
2.圆的面积就是( )。
3.例1的图一中圆的面积比2个正方形的面积( ),比4个正方形的面积( ),正方形的边长表示为( ),它的面积表示为( ),2个正方形的面积表示为( ),4个正方形的面积表示为( )。
所以,( )<圆的面积<( )。
4.例1的图二中小正方形有( )个方格,圆里大约有( )个方格(非常接近1格的算做1格,其余不足1格的算半格);整个圆里大约有( )格,整个圆里的方格个数是小正方形里的方格个数的( )倍,由此得出,圆的面积是小正方形面积的( ),也就是半径平方的( )。
5.从例2的图中我们可以发现:
(1)把圆等分后拼成一个图形时,等分的份数( ),每一份就会越( ),所拼成的图形越接近于( )。
(2)在拼组图形时,图形的( )没有变化,只是( )改变了,( )的面积等于拼成的近似的( )的面积。
(3)这个近似平行四边形的底相当于( ),用字母表示为( ),平行四边形的高相当于( ),圆的面积等于平行四边形的面积,而平行四边形的面积=底×高=∏r×r,所以圆的面积=( )。
【自学检测】
计算下面各圆的面积。
【巩固练习】
1.判断
(1)圆的面积是半径平方的3.14倍。( )
(2)把一个圆分成若干等份,可以拼成一个近似的平行四边形,这个平行四边形的底是半圆的周长。( )
(3)半径为2厘米的圆,周长与面积相等。( )
(4)一个圆的半径扩大3倍,它的面积就扩大3倍。( )
(5)半圆的周长是这个圆周长的一半,半圆的面积是这个圆面积的一半。( )
2.一个半径是10米的圆形花坛,它的占地面积是多少平方米?
3.某饭店大厅有一只挂钟,分针长40厘米。经过1小时,分针扫过的面积是多少平方厘米?
【拓展练习】
如下图,三角形的面积是6平方米,圆的面积是多少平方米?
《圆的面积(二)》导学案
【学习目标】
1.进一步掌握圆的面积计算方法,能根据圆的直径、周长计算圆的面积。
2.灵活运用圆的面积计算公式解决实际问题。
【温故互查】
请同学们以二人小组完成下列各题
1.根据下面的条件求圆的半径。
d=24cm C=18.84dm
2.根据下面的条件求圆的面积。
r=5dm r=2.5cm
【设问导读】
自学课本20页—21页的例3、例4的内容,同时完成设问导读内容
例3中求鱼池的占地面积就是求一个( )的面积,已知圆形鱼池的( ),
可以直接根据圆的面积公式( )计算。
2.列式计算
3.例4中题目给出的是圆桌的( ),要求圆桌的面积,必须先求出圆桌的( )。
4.列式计算。
5.小结:求圆的面积必须知道圆的( )这个条件,但实际生活中常常不能直接知道( ),如果知道圆的周长或直径,必须先求出圆的( ),再求出圆的面积。
【自学检测】
1.一个圆形花坛的直径是10米,它的占地面积是多少平方米?
2.王家村修了一个周长是251.2米的圆形蓄水池。它的占地面积是多少平方米?
【巩固练习】
1.根据下列条件,求各圆的面积。
(1)r=6m (2)d=14dm (3)C=25.12cm
2.判断
(1)直径相等的两个圆,面积不一定相等。 ( )
(2)圆的周长扩大4倍,它的面积也扩大4倍。 ( )
(3)如果两个圆的面积相等,那么这两个圆的周长也相等。 ( )
3.小明的爸爸放羊时把一只羊栓在木桩上,绳长6米。这只羊能吃到草的面积最大是多少?
4.一根长125.6分米的绳子,正好平行绕一根树干10圈,这根树干横截面的面积是多少平方分米?
《圆的面积(三)》导学案
【学习目标】
1.通过计算窗户的面积,掌握求组合图形的面积的方法。
2.学会从不同的角度去分析解决生活中的问题,思考解决问题的不同策略和方案。
【温故互查】
请同学们以二人小组完成下列各题(要求:第一排组员完成,第二排组长完成,并互相检查纠正)。
计算下面各图形的面积
【设问导读】
自学课本23页的例5的内容,同时完成设问导读内容
1.窗户的上部分是( ),直径是( ),下部分是( ),边长是( )。窗户的面积=( )+( )
2.分步列式计算面积。
3.总结方法:像这种计算组合图形的面积,一般把它分割成几个( ),分别求出( ),再把它们的( )。
【自学检测】
太和村的田径场如下图所示:这个田径场的面积是多少平方米?
【巩固练习】
1.计算环形操场的面积。 2.求下图的面积。
3.在一个长10厘米,宽6厘米的长方形中画一个最大的半圆,这个半圆的面积是多少?
《圆的面积(四)》导学案
【学习目标】
1.能运用圆的面积计算公式,结合生活经验解决实际问题。
2.理解、掌握计算环形面积的方法,并能正确地进行计算。
【设问导读】
自学课本23页-24页的例6的内容,同时完成设问导读内容
1.观察图我们知道:折叠部分的面积=( )。
2.从图中我们知道:正方形的边长未知,无法计算面积,但我们可以把正方形看作( )个相同的( ),也就是说正方形的面积是( )个( )的面积之和。且每个( )的底都是圆的( ),高都是圆的( )。
3.分步列式计算。
4.有一个圆形花坛(如下图),花坛的半径是8米,花坛周围的小路正好2米宽。求小路的面积。
(1)像上图这样的我们叫做圆环。
(2)请利用工具自己做一个圆环。
想想:圆环的面积=( )-( )
(3)观察图我们知道:求小路的面积相当于求( )的面积。
小路的面积=( )。
(4)列式为:
【自学检测】
说出求下面阴影部分面积的解题思路。
【巩固练习】
1.计算下面阴影部分的面积。(单位:厘米)
2一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.在一个周长是18.84厘米的圆内,剪一个最大的正方形。剪去部分的面积是多少平方厘米?
【拓展练习】
如图阴影部分的面积是( )平方厘米。
《圆的整理与复习(一)》导学案
【学习目标】
1.回忆、整理出有关圆的知识网络。
2.进一步巩固圆的有关知识,能解决简单的实际问题。
【回顾整理,构建网络】
自学课本26页的内容,同时完成下面的内容
1.请用圆规画一个半径是1.5厘米的圆,在圆上画出圆心、半径和直径,并用字母标出;再在这个圆中画出一个扇形与圆的一条对称轴。
2.用自己喜欢的方法对本单元的知识进行整理。
3.说说我们是怎样推导出圆的周长和面积计算公式的?
4.回顾我们学过与圆有关的计算公式。
? 知道半径
(r) 知道直径
(d) 知道周长
(C)
求半径(r) ? ? ?
求直径(d) ? ? ?
求周长(C) ? ? ?
求面积(S) ? ? ?
【复习检测】
1.判断
(1)半径是2厘米的圆,周长和面积相等。 ( )
(2)大圆的圆周率比小圆的圆周率大。 ( )
(3)半圆形纸片的周长就是圆周长的一半。 ( )
(4)直径是半径的2倍。 ( )
(5)圆的周长总是该圆直径的3.14倍。 ( )
(6)两个圆的面积相等,它们的直径也相等。 ( )
(7)一个圆的周长扩大到原来的3倍,面积也扩大到原来的3倍。( )
2.填空
(1)一个圆内有( )条直径,( )条半径。( )条直径的长等于2 条半径的长。
(2)周长相等的圆、正方形和长方形,( )的面积最大。
(3)用圆规画一个周长12.56cm的圆,圆规两脚之间的距离是( )cm,所画圆的面积是( )平方厘米。
(4)把一个直径是10cm的圆剪成两个半圆,则两个半圆周长的和是( )cm。
(5)在一张长60cm,宽40cm的长方形纸上剪一个最大的圆,则圆的直径是( )cm,面积是( )cm2。
【巩固练习】
1.填写下表
圆的半径(r) 圆的直径(d) 圆的周长(c) 圆的面积(s)
4cm
10dm
12.56m
2.一幅圆形的书法作品,周长为50.24厘米,那这幅作品的面积有多大?
3.用一条长20米的绳子围绕一颗树的树干绕了6圈,还余下1.16米,这课树的树干的直径约是多少米?
【拓展练习】
沿着半径把一个圆平均分成若干等份后拼成一个近似的长方形,这个长方形的周长是16.56厘米,这个圆的面积是多少平方厘米?
《圆的整理与复习(二)》导学案
【学习目标】
1.进一步熟知和掌握圆的有关知识。
2.能灵活运用圆的周长和面积的有关知识解决生活中的实际问题。
【基础练习】 请同学们以二人小组完成下列各题。
1.根据下面的条件求圆的周长。
(1)r=5cm (2)d=2cm
2.根据下面的条件求圆的面积。
(1)r=2cm (2)d=10cm (3)C=12.56cm
【设问导读】
自学课本26页整理与复习的第2题的内容,同时完成下面的内容。
1.做一道铁箍需要多长的铁丝就是求圆的( ),做一个木盖至少需要多少木板就是求圆的( )。
2.独立列式解答。
【复习检测】
1.小红家的彩板是圆形的,直径是40厘米。如果给彩板周围包一层铝皮,需要多长的铝皮?彩板面的面积是多少?
2.量得一张DVD光盘的周长是37.68厘米,如果要做一个正方形袋子装这张光盘,那么这个正方形袋子的边长至少是多少厘米?
【巩固练习】
1.有一种火车头,它的主动轮的半径是0.75米,如果每分钟转360圈,这个火车头每时行多少千米?(得数保留整数)
2.农家小院里修起了直径是10米的水池,现在准备在水池的周围建一条宽1米的走道,这条走道的面积是多少平方米?
3..求下列各图中阴影的面积
【拓展练习】
下图中,阴影部分的面积是40cm2,求环形面积。
《圆的认识(一)》导学案
【学习目标】
1.掌握画圆的方法,能借助圆规等工具画圆。
2.认识圆,知道圆的各部分名称。
3.掌握圆的特征,理解和掌握在同一个圆里半径和直径的关系。
【设问导读】
仔细阅读课本第12页的例1、例2,同时完成设问导读内容。
1.结合例1中的实物图指出圆在哪里,并说说生活中还有哪些地方有圆。
2.你想到画圆的方法有( )。
用你喜欢的方法在下面画一个圆。
3.画圆时可以用( ),用( )的一只脚( )在( ),另一只脚绕着这个点( )1圈,就画出了一个( )。
4.我们以前学过的平面图形有( ),它们都是由( )围成的;圆是由( )围成的。
5. 画圆时,固定的点是( ),一般用字母( )表示,圆心到圆上任意一点的线段是( ),一般用字母( )表示,通过圆心并且两端都在圆上的线段是( ),一般用字母( )表示。请在你画的圆里标记出圆心、半径和直径。
6.任意画一个圆,剪下来对折几次,量一量、比一比、说一说你发现了什么?
在同一个圆里,半径有( )条,长度都( );在同一个圆里,直径有( )条,长度都( )。
在同一个圆里,直径的长度是半径的( ),半径的长度是直径的( ),用字母表示为( )或( )。
圆是( )图形,每条直径所在的直线都是圆的( ),圆有( )条对称轴。
【自学检测】
用圆规画圆。
画几个圆心在同一点而半径不相等的圆; 画几个圆心不在同一点而半径相等的圆。
2.填表
圆一 圆二 圆三 圆四 圆五
r(m) 3 0.8
2.5
d(m)
6.4 3.6
【巩固练习】
1.判断
(1)圆有无数条对称轴。( )
(2)两端都在圆上的线段,就是直径。( )
(3)在一个圆内所有线段中,直径最长。( )
(4)两条半径相连就是直径。( )
(5)半径为5厘米的圆比直径为6厘米的圆小。( )
2.填空
(1)( )确定圆的位置,( )确定圆的大小,钟表的分针尖端转动一周形成的图形是( ),半径是( )的长度。
(2)在同一个圆里可以画( )直径,( )半径,圆内最长的线段是( )。
(3)在同一个圆中,如果半径是5厘米,那么直径则是( )厘米;如果直径是9厘米,则半径是( )厘米。
(4)画一个直径6厘米的圆,圆规两脚间的距离是( )厘米。
【拓展练习】 画一个半圆,并画出它的对称轴。
《圆的认识(二)》导学案
【学习目标】
1.认识圆心角、弧、扇形,理解并掌握它们的意义。
2.了解扇形的大小与它的圆心角的关系。
3.能用圆设计一些简单的图案。
【温故互查】
请同学们以二人小组完成下列内容(要求:第一题组员给组长讲,第二题组长给组员讲,互相补充纠正)。
1.画圆时,固定的点是( ),它决定圆的( );( )到圆上任意一点的线段是( ),它决定圆的( );通过( )并且两端都在( )的线段是( )。
2.圆有( )条半径,( )条直径;圆是( )图形,它有( )条对称轴;在同一个圆里,所有半径的长度都( ),所有直径的长度都( );在同一个圆里,( )的长度是( )的2倍,( )的长度是( )的一半。
【设问导读】
仔细阅读课本13页-14页的例3、例4,同时完成设问导读内容。
1.( )在圆心的角叫做圆心角;圆上两点之间的部分叫做( );由圆心角的( )和圆心角所对的( )围成的图形是扇形。
2.扇形是( )图形,扇形有( )条对称轴。
3.在同一个圆中,扇形的大小与这个扇形的( )的大小有关;在不同的圆中,扇形的大小与( )和( )有关。
4.想一想:例4中的这些图案中有哪些几何图形?是怎样画出来的?
5.“在正方形中,设计用线段绕成圆的图案”中,正方形的每边是怎样等分的?每边的数是怎样排列的?每条线段连接的顺序又是怎样的?
【自学检测】
1.下面图中哪些角是圆心角,是的打“√”,不是的打“×”
( ) ( ) ( ) ( )
2.下图中图色的部分,哪些是扇形,是的打“√”,不是的打“×”
( ) ( ) ( ) ( )
【巩固练习】
1.判断:
(1)弧是圆上任意两点之间的线段. ( )
(2)圆心角大的扇形面积大. ( )
(3)顶点在圆心的角是圆心角. ( )
(4)半径大的扇形面积大. ( )
(5)半圆也是一个扇形. ( )
(6)圆心角为45°的扇形的面积是它所在圆的面积的1/8. ( )
2.请画一个圆,在这个圆里画一个扇形,并标出圆心角、半径和弧。
【拓展练习】
以圆规为主要工具 ,设计你喜欢的图案。
《圆的周长(一)》导学案
【学习目标】
1.认识圆的周长,知道圆周率的意义。
2.理解并掌握圆的周长的计算方法,并能正确计算圆的周长。
【温故互查】 请同学们以二人小组完成下列内容。
1.周长是指( )
2.长方形的周长=( );正方形的周长=( )。
【设问导读】
仔细阅读课本16页的内容,同时完成设问导读内容。
1.“铁环滚1圈的距离”是指铁环滚一周的( ),也就是围成圆形铁环的铁丝的( ),也就是圆形铁环的( )。
2.( )叫做圆的周长。
3.从我们的生活实际可知:大铁环滚1圈的距离比小铁环滚1圈的距离( ),也就是半径大的铁环滚一周的距离( );结合圆的大小由半径决定,我们可以猜想圆的周长与圆的( )或( )有关,也就是圆的( )或( )越大,圆的周长就( )。
4.想一想怎样测量圆的周长?说一说你的方法。
方法一:
方法二:
5.拿出准备好的几个大小不同的圆纸板,先测量它们的直径,再测出它们的周长,完成下表。
圆一 圆二 圆三
圆的周长
直径
圆的周长除以直径的商(保留两位小数)
圆的周长总是直径的( ),圆的周长除以直径的商是一个( )的数,把它叫做( ),用希腊字母( )表示。( )一个无限不循环小数,计算时,通常保留( ),取近似值( )。如果用C表示圆的周长,那么C=( )或C=( )。
6.阅读课本28页的数学文化“我国古代杰出的数学家——祖冲之”,说说你的感受。
【自学检测】
1.填表
半径(cm) 直径(cm) 周长(cm)
3
9
2.判断。
(1)一个圆的半径越大,它的周长就越长。 ( )
(2)圆的周长总是直径的3.14倍。 ( )
(3)大圆的圆周率大,小圆的圆周率小。 ( )
(4)∏=3.14 ( )
(5)一个圆的周长等于它半径的2倍。 ( )
(6)半圆的周长等于圆周长的一半。 ( )
【巩固练习】
一、选择题
(1)两个圆的周长不同,是因为( )
A.圆心的位置不同 B.圆周率不同 C.直径长度不同
(2)圆的周长除以直径的商是( )
A.3.14 B. ∏ C.无法确定
(3)用圆规画圆时,两脚之间的距离是4厘米,画出的圆的周长是( )
A.12.56厘米 B.25,12厘米 C.6.28厘米
(4)要求一个圆的周长必须知道( )
A.圆周率 B.直径和半径 C.直径或半径
二、根据所给的条件,分别求出圆的周长。
r=3lcm
d=5dm
三、一个半圆形花坛的半径是6米,它的周长是多少米?
《圆的周长(二)》导学案
【学习目标】
1.进一步掌握圆的周长与直径、半径的关系。
2.掌握已知圆的周长求直径和半径的方法,并能正确计算。
【温故互查】
请同学们以二人小组完成下列内容。
计算下面各圆的周长。
d=25dm
r=0.6m
【设问导读】
一、自学课本17页的例2的内容,同时完成设问导读内容
1. 例2中,车轮是( )形,求车轮转一周自行车前进多少米就是求圆形车轮的( )。已知( ),求圆形车轮的( ),可以直接应用公式( )。
2.独立列式计算,并用估算检查计算结果。
二、自学课本17页的例3的内容,同时完成设问导读内容
1.已知圆形水池的( ),求它的( ),可以利用公式( )列方程解答,求出( )。
2.独立列出方程,解方程,并用估算检查计算结果。
3.还可以怎样算?
4.说说已知圆的周长如何求直径和半径。
圆的直径=( )÷( )
圆的半径=( )÷( )÷( )
【自学检测】
1.一只大钟,它的分针长是40厘米。这根分针的尖端转动一周所走的路程是多少厘米?
2.一个圆形花坛,它的周长是53.38米。这个花坛的半径是多少米?
【巩固练习】
1.根据条件计算各圆的半径。
C=28.26m C=56.52dm
2.公园里有一个圆形草坪,直径为30米,小晶每天早晨绕草坪跑4圈。她每天早晨跑多少米?
3.一根电线长78.5米,正好在一个圆形线圈上绕满10圈,这个线圈的直径是多少米?
【拓展练习】
一个长方形的长16厘米,宽10厘米,在这个长方形里画一个最大的圆,这个圆的周长是多少厘米?
《圆的面积(一)》导学案
【学习目标】
1.知道什么是圆的面积,理解圆的面积计算公式的推导过程。
2.熟记圆的面积计算公式,并能正确运用圆的面积计算公式计算圆的面积。
【温故互查】
请同学们以二人小组完成下列各题(要求:第一题组员给组长讲,第二题组长给组员讲,互相补充纠正)。
1.说一说,我们以前学过哪几种平面图形?并说一说它们的面积的计算公式。
2.说一说,什么是面积?我们用什么方法推导出以前所学平面图形的面积计算公式的?
【设问导读】
自学课本19页—20页的例1、例2的内容,同时完成设问导读内容
1.19页组题图中求这座塔的塔基占地多少平方米?就是求( )。
2.圆的面积就是( )。
3.例1的图一中圆的面积比2个正方形的面积( ),比4个正方形的面积( ),正方形的边长表示为( ),它的面积表示为( ),2个正方形的面积表示为( ),4个正方形的面积表示为( )。
所以,( )<圆的面积<( )。
4.例1的图二中小正方形有( )个方格,圆里大约有( )个方格(非常接近1格的算做1格,其余不足1格的算半格);整个圆里大约有( )格,整个圆里的方格个数是小正方形里的方格个数的( )倍,由此得出,圆的面积是小正方形面积的( ),也就是半径平方的( )。
5.从例2的图中我们可以发现:
(1)把圆等分后拼成一个图形时,等分的份数( ),每一份就会越( ),所拼成的图形越接近于( )。
(2)在拼组图形时,图形的( )没有变化,只是( )改变了,( )的面积等于拼成的近似的( )的面积。
(3)这个近似平行四边形的底相当于( ),用字母表示为( ),平行四边形的高相当于( ),圆的面积等于平行四边形的面积,而平行四边形的面积=底×高=∏r×r,所以圆的面积=( )。
【自学检测】
计算下面各圆的面积。
【巩固练习】
1.判断
(1)圆的面积是半径平方的3.14倍。( )
(2)把一个圆分成若干等份,可以拼成一个近似的平行四边形,这个平行四边形的底是半圆的周长。( )
(3)半径为2厘米的圆,周长与面积相等。( )
(4)一个圆的半径扩大3倍,它的面积就扩大3倍。( )
(5)半圆的周长是这个圆周长的一半,半圆的面积是这个圆面积的一半。( )
2.一个半径是10米的圆形花坛,它的占地面积是多少平方米?
3.某饭店大厅有一只挂钟,分针长40厘米。经过1小时,分针扫过的面积是多少平方厘米?
【拓展练习】
如下图,三角形的面积是6平方米,圆的面积是多少平方米?
《圆的面积(二)》导学案
【学习目标】
1.进一步掌握圆的面积计算方法,能根据圆的直径、周长计算圆的面积。
2.灵活运用圆的面积计算公式解决实际问题。
【温故互查】
请同学们以二人小组完成下列各题
1.根据下面的条件求圆的半径。
d=24cm C=18.84dm
2.根据下面的条件求圆的面积。
r=5dm r=2.5cm
【设问导读】
自学课本20页—21页的例3、例4的内容,同时完成设问导读内容
例3中求鱼池的占地面积就是求一个( )的面积,已知圆形鱼池的( ),
可以直接根据圆的面积公式( )计算。
2.列式计算
3.例4中题目给出的是圆桌的( ),要求圆桌的面积,必须先求出圆桌的( )。
4.列式计算。
5.小结:求圆的面积必须知道圆的( )这个条件,但实际生活中常常不能直接知道( ),如果知道圆的周长或直径,必须先求出圆的( ),再求出圆的面积。
【自学检测】
1.一个圆形花坛的直径是10米,它的占地面积是多少平方米?
2.王家村修了一个周长是251.2米的圆形蓄水池。它的占地面积是多少平方米?
【巩固练习】
1.根据下列条件,求各圆的面积。
(1)r=6m (2)d=14dm (3)C=25.12cm
2.判断
(1)直径相等的两个圆,面积不一定相等。 ( )
(2)圆的周长扩大4倍,它的面积也扩大4倍。 ( )
(3)如果两个圆的面积相等,那么这两个圆的周长也相等。 ( )
3.小明的爸爸放羊时把一只羊栓在木桩上,绳长6米。这只羊能吃到草的面积最大是多少?
4.一根长125.6分米的绳子,正好平行绕一根树干10圈,这根树干横截面的面积是多少平方分米?
《圆的面积(三)》导学案
【学习目标】
1.通过计算窗户的面积,掌握求组合图形的面积的方法。
2.学会从不同的角度去分析解决生活中的问题,思考解决问题的不同策略和方案。
【温故互查】
请同学们以二人小组完成下列各题(要求:第一排组员完成,第二排组长完成,并互相检查纠正)。
计算下面各图形的面积
【设问导读】
自学课本23页的例5的内容,同时完成设问导读内容
1.窗户的上部分是( ),直径是( ),下部分是( ),边长是( )。窗户的面积=( )+( )
2.分步列式计算面积。
3.总结方法:像这种计算组合图形的面积,一般把它分割成几个( ),分别求出( ),再把它们的( )。
【自学检测】
太和村的田径场如下图所示:这个田径场的面积是多少平方米?
【巩固练习】
1.计算环形操场的面积。 2.求下图的面积。
3.在一个长10厘米,宽6厘米的长方形中画一个最大的半圆,这个半圆的面积是多少?
《圆的面积(四)》导学案
【学习目标】
1.能运用圆的面积计算公式,结合生活经验解决实际问题。
2.理解、掌握计算环形面积的方法,并能正确地进行计算。
【设问导读】
自学课本23页-24页的例6的内容,同时完成设问导读内容
1.观察图我们知道:折叠部分的面积=( )。
2.从图中我们知道:正方形的边长未知,无法计算面积,但我们可以把正方形看作( )个相同的( ),也就是说正方形的面积是( )个( )的面积之和。且每个( )的底都是圆的( ),高都是圆的( )。
3.分步列式计算。
4.有一个圆形花坛(如下图),花坛的半径是8米,花坛周围的小路正好2米宽。求小路的面积。
(1)像上图这样的我们叫做圆环。
(2)请利用工具自己做一个圆环。
想想:圆环的面积=( )-( )
(3)观察图我们知道:求小路的面积相当于求( )的面积。
小路的面积=( )。
(4)列式为:
【自学检测】
说出求下面阴影部分面积的解题思路。
【巩固练习】
1.计算下面阴影部分的面积。(单位:厘米)
2一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.在一个周长是18.84厘米的圆内,剪一个最大的正方形。剪去部分的面积是多少平方厘米?
【拓展练习】
如图阴影部分的面积是( )平方厘米。
《圆的整理与复习(一)》导学案
【学习目标】
1.回忆、整理出有关圆的知识网络。
2.进一步巩固圆的有关知识,能解决简单的实际问题。
【回顾整理,构建网络】
自学课本26页的内容,同时完成下面的内容
1.请用圆规画一个半径是1.5厘米的圆,在圆上画出圆心、半径和直径,并用字母标出;再在这个圆中画出一个扇形与圆的一条对称轴。
2.用自己喜欢的方法对本单元的知识进行整理。
3.说说我们是怎样推导出圆的周长和面积计算公式的?
4.回顾我们学过与圆有关的计算公式。
? 知道半径
(r) 知道直径
(d) 知道周长
(C)
求半径(r) ? ? ?
求直径(d) ? ? ?
求周长(C) ? ? ?
求面积(S) ? ? ?
【复习检测】
1.判断
(1)半径是2厘米的圆,周长和面积相等。 ( )
(2)大圆的圆周率比小圆的圆周率大。 ( )
(3)半圆形纸片的周长就是圆周长的一半。 ( )
(4)直径是半径的2倍。 ( )
(5)圆的周长总是该圆直径的3.14倍。 ( )
(6)两个圆的面积相等,它们的直径也相等。 ( )
(7)一个圆的周长扩大到原来的3倍,面积也扩大到原来的3倍。( )
2.填空
(1)一个圆内有( )条直径,( )条半径。( )条直径的长等于2 条半径的长。
(2)周长相等的圆、正方形和长方形,( )的面积最大。
(3)用圆规画一个周长12.56cm的圆,圆规两脚之间的距离是( )cm,所画圆的面积是( )平方厘米。
(4)把一个直径是10cm的圆剪成两个半圆,则两个半圆周长的和是( )cm。
(5)在一张长60cm,宽40cm的长方形纸上剪一个最大的圆,则圆的直径是( )cm,面积是( )cm2。
【巩固练习】
1.填写下表
圆的半径(r) 圆的直径(d) 圆的周长(c) 圆的面积(s)
4cm
10dm
12.56m
2.一幅圆形的书法作品,周长为50.24厘米,那这幅作品的面积有多大?
3.用一条长20米的绳子围绕一颗树的树干绕了6圈,还余下1.16米,这课树的树干的直径约是多少米?
【拓展练习】
沿着半径把一个圆平均分成若干等份后拼成一个近似的长方形,这个长方形的周长是16.56厘米,这个圆的面积是多少平方厘米?
《圆的整理与复习(二)》导学案
【学习目标】
1.进一步熟知和掌握圆的有关知识。
2.能灵活运用圆的周长和面积的有关知识解决生活中的实际问题。
【基础练习】 请同学们以二人小组完成下列各题。
1.根据下面的条件求圆的周长。
(1)r=5cm (2)d=2cm
2.根据下面的条件求圆的面积。
(1)r=2cm (2)d=10cm (3)C=12.56cm
【设问导读】
自学课本26页整理与复习的第2题的内容,同时完成下面的内容。
1.做一道铁箍需要多长的铁丝就是求圆的( ),做一个木盖至少需要多少木板就是求圆的( )。
2.独立列式解答。
【复习检测】
1.小红家的彩板是圆形的,直径是40厘米。如果给彩板周围包一层铝皮,需要多长的铝皮?彩板面的面积是多少?
2.量得一张DVD光盘的周长是37.68厘米,如果要做一个正方形袋子装这张光盘,那么这个正方形袋子的边长至少是多少厘米?
【巩固练习】
1.有一种火车头,它的主动轮的半径是0.75米,如果每分钟转360圈,这个火车头每时行多少千米?(得数保留整数)
2.农家小院里修起了直径是10米的水池,现在准备在水池的周围建一条宽1米的走道,这条走道的面积是多少平方米?
3..求下列各图中阴影的面积
【拓展练习】
下图中,阴影部分的面积是40cm2,求环形面积。
