西师大版小学数学六年级上册单元导学案-九、总复习
文档属性
| 名称 | 西师大版小学数学六年级上册单元导学案-九、总复习 |

|
|
| 格式 | doc | ||
| 文件大小 | 277.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 07:20:48 | ||
图片预览




文档简介
九、总复习
《分数乘、除法及分数混合运算的整理复习(一)》导学案
【学习目标】
进一步加深对分数乘除法意义的理解;掌握分数乘除法的计算方法及混合运算的顺序;能运用运算定律和运算性质进行简便计算。
初步学习一些整理数学知识的方法,养成自觉整理的习惯,注重培养自身的分析、比较、概括归纳的能力。
【回顾整理】 根据提示回顾整理分数乘、除法的意义、计算方法及分数混合运算的有关知识。
1、分数乘法:
⑵ 分数乘法的计算方法:
2、分数除法:
⑴ 分数除法的意义:
⑵ 分数除法的计算方法:
分数的混合运算顺序是怎样的?
在同一级运算中,从( );在含有两级的运算中,先算( ),再算( );在含有括号的运算中,先算( ),再算( )。
在简便计算中,我们学过哪些运算定律和运算性质?(分别用字母表示)
运算定律:
运算性质:
【复习检测】
1、填空:
(1) ×12表示( ) 12 ×表示 ( )
( )千克的是1千克;的( )是;7米的与( )米的一样长。
×( )=×( )=-( )=( )×0.3= 1
(3) × ○ × ○ ÷ ○ 7 ÷ ○ 7
(4) 90的是多少?列式为( )
(5) 一个数的是15,这个数是多少?列式为( )
2、选择。
⑴ ×÷×=( )
A 、 1 B 、 C 、
⑵ 图中的双阴影部分意义正确的算式是( )
A、 1 ÷ B、 × C 、 ×
3.计算,注意简便算法的正确使用。
(-÷)× 2--×
(+)÷ ÷ [(+)×2 ]
【拓展训练】
计算:200×200
《分数乘、除法及分数混合运算的整理复习(二)》导学案
【学习目标】
能熟练地在实际的分数问题中找出单位“1”的量,正确分析之间的数量关系,能根据单位“1”是已知还是未知来选择恰当的方法解决问题。
进一步掌握分数应用题的结构特征和解题规律,提高分析问题、解决问题的能力。
【温故互查】
1、用横线标出单位“1”的量。
⑴ 鸭的只数的 相当于鸡的只数。 ⑵ 女生人数占全班人数的 。
⑶ 工厂上月用水12吨,本月节约了。 ⑷ 男生比女生多。
2、只列式不计算
⑴ 商店运来红毛衣25包,蓝毛衣15包,蓝毛衣的包数是红毛衣的几分之几?
⑵ 商店运来红毛衣25包,运来蓝毛衣的包数是红毛衣的 ,商店运来蓝毛衣多少包?
⑶ 商店运来蓝毛衣15包,正好是运来的红毛衣包数的 ,商店运来毛衣多少包?
【回顾整理】
根据上面的练习,完成导读内容。
⑴ 议一议: 你是怎样准确找到分数应用题中的单位“1”的?
⑵ 对于简单分数问题,根据单位“1”已知还是未知,你怎样确定用什么方法来解决该问题?
单位“1”已知,用( );单位“1”未知,用( )或( )。
⑶ 独立完成课本第97页第2题。
2、阅读课本第98页第3题,完成导读内容。
⑴ 想一想,根据图上的信息,求哪个国家的金牌数比较容易?为什么?写出问题,并解答。
⑵ 日本的金牌数与哪个国家的金牌数有关?写出它们之间的数量关系,并解答。
⑶ 议一议:对于稍复杂的分数问题,你会用哪些方法来分析它们之间的数量关系?
【复习检测】
1、仓库运来一批化肥,第一次运出6吨,是总数的,第2次运出余下的。第1次运出6吨是总数的,是把( )看作单位“1“;第2次运出余下的,是把( )看作单位“1”;这批化肥有( )吨,第2次运走( )吨。
2.某品牌电视机现在每台2850元,比原价便宜了,原价多少元?便宜了多少元?
3.一本书,小华第1天读了全书的,第2天读了15页,两天共读了全书的,这本书共有多少页?两天共读了多少页?
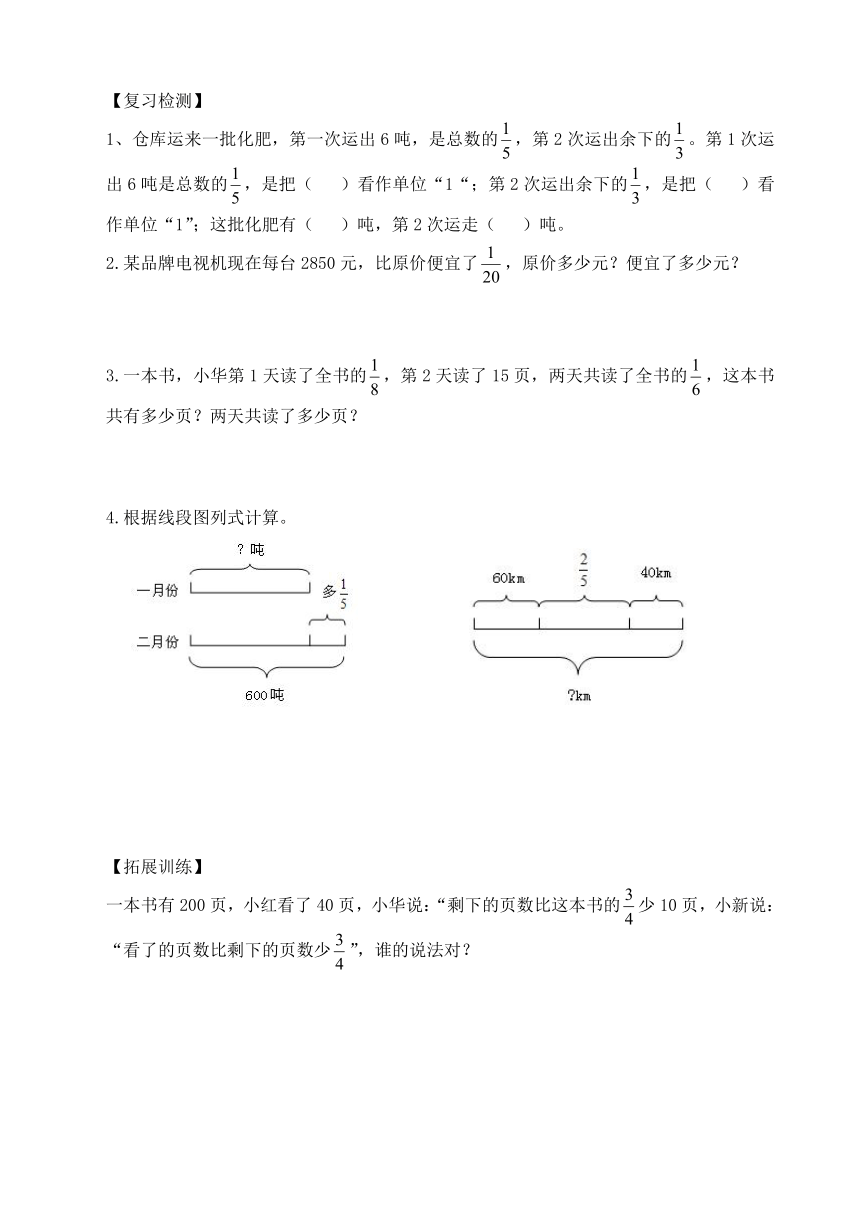
4.根据线段图列式计算。
【拓展训练】
一本书有200页,小红看了40页,小华说:“剩下的页数比这本书的少10页,小新说:“看了的页数比剩下的页数少”,谁的说法对?
《比和按比例分配》导学案
【学习目标】
进一步加深对比的意义的理解,掌握比、分数、除法的联系。
掌握按比例分配问题的特点和解决方法,初步学习整理数学知识的方法。
【回顾整理】
1.仔细阅读课本第98页第4题,你能说出信息中哪两个量的比?比是多少?表示什么意
义?
2.在小组内说说你都了解了哪些关于比的知识?选择你想整理的部分,并把它整理在下面 的知识结构表中。(也可以用你喜欢的方式重新整理)
比 意义:
性质:
求比值 化简比
方法
结果
比与除法、分数的关系
联系 区别
比 前项 比号 后项 比值
除法
分数
3.阅读课本第98页第5题,你能用几种方法解答?
4.议一议:解决按比例分配问题的关键是什么?方法和步骤是怎样的?
关键:找到( )和( )。
方法:
【复习检测】
1.求比值或化简比。
:(化简比) 3㎝:4.2㎞(化简比)
:2(求比值) 1.6:25(求比值)
2.填空:
= 12 : 15 =( )÷10 = 16 ÷( ) =( )
六年级二班男生人数和女生人数的比是5:6,男生人数是女生人数的( ),
女生人数占全班人数的( )。
(3)两个正方形边长的比是2:3,它们周长的比是( ),面积的比是( )。
(4)一个三角形的3内角度数比是2:3:5,按角分是( )三角形。
3、问题解决。
⑴ 将水泥、沙子、石子和水按2:3:5:3的比混合,可以制成混凝土,现有12吨水泥,能生产多少吨混凝土?需要石子多少吨?
⑵ 把一根绳子按3:2的比截成甲、乙两段,
若这根绳子总长8米,甲、乙两段绳子各长几米?
若甲段长4.8米,乙段长几米?
若甲段比乙段长1.6米,这根绳子原来长几米?
⑶ 用一根长120㎝的铁丝焊接成一个长方体框架,它的长、宽、高的比是5:3:2,这个长方 体的长、宽、高各是多少?
【拓展训练】
一条长1800米的路,三天修完,第一天修的长度是第二天修的长度的,第二天修的长度是第三天修的长度的,这三天分别修了多少米?
《圆的整理复习》导学案
【学习目标】
1、进一步学习知识整理的方法。
2、通过复习,加深对圆的特征的理解,能熟练地进行圆的周长与面积的计算,灵活地运用圆的有关知识解决实际问题。
【回顾整理】
1.阅读课本第99页第10题,两人小组议一议下面问题,再按要求画图。
⑴ 画圆时要注意什么?圆规两脚之间的距离是什么?怎么画圆的对称轴?
(画一个半径为2.5㎝的圆,再画出它的一条对称轴。)
⑵ 什么是弧?什么是圆心角?(画一个直径为6㎝的圆,并在其中画出扇形,标明扇形各部分的名称。)
⑶ 根据上面的操作,对圆的特征(包括扇形)的知识进行归纳整理。
圆心 圆心决定:
概 念 特 征
半径
半径决定圆的( ),它有 )条,在同圆、等圆中都( )。
直径
圆的直径有( )条,在同圆、等圆中都( )。
半径、直径的联系 d = r =
圆是轴对称图形 对称轴是:
对称轴条数:
扇形 弧
圆心角
扇形
2.阅读课本99页第11题,完成导读内容。
⑴ 测量哪些条件可以求出圆的周长和面积?
我测出圆的( ),长( )㎝。
圆的周长: 圆的面积:
⑵ 小组内说说:圆的周长和面积有什么区别?计算公式是怎样推导出来的?
3.阅读课本99页第12题, 想一想,这张方桌与它改成的这个最大的圆桌之间有什
么联系?锯下的边角料是不规则的图形,它的面积可以转化为什么来求?
【复习检测】
1、判断:
⑴ 直径是半径的2倍。( )
⑵ 如果一个圆的半径是2分米,那么这个圆的周长和面积相等。( )
⑶ 在连接圆上任意两点的线段中,直径最长。 ( )
⑷ 半圆的面积是圆面积的一半,半圆的周长是圆周长的一半。( )
2、填空:
⑴ 两个圆的半径比是1:3,那么小圆与大圆的直径比是( )周长比是( ),面积比都是( )。
⑵ 一个圆的周长是31.4㎝,它的半径是( )㎝,面积是( )㎝。
问题解决。
⑴ 在一个长8㎝,宽3㎝的长方形里剪下一个最大的圆,圆的面积和周长各是多少?这个长方形里最多能剪几个这样的圆?
⑵ 学校要修建一个周长是25.12米的圆形花坛,并要在它周围铺上一条1米宽的环形小路,这条小路的面积是多少平方米?
【拓展训练】
求阴影部分的面积和周长。
《图形变化和确定位置》导学案
【学习目标】
1、熟练掌握对图形进行放大和缩小变化的方法;能根据方向和距离确定物体的位置。
2、能灵活地运用比例尺的知识解决相关的实际问题。
【回顾整理】
1、阅读课本第100页第13题,完成导读内容。
⑴ 两人小组说说,要算出乌鲁木齐到三亚的实际距离需要知道哪些信息?怎样根据这些信息求实际距离?
⑵ 回顾整理比例尺有关的知识,完成下表。(也可以用你喜欢的方式重新整理)
比
例
尺 意义
计算公式
比例尺= 图上距离=
实际距离=
分类 按形式分 数字比例尺,如:
线段比例尺,如:
按效果分 放大的比例尺,如:
缩小的比例尺,如:
2、阅读课本第100页第14题,完成导读内容。
⑴ 要画出照片的平面图,需要知道什么条件?根据题中的信息怎么计算?
图上长= 图上宽=
⑵ 结合本题实例总结:把图形进行放大和缩小的步骤。(小组合作完成)
3、阅读课本第100页第15题,完成导读内容。
⑴ 要确定体育馆、学校、医院、剧场相对于街心花园的位置,需要知道哪些条件?
需要知道体育馆、学校、医院、剧场相对于街心花园的( )和( )。
⑵ 根据题中的信息完成题中的表格。
【复习检测】
1、填空:
⑴ 七星瓢虫实际长约是5mm,在一幅中,它的长是2.5 cm,这幅图的比例尺是( )。
⑵ 小方家在小明家的东北方,小明家在小方家的( )。
⑶ 看图填空:
2、问题解决。
⑴ 在小可画的平面图上,小可家到学校的实际距离是2 cm,到图书馆的距离是3.5 cm。小可家到学校的实际距离是1100m,小可家到图书馆的距离是多少米?
⑵ 把一个外直径是0.4 cm,内直径是0.3 cm的圆环形铁片,按10:1的比例画出平面图。
⑶ 在比例尺是1:8000000的地图上,量得长江的图上距离是80 cm,那么,在比例尺是1:12000000的地图上,长江的图上距离是多少厘米呢?
【拓展训练】
在比例尺1:5000000的地图上,量得两地距离是24 cm,甲、乙两车同时从两地相向而行,
8时两车相遇,已知甲、乙两车的速度比是3:2,求甲、乙两车的速度各是多少?
《负数的初步认识、可能性》导学案
【学习目标】
1、进一步了解负数的意义,能用正、负数表示意义相反的量。
2、能熟练地用“偶尔”、“经常”、“不可能”“可能”等词语来描述事件发生的可能性。
【回顾整理】
1、阅读课本第99页第8题。
⑴ 组内说说,生活中哪些地方要用负数表示?
⑵ 回顾负数的知识。
① 正、负数的读写:
② 正、负数的意义:用正、负数可以表示( )的量。
③ “0”的再认识:“0”既不是( ),也不是( )。
2、阅读课本第99页第9题,说说表中正数、负数所表示的意义。(两人小组,组内完成)
3、阅读课本第100页第16题,
⑴ 小组内完成。
⑵ 回顾可能性的知识。
① 可能性的大小与数量有关,在总数中所占数量( ),可能性越大;在总数中所占数量( ),可能性越小。
② 确定现象:用( )等词语来描述。
③ 不确定现象:用( )等词语来描述。
【复习检测】
1、填空:
(1) 如果将顺时针旋转记为“+”,那么,逆时针旋转90°应记为( )。
(2)水库的安全水位记作0,超出安全水位8 cm记作+8cm,那么,低于安全水位11cm记作( )。
(3)某地某天的最高气温是9℃,最低气温是-4℃,这天的温差是( )。
(4)在4.5 ,-,0,+,-0.7 , 4 , -2 , 1 中,正数有( )个,负数有( )个,( )既不是正数也不是负数。
(5) 用“偶尔”、“经常”、“不可能”“可能”填空:
⑴ 水( )往高处流。 ⑵ 奶奶身体很虚弱,她( )吃药。
⑶ 今天天空很阴沉,( )会下雨。 ⑷ 爸爸工作不忙,( )会出差。
2、连一连:
袋中有大小相同的20颗棋子,其中有4颗绿色棋子,15颗黄色棋子,从袋中任意摸出1颗棋子。
3、选择:
⑴ 若规定10吨记为0吨,11吨记为+1吨,则下列说法错误的是( )。
A、8吨记为-8吨 B、15吨记为+5吨
C、6吨记为-4吨 D、+3吨表示重量为13吨
⑵ 方便面食品袋上标注着“面饼质量: 120g±5g”,这里的“120g±5g”表示:面饼质量最多不超过( )g,最少不低于( )g,在这个范围内都是符合要求的。
A、115 B、120 C、 125 D、130
4、有8个白球和8个黄球,按要求放8个到一个盒子里,怎么放?
⑴ 摸出的一定是白球。 放( )。
⑵ 摸出的不可能是白球。 放( )。
⑶ 摸出的可能是白球也可能是黄球。 放( )。
⑷ 摸出白球比摸出黄球可能性小。 放( )。
⑸ 经常摸出黄球。 放( )。
⑹ 偶尔摸出黄球。 放( )。
【拓展训练】
以明明家为起点,向东走为正,向西走为负,小明从家走了+600米到了A地,从A地又走了-800米到了B地,那么,B地在小明家的什么方向?距离明明家有多少米?
《分数乘、除法及分数混合运算的整理复习(一)》导学案
【学习目标】
进一步加深对分数乘除法意义的理解;掌握分数乘除法的计算方法及混合运算的顺序;能运用运算定律和运算性质进行简便计算。
初步学习一些整理数学知识的方法,养成自觉整理的习惯,注重培养自身的分析、比较、概括归纳的能力。
【回顾整理】 根据提示回顾整理分数乘、除法的意义、计算方法及分数混合运算的有关知识。
1、分数乘法:
⑵ 分数乘法的计算方法:
2、分数除法:
⑴ 分数除法的意义:
⑵ 分数除法的计算方法:
分数的混合运算顺序是怎样的?
在同一级运算中,从( );在含有两级的运算中,先算( ),再算( );在含有括号的运算中,先算( ),再算( )。
在简便计算中,我们学过哪些运算定律和运算性质?(分别用字母表示)
运算定律:
运算性质:
【复习检测】
1、填空:
(1) ×12表示( ) 12 ×表示 ( )
( )千克的是1千克;的( )是;7米的与( )米的一样长。
×( )=×( )=-( )=( )×0.3= 1
(3) × ○ × ○ ÷ ○ 7 ÷ ○ 7
(4) 90的是多少?列式为( )
(5) 一个数的是15,这个数是多少?列式为( )
2、选择。
⑴ ×÷×=( )
A 、 1 B 、 C 、
⑵ 图中的双阴影部分意义正确的算式是( )
A、 1 ÷ B、 × C 、 ×
3.计算,注意简便算法的正确使用。
(-÷)× 2--×
(+)÷ ÷ [(+)×2 ]
【拓展训练】
计算:200×200
《分数乘、除法及分数混合运算的整理复习(二)》导学案
【学习目标】
能熟练地在实际的分数问题中找出单位“1”的量,正确分析之间的数量关系,能根据单位“1”是已知还是未知来选择恰当的方法解决问题。
进一步掌握分数应用题的结构特征和解题规律,提高分析问题、解决问题的能力。
【温故互查】
1、用横线标出单位“1”的量。
⑴ 鸭的只数的 相当于鸡的只数。 ⑵ 女生人数占全班人数的 。
⑶ 工厂上月用水12吨,本月节约了。 ⑷ 男生比女生多。
2、只列式不计算
⑴ 商店运来红毛衣25包,蓝毛衣15包,蓝毛衣的包数是红毛衣的几分之几?
⑵ 商店运来红毛衣25包,运来蓝毛衣的包数是红毛衣的 ,商店运来蓝毛衣多少包?
⑶ 商店运来蓝毛衣15包,正好是运来的红毛衣包数的 ,商店运来毛衣多少包?
【回顾整理】
根据上面的练习,完成导读内容。
⑴ 议一议: 你是怎样准确找到分数应用题中的单位“1”的?
⑵ 对于简单分数问题,根据单位“1”已知还是未知,你怎样确定用什么方法来解决该问题?
单位“1”已知,用( );单位“1”未知,用( )或( )。
⑶ 独立完成课本第97页第2题。
2、阅读课本第98页第3题,完成导读内容。
⑴ 想一想,根据图上的信息,求哪个国家的金牌数比较容易?为什么?写出问题,并解答。
⑵ 日本的金牌数与哪个国家的金牌数有关?写出它们之间的数量关系,并解答。
⑶ 议一议:对于稍复杂的分数问题,你会用哪些方法来分析它们之间的数量关系?
【复习检测】
1、仓库运来一批化肥,第一次运出6吨,是总数的,第2次运出余下的。第1次运出6吨是总数的,是把( )看作单位“1“;第2次运出余下的,是把( )看作单位“1”;这批化肥有( )吨,第2次运走( )吨。
2.某品牌电视机现在每台2850元,比原价便宜了,原价多少元?便宜了多少元?
3.一本书,小华第1天读了全书的,第2天读了15页,两天共读了全书的,这本书共有多少页?两天共读了多少页?
4.根据线段图列式计算。
【拓展训练】
一本书有200页,小红看了40页,小华说:“剩下的页数比这本书的少10页,小新说:“看了的页数比剩下的页数少”,谁的说法对?
《比和按比例分配》导学案
【学习目标】
进一步加深对比的意义的理解,掌握比、分数、除法的联系。
掌握按比例分配问题的特点和解决方法,初步学习整理数学知识的方法。
【回顾整理】
1.仔细阅读课本第98页第4题,你能说出信息中哪两个量的比?比是多少?表示什么意
义?
2.在小组内说说你都了解了哪些关于比的知识?选择你想整理的部分,并把它整理在下面 的知识结构表中。(也可以用你喜欢的方式重新整理)
比 意义:
性质:
求比值 化简比
方法
结果
比与除法、分数的关系
联系 区别
比 前项 比号 后项 比值
除法
分数
3.阅读课本第98页第5题,你能用几种方法解答?
4.议一议:解决按比例分配问题的关键是什么?方法和步骤是怎样的?
关键:找到( )和( )。
方法:
【复习检测】
1.求比值或化简比。
:(化简比) 3㎝:4.2㎞(化简比)
:2(求比值) 1.6:25(求比值)
2.填空:
= 12 : 15 =( )÷10 = 16 ÷( ) =( )
六年级二班男生人数和女生人数的比是5:6,男生人数是女生人数的( ),
女生人数占全班人数的( )。
(3)两个正方形边长的比是2:3,它们周长的比是( ),面积的比是( )。
(4)一个三角形的3内角度数比是2:3:5,按角分是( )三角形。
3、问题解决。
⑴ 将水泥、沙子、石子和水按2:3:5:3的比混合,可以制成混凝土,现有12吨水泥,能生产多少吨混凝土?需要石子多少吨?
⑵ 把一根绳子按3:2的比截成甲、乙两段,
若这根绳子总长8米,甲、乙两段绳子各长几米?
若甲段长4.8米,乙段长几米?
若甲段比乙段长1.6米,这根绳子原来长几米?
⑶ 用一根长120㎝的铁丝焊接成一个长方体框架,它的长、宽、高的比是5:3:2,这个长方 体的长、宽、高各是多少?
【拓展训练】
一条长1800米的路,三天修完,第一天修的长度是第二天修的长度的,第二天修的长度是第三天修的长度的,这三天分别修了多少米?
《圆的整理复习》导学案
【学习目标】
1、进一步学习知识整理的方法。
2、通过复习,加深对圆的特征的理解,能熟练地进行圆的周长与面积的计算,灵活地运用圆的有关知识解决实际问题。
【回顾整理】
1.阅读课本第99页第10题,两人小组议一议下面问题,再按要求画图。
⑴ 画圆时要注意什么?圆规两脚之间的距离是什么?怎么画圆的对称轴?
(画一个半径为2.5㎝的圆,再画出它的一条对称轴。)
⑵ 什么是弧?什么是圆心角?(画一个直径为6㎝的圆,并在其中画出扇形,标明扇形各部分的名称。)
⑶ 根据上面的操作,对圆的特征(包括扇形)的知识进行归纳整理。
圆心 圆心决定:
概 念 特 征
半径
半径决定圆的( ),它有 )条,在同圆、等圆中都( )。
直径
圆的直径有( )条,在同圆、等圆中都( )。
半径、直径的联系 d = r =
圆是轴对称图形 对称轴是:
对称轴条数:
扇形 弧
圆心角
扇形
2.阅读课本99页第11题,完成导读内容。
⑴ 测量哪些条件可以求出圆的周长和面积?
我测出圆的( ),长( )㎝。
圆的周长: 圆的面积:
⑵ 小组内说说:圆的周长和面积有什么区别?计算公式是怎样推导出来的?
3.阅读课本99页第12题, 想一想,这张方桌与它改成的这个最大的圆桌之间有什
么联系?锯下的边角料是不规则的图形,它的面积可以转化为什么来求?
【复习检测】
1、判断:
⑴ 直径是半径的2倍。( )
⑵ 如果一个圆的半径是2分米,那么这个圆的周长和面积相等。( )
⑶ 在连接圆上任意两点的线段中,直径最长。 ( )
⑷ 半圆的面积是圆面积的一半,半圆的周长是圆周长的一半。( )
2、填空:
⑴ 两个圆的半径比是1:3,那么小圆与大圆的直径比是( )周长比是( ),面积比都是( )。
⑵ 一个圆的周长是31.4㎝,它的半径是( )㎝,面积是( )㎝。
问题解决。
⑴ 在一个长8㎝,宽3㎝的长方形里剪下一个最大的圆,圆的面积和周长各是多少?这个长方形里最多能剪几个这样的圆?
⑵ 学校要修建一个周长是25.12米的圆形花坛,并要在它周围铺上一条1米宽的环形小路,这条小路的面积是多少平方米?
【拓展训练】
求阴影部分的面积和周长。
《图形变化和确定位置》导学案
【学习目标】
1、熟练掌握对图形进行放大和缩小变化的方法;能根据方向和距离确定物体的位置。
2、能灵活地运用比例尺的知识解决相关的实际问题。
【回顾整理】
1、阅读课本第100页第13题,完成导读内容。
⑴ 两人小组说说,要算出乌鲁木齐到三亚的实际距离需要知道哪些信息?怎样根据这些信息求实际距离?
⑵ 回顾整理比例尺有关的知识,完成下表。(也可以用你喜欢的方式重新整理)
比
例
尺 意义
计算公式
比例尺= 图上距离=
实际距离=
分类 按形式分 数字比例尺,如:
线段比例尺,如:
按效果分 放大的比例尺,如:
缩小的比例尺,如:
2、阅读课本第100页第14题,完成导读内容。
⑴ 要画出照片的平面图,需要知道什么条件?根据题中的信息怎么计算?
图上长= 图上宽=
⑵ 结合本题实例总结:把图形进行放大和缩小的步骤。(小组合作完成)
3、阅读课本第100页第15题,完成导读内容。
⑴ 要确定体育馆、学校、医院、剧场相对于街心花园的位置,需要知道哪些条件?
需要知道体育馆、学校、医院、剧场相对于街心花园的( )和( )。
⑵ 根据题中的信息完成题中的表格。
【复习检测】
1、填空:
⑴ 七星瓢虫实际长约是5mm,在一幅中,它的长是2.5 cm,这幅图的比例尺是( )。
⑵ 小方家在小明家的东北方,小明家在小方家的( )。
⑶ 看图填空:
2、问题解决。
⑴ 在小可画的平面图上,小可家到学校的实际距离是2 cm,到图书馆的距离是3.5 cm。小可家到学校的实际距离是1100m,小可家到图书馆的距离是多少米?
⑵ 把一个外直径是0.4 cm,内直径是0.3 cm的圆环形铁片,按10:1的比例画出平面图。
⑶ 在比例尺是1:8000000的地图上,量得长江的图上距离是80 cm,那么,在比例尺是1:12000000的地图上,长江的图上距离是多少厘米呢?
【拓展训练】
在比例尺1:5000000的地图上,量得两地距离是24 cm,甲、乙两车同时从两地相向而行,
8时两车相遇,已知甲、乙两车的速度比是3:2,求甲、乙两车的速度各是多少?
《负数的初步认识、可能性》导学案
【学习目标】
1、进一步了解负数的意义,能用正、负数表示意义相反的量。
2、能熟练地用“偶尔”、“经常”、“不可能”“可能”等词语来描述事件发生的可能性。
【回顾整理】
1、阅读课本第99页第8题。
⑴ 组内说说,生活中哪些地方要用负数表示?
⑵ 回顾负数的知识。
① 正、负数的读写:
② 正、负数的意义:用正、负数可以表示( )的量。
③ “0”的再认识:“0”既不是( ),也不是( )。
2、阅读课本第99页第9题,说说表中正数、负数所表示的意义。(两人小组,组内完成)
3、阅读课本第100页第16题,
⑴ 小组内完成。
⑵ 回顾可能性的知识。
① 可能性的大小与数量有关,在总数中所占数量( ),可能性越大;在总数中所占数量( ),可能性越小。
② 确定现象:用( )等词语来描述。
③ 不确定现象:用( )等词语来描述。
【复习检测】
1、填空:
(1) 如果将顺时针旋转记为“+”,那么,逆时针旋转90°应记为( )。
(2)水库的安全水位记作0,超出安全水位8 cm记作+8cm,那么,低于安全水位11cm记作( )。
(3)某地某天的最高气温是9℃,最低气温是-4℃,这天的温差是( )。
(4)在4.5 ,-,0,+,-0.7 , 4 , -2 , 1 中,正数有( )个,负数有( )个,( )既不是正数也不是负数。
(5) 用“偶尔”、“经常”、“不可能”“可能”填空:
⑴ 水( )往高处流。 ⑵ 奶奶身体很虚弱,她( )吃药。
⑶ 今天天空很阴沉,( )会下雨。 ⑷ 爸爸工作不忙,( )会出差。
2、连一连:
袋中有大小相同的20颗棋子,其中有4颗绿色棋子,15颗黄色棋子,从袋中任意摸出1颗棋子。
3、选择:
⑴ 若规定10吨记为0吨,11吨记为+1吨,则下列说法错误的是( )。
A、8吨记为-8吨 B、15吨记为+5吨
C、6吨记为-4吨 D、+3吨表示重量为13吨
⑵ 方便面食品袋上标注着“面饼质量: 120g±5g”,这里的“120g±5g”表示:面饼质量最多不超过( )g,最少不低于( )g,在这个范围内都是符合要求的。
A、115 B、120 C、 125 D、130
4、有8个白球和8个黄球,按要求放8个到一个盒子里,怎么放?
⑴ 摸出的一定是白球。 放( )。
⑵ 摸出的不可能是白球。 放( )。
⑶ 摸出的可能是白球也可能是黄球。 放( )。
⑷ 摸出白球比摸出黄球可能性小。 放( )。
⑸ 经常摸出黄球。 放( )。
⑹ 偶尔摸出黄球。 放( )。
【拓展训练】
以明明家为起点,向东走为正,向西走为负,小明从家走了+600米到了A地,从A地又走了-800米到了B地,那么,B地在小明家的什么方向?距离明明家有多少米?
同课章节目录
