二次函数中的面积最值问题——水平宽铅垂高 课件(共26张PPT)
文档属性
| 名称 | 二次函数中的面积最值问题——水平宽铅垂高 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 737.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 08:55:16 | ||
图片预览





文档简介
(共26张PPT)
二次函数中的面积最值问题
———
×水平宽×铅垂高
学习目标
1、掌握水平宽铅垂高面积公式:
×水平宽×铅垂高
2、利用公式解决平面直角坐标系中的三边都不与坐标轴平行的三角形面积最值以及四边形面积最值问题;
3、经历计算最大面积问题的探究,体会二次函数是一类最优化问题的数学模型,感受数学的应用价值;
学习准备
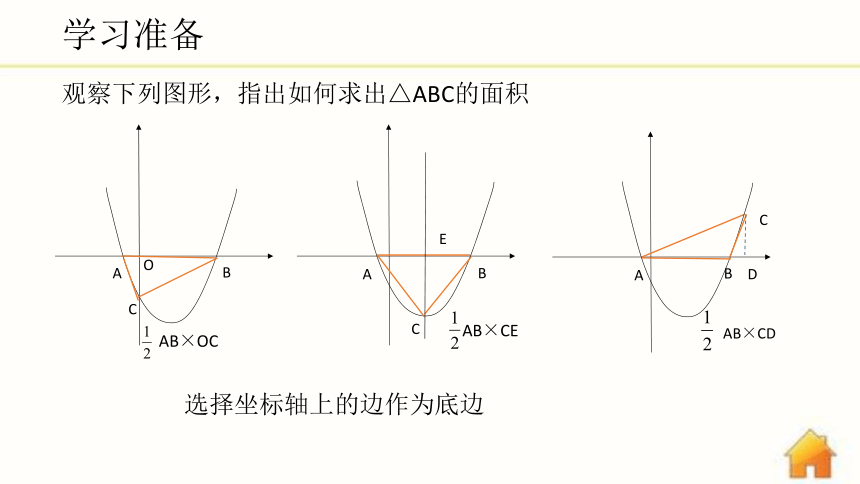
观察下列图形,指出如何求出△ABC的面积
A
B
C
A
B
A
B
C
O
E
D
AB×OC
C
AB×CE
AB×CD
选择坐标轴上的边作为底边
A
B
D
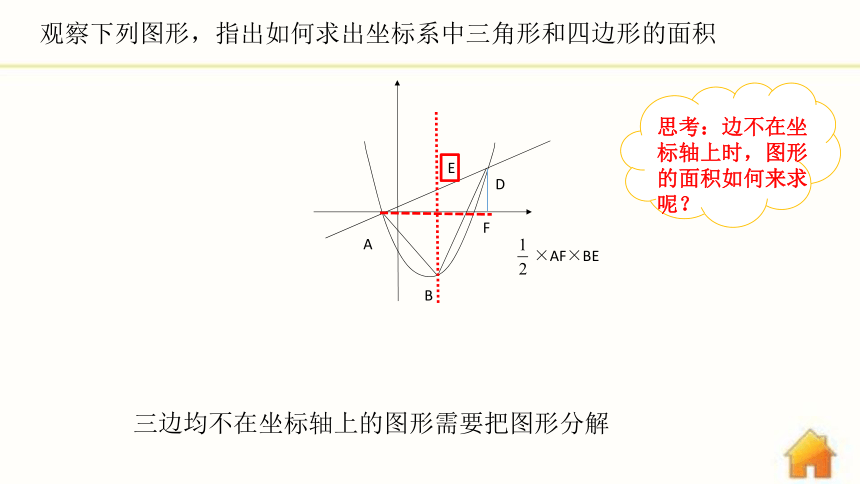
观察下列图形,指出如何求出坐标系中三角形和四边形的面积
E
三边均不在坐标轴上的图形需要把图形分解
F
×AF×BE
思考:边不在坐标轴上时,图形的面积如何来求呢?
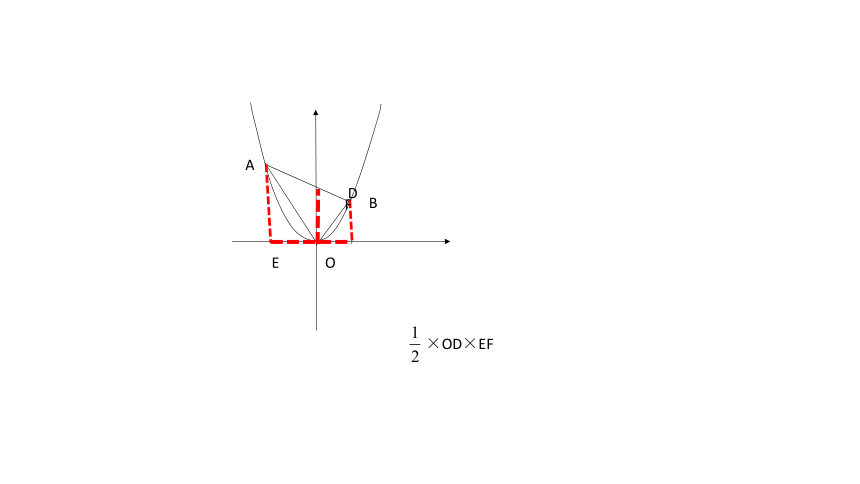
A
D
B
O
×OD×EF
F
E
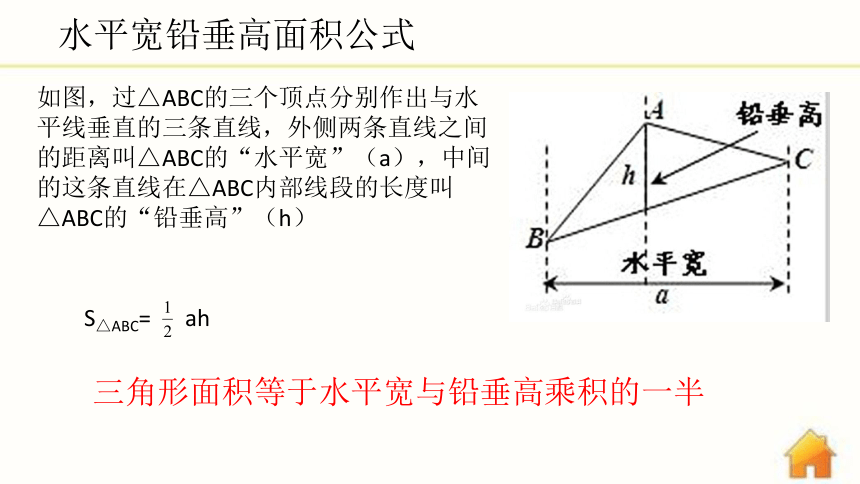
三角形面积等于水平宽与铅垂高乘积的一半
如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h)
S△ABC=
ah
水平宽铅垂高面积公式
如图,在平面直角坐标系中,点A(4,2)、B(2,-2),求三角形AOB的面积?
O
A
B
解:过点B做y轴的平行线交OA于点D
D
设直线OA的关系式为:y=kx
A(4,2),所以k=
∴直线OA的关系式:
y=
x
当x=2时,y=1
∴D(2,1)
∴BD=6
S△AOB=
(4-0)×BD=6
×
三边都不在坐标轴上,如何做辅助线来分割呢?
拓展提升一
三角形面积
(2018?锦州)在平面直角坐标系中,直线y=x﹣2与x轴交于点B,与y轴交于点C,二次函数y=x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;
解:(1)把x=0代y=x﹣2得y=﹣2,∴C(0,﹣2).
把y=0代y=x﹣2得x=4,
∴B(4,0)
设抛物线的解析式为y=(x﹣4)(x﹣m),
将C(0,﹣2)代入得:2m=﹣2,解得:m=﹣1,
∴A(﹣1,0).
∴抛物线的解析式y=(x﹣4)(x+1),即y=
﹣x﹣2.
(2)过点D作y轴的平行线交BC轴于点F
如何作辅助线将△BCD分割呢
F
拓展提升二
四边形面积
(2018?陇南)如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
解:(1)二次函数的解析式为y=﹣x2+2x+3
(2)如图2
P在抛物线上,设P(m,﹣m2+2m+3),
设直线BC的解析式为y=kx+b,
将点B和点C的坐标代入函数解析式得.
解得:
直线BC的解析为y=﹣x+3,
设点Q的坐标为(m,﹣m+3),
PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.
当y=0时,﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
Q
OA=1,
AB=3﹣(﹣1)=4
S四边形ABPC=S△ABC+S△PCQ+S△PBQ
=
AB?OC+
PQ?OF+
PQ?FB
=
×4×3+
(﹣m2+3m)×3
=﹣
(m﹣
)2+
当m=
时,四边形ABPC的面积最大.
当m=
时,﹣m2+2m+3=
即P点的坐标为(
,
).
此时,四边形ACPB的最大面积值为
2019泰安.(13分)若二次函数y=ax2+bx+c的图象与x轴、y轴分别交于点A(3,0)、B(0,﹣2),且过点C(2,﹣2).
(1)求二次函数表达式;
(2)若点P为抛物线上第一象限内的点,且S△PBA=4,求点P的坐标;
(3)在抛物线上(AB下方)是否存在点M,使∠ABO=∠ABM?若存在,求出点M到y轴的距离;若不存在,请说明理由.
---
面积割补
S△PAB
=
S△PBQ
-
S△PAQ.
而△PBQ的底PQ和高易求,△PAQ的底PQ和高易求,可得。
1.[2018·泰安,T24,11分]如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE.
(1)求二次函数的表达式;
中考链接
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
2.[2016·泰安,T28,10分]如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
3.[2015·泰安,T29,12分]如图,抛物线y=ax2+bx+c与x轴的一交点为A(-6,0),与y轴的交点为C(0,3),且经过点G(-2,3).
(1)求抛物线的表达式;
(2)点P是线段OA上一动点,过P作平行于y轴的直线与AC交于点Q,设△CPQ的面积为S,求S的最大值;
对应演练
1、(2013?济南)如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,
OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC.抛物线经过点A、B、C.
(1)求抛物线的解析式.
(2)若点P是第二象限内抛物线上动点,其横坐标为t.
是否存在一点P,使△PCD的面积的最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由.
2(2018?安徽)如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2(1)将A(2,4)与B(6,0)代入y=ax2+bx得
解得
对点演练
(2)如图,过A作x轴的垂直,垂足为D(2,0),连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,
S△OAD=
OD×AD=
×2×4=4;
S△ACD=
AD×CE=
×4×(x?2)=2x?4,
S△BCD=
BD×CF=
×4×(?
+3x)=?
+6x,
则S=S△OAD+S△ACD+S△BCD=?
+8x,
∴S关于x的函数表达式为S=?
+8x(2∵S=S=?
+8x=?
+16,
∴当x=4时,四边形OACB的面积S有最大值,最大值为16.
3、(2018?安岳县二模)如图,抛物线y=﹣x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
对点演练
课堂小结
本节课你有哪些收获?与同学进行交流
谢谢观看!
二次函数中的面积最值问题
———
×水平宽×铅垂高
学习目标
1、掌握水平宽铅垂高面积公式:
×水平宽×铅垂高
2、利用公式解决平面直角坐标系中的三边都不与坐标轴平行的三角形面积最值以及四边形面积最值问题;
3、经历计算最大面积问题的探究,体会二次函数是一类最优化问题的数学模型,感受数学的应用价值;
学习准备
观察下列图形,指出如何求出△ABC的面积
A
B
C
A
B
A
B
C
O
E
D
AB×OC
C
AB×CE
AB×CD
选择坐标轴上的边作为底边
A
B
D
观察下列图形,指出如何求出坐标系中三角形和四边形的面积
E
三边均不在坐标轴上的图形需要把图形分解
F
×AF×BE
思考:边不在坐标轴上时,图形的面积如何来求呢?
A
D
B
O
×OD×EF
F
E
三角形面积等于水平宽与铅垂高乘积的一半
如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h)
S△ABC=
ah
水平宽铅垂高面积公式
如图,在平面直角坐标系中,点A(4,2)、B(2,-2),求三角形AOB的面积?
O
A
B
解:过点B做y轴的平行线交OA于点D
D
设直线OA的关系式为:y=kx
A(4,2),所以k=
∴直线OA的关系式:
y=
x
当x=2时,y=1
∴D(2,1)
∴BD=6
S△AOB=
(4-0)×BD=6
×
三边都不在坐标轴上,如何做辅助线来分割呢?
拓展提升一
三角形面积
(2018?锦州)在平面直角坐标系中,直线y=x﹣2与x轴交于点B,与y轴交于点C,二次函数y=x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;
解:(1)把x=0代y=x﹣2得y=﹣2,∴C(0,﹣2).
把y=0代y=x﹣2得x=4,
∴B(4,0)
设抛物线的解析式为y=(x﹣4)(x﹣m),
将C(0,﹣2)代入得:2m=﹣2,解得:m=﹣1,
∴A(﹣1,0).
∴抛物线的解析式y=(x﹣4)(x+1),即y=
﹣x﹣2.
(2)过点D作y轴的平行线交BC轴于点F
如何作辅助线将△BCD分割呢
F
拓展提升二
四边形面积
(2018?陇南)如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
解:(1)二次函数的解析式为y=﹣x2+2x+3
(2)如图2
P在抛物线上,设P(m,﹣m2+2m+3),
设直线BC的解析式为y=kx+b,
将点B和点C的坐标代入函数解析式得.
解得:
直线BC的解析为y=﹣x+3,
设点Q的坐标为(m,﹣m+3),
PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.
当y=0时,﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
Q
OA=1,
AB=3﹣(﹣1)=4
S四边形ABPC=S△ABC+S△PCQ+S△PBQ
=
AB?OC+
PQ?OF+
PQ?FB
=
×4×3+
(﹣m2+3m)×3
=﹣
(m﹣
)2+
当m=
时,四边形ABPC的面积最大.
当m=
时,﹣m2+2m+3=
即P点的坐标为(
,
).
此时,四边形ACPB的最大面积值为
2019泰安.(13分)若二次函数y=ax2+bx+c的图象与x轴、y轴分别交于点A(3,0)、B(0,﹣2),且过点C(2,﹣2).
(1)求二次函数表达式;
(2)若点P为抛物线上第一象限内的点,且S△PBA=4,求点P的坐标;
(3)在抛物线上(AB下方)是否存在点M,使∠ABO=∠ABM?若存在,求出点M到y轴的距离;若不存在,请说明理由.
---
面积割补
S△PAB
=
S△PBQ
-
S△PAQ.
而△PBQ的底PQ和高易求,△PAQ的底PQ和高易求,可得。
1.[2018·泰安,T24,11分]如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE.
(1)求二次函数的表达式;
中考链接
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
2.[2016·泰安,T28,10分]如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
3.[2015·泰安,T29,12分]如图,抛物线y=ax2+bx+c与x轴的一交点为A(-6,0),与y轴的交点为C(0,3),且经过点G(-2,3).
(1)求抛物线的表达式;
(2)点P是线段OA上一动点,过P作平行于y轴的直线与AC交于点Q,设△CPQ的面积为S,求S的最大值;
对应演练
1、(2013?济南)如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,
OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC.抛物线经过点A、B、C.
(1)求抛物线的解析式.
(2)若点P是第二象限内抛物线上动点,其横坐标为t.
是否存在一点P,使△PCD的面积的最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由.
2(2018?安徽)如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2
解得
对点演练
(2)如图,过A作x轴的垂直,垂足为D(2,0),连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,
S△OAD=
OD×AD=
×2×4=4;
S△ACD=
AD×CE=
×4×(x?2)=2x?4,
S△BCD=
BD×CF=
×4×(?
+3x)=?
+6x,
则S=S△OAD+S△ACD+S△BCD=?
+8x,
∴S关于x的函数表达式为S=?
+8x(2
+8x=?
+16,
∴当x=4时,四边形OACB的面积S有最大值,最大值为16.
3、(2018?安岳县二模)如图,抛物线y=﹣x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
对点演练
课堂小结
本节课你有哪些收获?与同学进行交流
谢谢观看!
