北师大版九年级上册数学 第一章 特殊平行四边形章末复习(ppt,共15张)
文档属性
| 名称 | 北师大版九年级上册数学 第一章 特殊平行四边形章末复习(ppt,共15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 10:00:27 | ||
图片预览





文档简介
特殊平行四边形
章末复习
?
第一章
章末复习
知识归纳
…………….
2
1
巩固应用
…………….
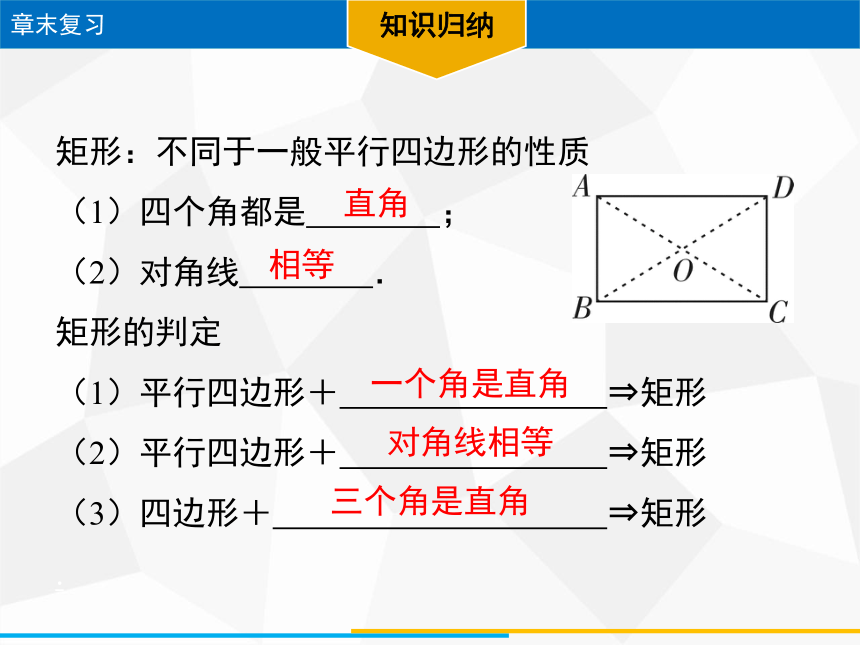
矩形:不同于一般平行四边形的性质
(1)四个角都是 ;
(2)对角线 .
矩形的判定
(1)平行四边形+ ?矩形
(2)平行四边形+ ?矩形
(3)四边形+ ?矩形
.
知识归纳
三个角是直角
直角
相等
一个角是直角
对角线相等
菱形:不同于一般平行四边形的性质
(1)四条边都 ;
(2)对角线 .
菱形的判定
(1)平行四边形+ ?菱形
(2)平行四边形+ ?菱形
(3)四边形+ ?菱形
.
对角线垂直且平分
相等
垂直
邻边相等
对角线垂直
知识归纳
正方形:不同于一般平行四边形的性质
(1)四条边都 ;
(2)四角都是 ;
(3)对角线 .
正方形的判定
(1)矩形+ ?正方形
(2)菱形+ ?正方形
一个角是直角
相等
直角
垂直平分且相等
邻边相等
知识归纳
1.已知菱形的两条对角线的长分别是3 cm,6 cm,则菱形的面积是 cm2.
2.如图,矩形ABCD的对角线AC与BD相交点O,AC=12,P、Q分别为AO、AD的中点,则PQ的长度为 .
9
3
巩固应用
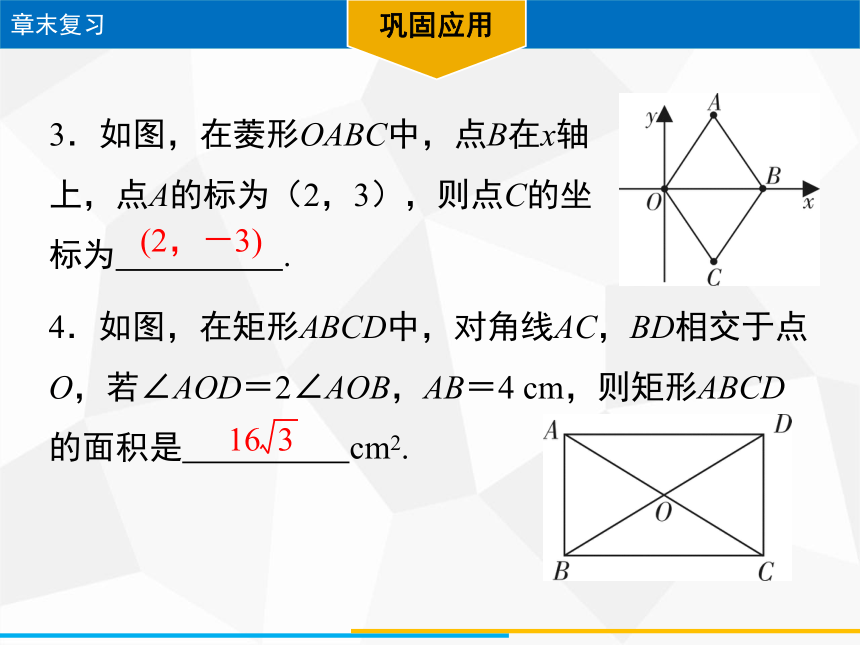
3.如图,在菱形OABC中,点B在x轴
上,点A的标为(2,3),则点C的坐
标为 .
4.如图,在矩形ABCD中,对角线AC,BD相交于点O,若∠AOD=2∠AOB,AB=4 cm,则矩形ABCD的面积是 cm2.
(2,-3)
16 3
巩固应用
5.如图,在正方形ABCD中,∠BAE=60°,AE交对角线BD于点E,那么∠BEC等于( )
A.45° B.60°
C.70° D.75°
6.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT的长为( )
A. 2 B.2 2 C.2 D.1
D
B
巩固应用
7.如图,在四边形ABCD中,AB=
CD,点M,N,P,Q分别是AD,
BC,BD,AC的中点.
求证:MN与PQ互相垂直平分.
证明:连接MP,PN,MQ,NQ
∵M,P是中点∴MP AB.同理NQ AB
∴MP=NQ,MP∥NQ,∴四边形MPNQ是平行四边形
又∵PN= CD AB=CD
∴PN=MP,∴?MPNQ是菱形,∴MN⊥PQ
1
2
1
2
1
2
∥
=
∥
=
巩固应用
8.如图,在△ABC中,AB=BC,BD平
分∠ABC.四边形ABED是平行四边形,
DE交BC于点F,连接CE.
求证:四边形BECD是矩形.
证明:∵AB=BC,BD平分∠ABC
∴BD⊥AC,AD=CD,∵四边形ABED是平行四边形
∴BE∥AD,BE=AD,∴BE=CD
∴四边形BECD是平行四边形
∵BD⊥AC,∴∠BDC=90°,∴?BECD是矩形
巩固应用
9.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于
点N,连接BM,DN.
(1)求证:四边形BMDN是菱形.
(1)证明:∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,∴∠MDO=∠NBO,
在△DMO和△BNO中,
∴△DMO≌△BNO(ASA).∴OM=ON
∵OB=OD,∴四边形BMDN是平行四边形.
∵MN⊥BD,∴?BMDN是菱形
∠MDO=∠NBO
BO=DO
∠MOD=∠NOB
巩固应用
9.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于
点N,连接BM,DN.
(2)若AB=4,AD=8,
求菱形BNDM的周长和对角线MN的长.
(2)解:设MD=MB=x
由勾股定理x2=(8-x)2+42,解得x=5,
∴菱形BNDM的周长为5×4=20,
又BD= =4 5 ∴OB=2 5
∴MN=2MO=2 =2 5
82+42
52-(2 5)2
巩固应用
10.如图,在正方形ABCD中,E是边CD上一点(点E不与点C,D重合),连接BE.取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG;
(1)证明:如图,∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
过点G作GP⊥BC,垂足为P,得矩形ABPG,
∴PG=AB,∠GPF=90°,∠PGF+∠GFP=90°,
∠CBE+∠GFP=90°,
∴∠PGF=∠CBE,PG=CB,∠GPF=∠BCE=90°,
∴△GPF≌△BCE(ASA) ∴BE=FG.
巩固应用
10.如图,在正方形ABCD中,E是边CD上一点(点E不与点C,D重合),连接BE.取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(2)连接CM,若CM=1,试求FG的长.
(2)在Rt△BCE中,
∵点M为BE的中点,∴BE=2,∴FG=BE=2.
答:FG的长为2.
巩固应用
感谢聆听
章末复习
?
第一章
章末复习
知识归纳
…………….
2
1
巩固应用
…………….
矩形:不同于一般平行四边形的性质
(1)四个角都是 ;
(2)对角线 .
矩形的判定
(1)平行四边形+ ?矩形
(2)平行四边形+ ?矩形
(3)四边形+ ?矩形
.
知识归纳
三个角是直角
直角
相等
一个角是直角
对角线相等
菱形:不同于一般平行四边形的性质
(1)四条边都 ;
(2)对角线 .
菱形的判定
(1)平行四边形+ ?菱形
(2)平行四边形+ ?菱形
(3)四边形+ ?菱形
.
对角线垂直且平分
相等
垂直
邻边相等
对角线垂直
知识归纳
正方形:不同于一般平行四边形的性质
(1)四条边都 ;
(2)四角都是 ;
(3)对角线 .
正方形的判定
(1)矩形+ ?正方形
(2)菱形+ ?正方形
一个角是直角
相等
直角
垂直平分且相等
邻边相等
知识归纳
1.已知菱形的两条对角线的长分别是3 cm,6 cm,则菱形的面积是 cm2.
2.如图,矩形ABCD的对角线AC与BD相交点O,AC=12,P、Q分别为AO、AD的中点,则PQ的长度为 .
9
3
巩固应用
3.如图,在菱形OABC中,点B在x轴
上,点A的标为(2,3),则点C的坐
标为 .
4.如图,在矩形ABCD中,对角线AC,BD相交于点O,若∠AOD=2∠AOB,AB=4 cm,则矩形ABCD的面积是 cm2.
(2,-3)
16 3
巩固应用
5.如图,在正方形ABCD中,∠BAE=60°,AE交对角线BD于点E,那么∠BEC等于( )
A.45° B.60°
C.70° D.75°
6.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT的长为( )
A. 2 B.2 2 C.2 D.1
D
B
巩固应用
7.如图,在四边形ABCD中,AB=
CD,点M,N,P,Q分别是AD,
BC,BD,AC的中点.
求证:MN与PQ互相垂直平分.
证明:连接MP,PN,MQ,NQ
∵M,P是中点∴MP AB.同理NQ AB
∴MP=NQ,MP∥NQ,∴四边形MPNQ是平行四边形
又∵PN= CD AB=CD
∴PN=MP,∴?MPNQ是菱形,∴MN⊥PQ
1
2
1
2
1
2
∥
=
∥
=
巩固应用
8.如图,在△ABC中,AB=BC,BD平
分∠ABC.四边形ABED是平行四边形,
DE交BC于点F,连接CE.
求证:四边形BECD是矩形.
证明:∵AB=BC,BD平分∠ABC
∴BD⊥AC,AD=CD,∵四边形ABED是平行四边形
∴BE∥AD,BE=AD,∴BE=CD
∴四边形BECD是平行四边形
∵BD⊥AC,∴∠BDC=90°,∴?BECD是矩形
巩固应用
9.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于
点N,连接BM,DN.
(1)求证:四边形BMDN是菱形.
(1)证明:∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,∴∠MDO=∠NBO,
在△DMO和△BNO中,
∴△DMO≌△BNO(ASA).∴OM=ON
∵OB=OD,∴四边形BMDN是平行四边形.
∵MN⊥BD,∴?BMDN是菱形
∠MDO=∠NBO
BO=DO
∠MOD=∠NOB
巩固应用
9.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于
点N,连接BM,DN.
(2)若AB=4,AD=8,
求菱形BNDM的周长和对角线MN的长.
(2)解:设MD=MB=x
由勾股定理x2=(8-x)2+42,解得x=5,
∴菱形BNDM的周长为5×4=20,
又BD= =4 5 ∴OB=2 5
∴MN=2MO=2 =2 5
82+42
52-(2 5)2
巩固应用
10.如图,在正方形ABCD中,E是边CD上一点(点E不与点C,D重合),连接BE.取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG;
(1)证明:如图,∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
过点G作GP⊥BC,垂足为P,得矩形ABPG,
∴PG=AB,∠GPF=90°,∠PGF+∠GFP=90°,
∠CBE+∠GFP=90°,
∴∠PGF=∠CBE,PG=CB,∠GPF=∠BCE=90°,
∴△GPF≌△BCE(ASA) ∴BE=FG.
巩固应用
10.如图,在正方形ABCD中,E是边CD上一点(点E不与点C,D重合),连接BE.取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(2)连接CM,若CM=1,试求FG的长.
(2)在Rt△BCE中,
∵点M为BE的中点,∴BE=2,∴FG=BE=2.
答:FG的长为2.
巩固应用
感谢聆听
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
