沪科版数学八年级下册 19.1《多边形内角和》课件(共21张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.1《多边形内角和》课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 10:45:14 | ||
图片预览




文档简介
(共21张PPT)
多边形内角和
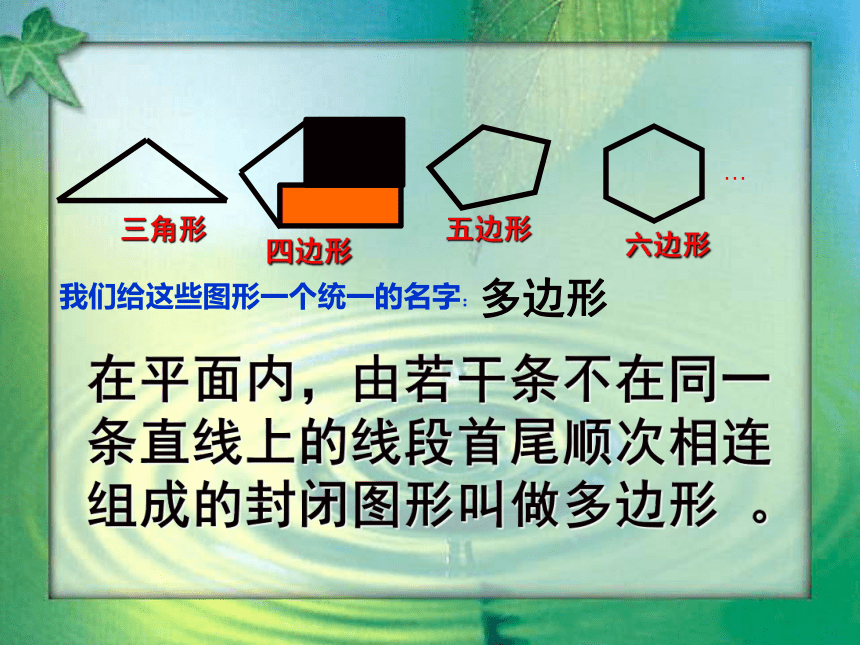
下列图片有没有我们熟悉的几何图形呢?
(3)
(4)
三角形
五边形
六边形
四边形
我们给这些图形一个统一的名字:
多边形
···
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形
。
A
B
C
D
A
B
C
D
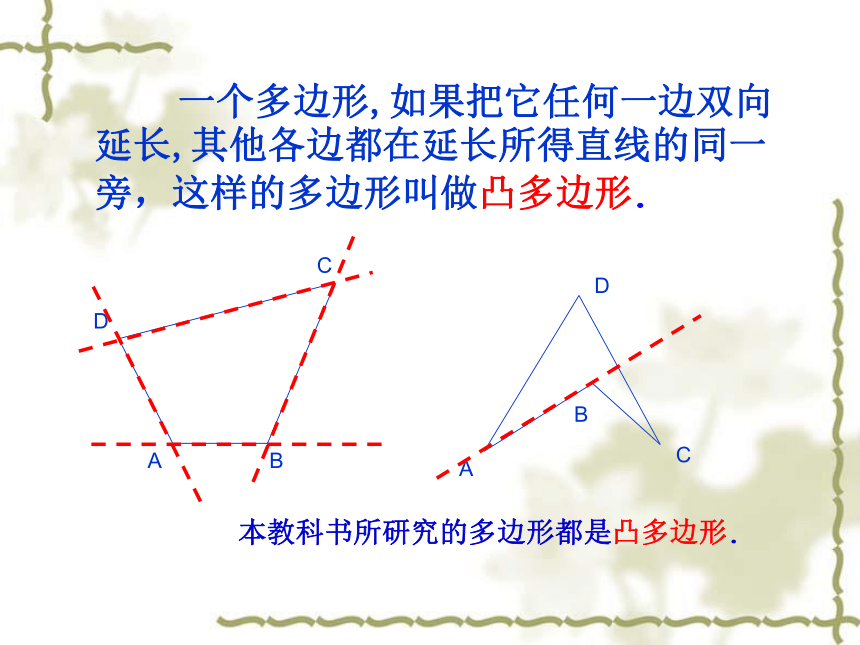
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
本教科书所研究的多边形都是凸多边形.
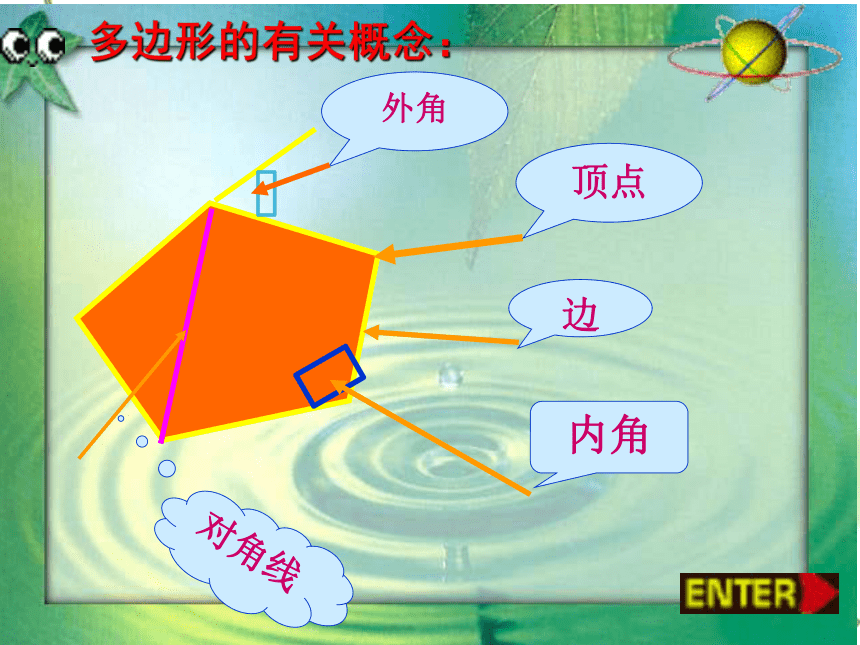
顶点
边
内角
对角线
多边形的有关概念:
外角
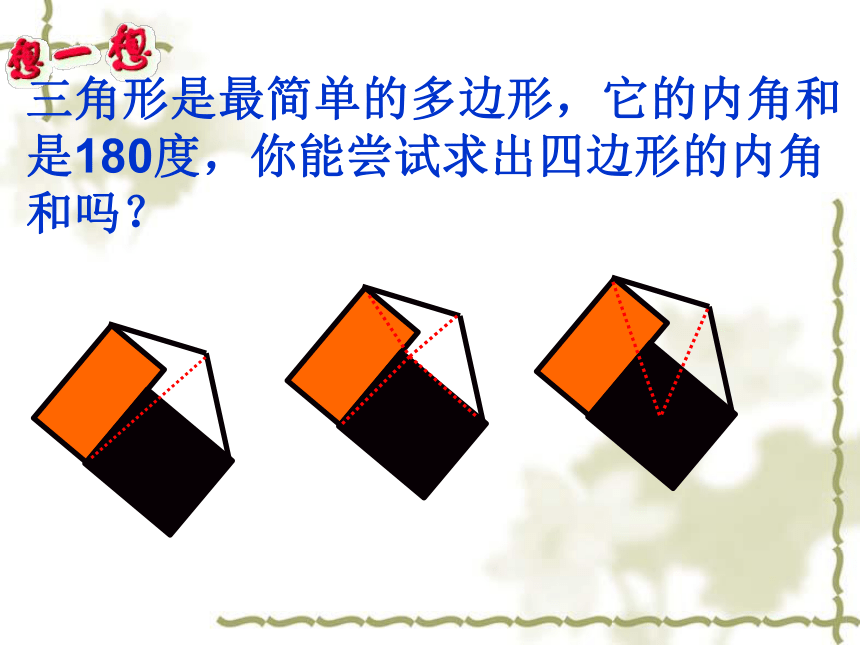
三角形是最简单的多边形,它的内角和
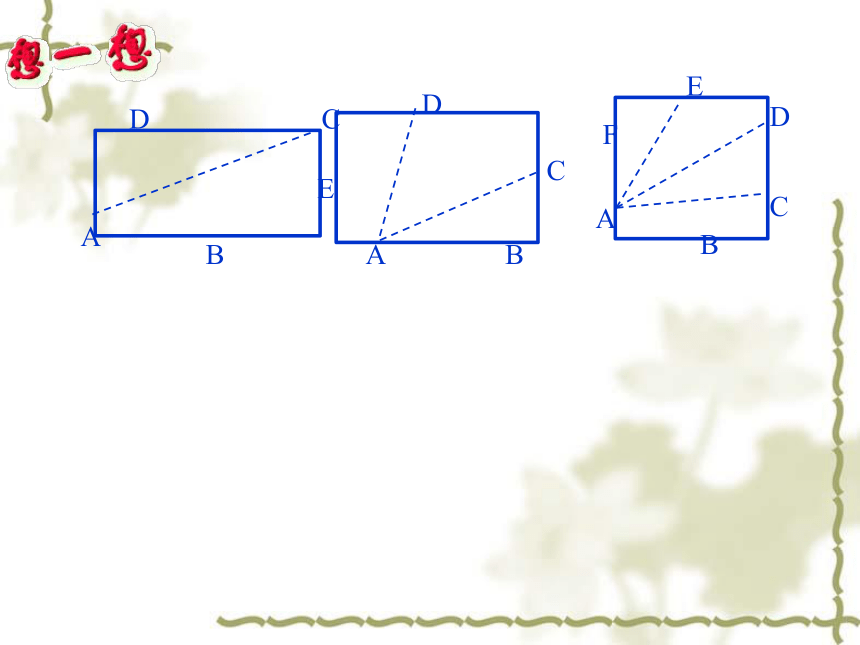
是180度,你能尝试求出四边形的内角和吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
A1
A2
A3
A4
A5
A6
An
A8
A7
探索多边形的内角和
4
5
6
8
n
2×180°
3×180°
4×180°
6×180°
(n-2)×180°
…
…
…
…
4
6
3
2
n-2
n边形内角和公式
(n-2)×1800
你能用另外两种分割法探索多边形内角和吗?
得到定理:
n边形的内角和等于(n-2)·180?.
想一想:
这里的n有没有什么条件?
(n为不小于3的整数)
1、八边形的内角和等于___度.
1080
2、如果一个多边形的内角和是1800
度,那么这是
边形。
十二
解:由多边形的内角和公式可得
(n
-
2)·
180°
=
1800°
(n
-
2)
=
10
n
=
12
∴这是十二边形。
2、2022年我们将在北京举行冬奥会,小明想
制作一个内角和为2022°多边形寄给奥组
委,你能帮他设计吗?
1、已知一个多边形,它的内角和等于五边
形的内角和的2倍,求这个多边形的边数.
1、在四边形ABCD中,∠A=120?,∠B:∠C:∠D
=
3:4:5,求∠B,∠C,∠D的度数。
解:设∠B,∠C,∠D的度数分别是3x
,
4x
,
5x
度,由四边形的内角和等于360?
可得:
120?
+
3x
+
4x
+
5x
=
360?
12x
=
240?
x
=
20?
∴
3x
=
60?
4x
=
80?
5x
=
100?
答:∠B,∠C,∠D的度数分别为60?,80?,
100?
。
2.如果一个n边形的边数增加1,那么它的内角和增加多少度?如果n边形的边数增加1倍,那么它的内角和增加多少度?
本节课收获
通过本节课的学习,你学到了哪些知识?
(2)主要探索了多边形的内角和公式:
(n-2)×180?;
(3)我们还学会了运用多边形内角和公
式进行相关计算。
(1)这节课我们学习了多边形的概念;
多边形的有关概念;多边形的表示方法
提高题:
小明在计算某个多边形的内角和时,由于粗心他漏掉一个内角,求得多边形
的内角和1680°
,你能否求得正确结
果呢?
课本P74,习题19.1第1题.
祝同学们学习进步
多边形内角和
下列图片有没有我们熟悉的几何图形呢?
(3)
(4)
三角形
五边形
六边形
四边形
我们给这些图形一个统一的名字:
多边形
···
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形
。
A
B
C
D
A
B
C
D
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
本教科书所研究的多边形都是凸多边形.
顶点
边
内角
对角线
多边形的有关概念:
外角
三角形是最简单的多边形,它的内角和
是180度,你能尝试求出四边形的内角和吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
A1
A2
A3
A4
A5
A6
An
A8
A7
探索多边形的内角和
4
5
6
8
n
2×180°
3×180°
4×180°
6×180°
(n-2)×180°
…
…
…
…
4
6
3
2
n-2
n边形内角和公式
(n-2)×1800
你能用另外两种分割法探索多边形内角和吗?
得到定理:
n边形的内角和等于(n-2)·180?.
想一想:
这里的n有没有什么条件?
(n为不小于3的整数)
1、八边形的内角和等于___度.
1080
2、如果一个多边形的内角和是1800
度,那么这是
边形。
十二
解:由多边形的内角和公式可得
(n
-
2)·
180°
=
1800°
(n
-
2)
=
10
n
=
12
∴这是十二边形。
2、2022年我们将在北京举行冬奥会,小明想
制作一个内角和为2022°多边形寄给奥组
委,你能帮他设计吗?
1、已知一个多边形,它的内角和等于五边
形的内角和的2倍,求这个多边形的边数.
1、在四边形ABCD中,∠A=120?,∠B:∠C:∠D
=
3:4:5,求∠B,∠C,∠D的度数。
解:设∠B,∠C,∠D的度数分别是3x
,
4x
,
5x
度,由四边形的内角和等于360?
可得:
120?
+
3x
+
4x
+
5x
=
360?
12x
=
240?
x
=
20?
∴
3x
=
60?
4x
=
80?
5x
=
100?
答:∠B,∠C,∠D的度数分别为60?,80?,
100?
。
2.如果一个n边形的边数增加1,那么它的内角和增加多少度?如果n边形的边数增加1倍,那么它的内角和增加多少度?
本节课收获
通过本节课的学习,你学到了哪些知识?
(2)主要探索了多边形的内角和公式:
(n-2)×180?;
(3)我们还学会了运用多边形内角和公
式进行相关计算。
(1)这节课我们学习了多边形的概念;
多边形的有关概念;多边形的表示方法
提高题:
小明在计算某个多边形的内角和时,由于粗心他漏掉一个内角,求得多边形
的内角和1680°
,你能否求得正确结
果呢?
课本P74,习题19.1第1题.
祝同学们学习进步
