13.3 等腰三角形(第二课时 等腰三角形的判定)同步练习题(含答案)
文档属性
| 名称 | 13.3 等腰三角形(第二课时 等腰三角形的判定)同步练习题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十三章 轴对称
13.3 等腰三角形(第二课时 等腰三角形的判定)
练习
一、单选题(共10小题)
1.(2020·无锡市期中)如图,在△ABC中,∠ACB=90°, ∠ABC=60°, BD平分∠ABC ,P点是BD的中点,若AD=6, 则CP的长为( )
A.3.5 B.3 C.4 D.4.5
2.(2019·深圳市期中)如图,在?ABCD中,DE平分∠ADC,AD=8,BE=3,则?ABCD的周长是( )
A.16 B.14 C.26 D.24
3.(2017·淄博市期中)将两块能完全重合的两张等腰直角三角形纸片拼成下列图形:①平行四边形(不包括菱形、矩形、正方形)②矩形③正方形④等边三角形⑤等腰直角三角形( )
A.①③⑤ B.②③⑤ C.①②③ D.①③④⑤
4.(2018·淮南市期末)如图,在□ABCD中,AD=6,AB=4,DE平分∠ADC交BC于点E,则BE的长是( )
A.2 B.3 C.4 D.5
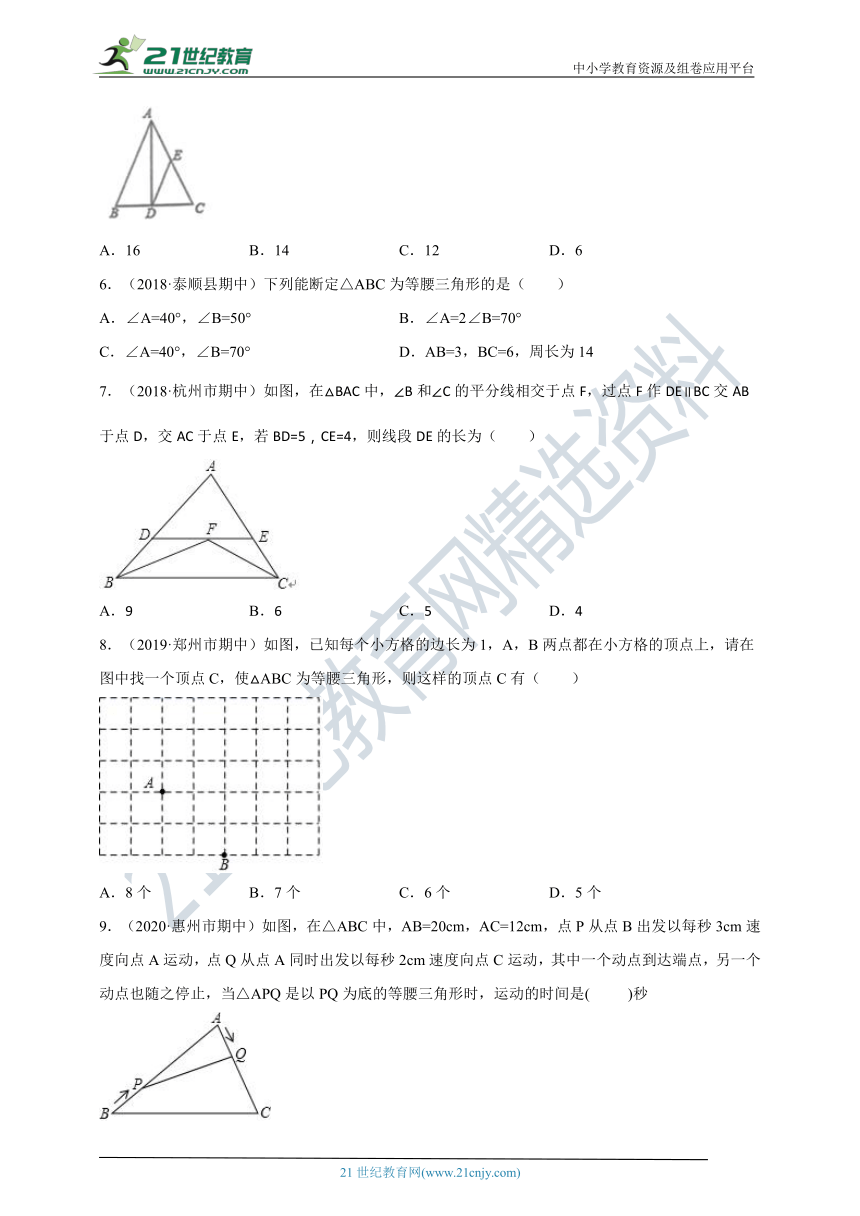
5.(2018达州市期末)如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为21,则BC的长为( )
A.16 B.14 C.12 D.6
6.(2018·泰顺县期中)下列能断定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=2∠B=70°
C.∠A=40°,∠B=70° D.AB=3,BC=6,周长为14
7.(2018·杭州市期中)如图,在△BAC中,∠B和∠C的平分线相交于点F,过点F作DE∥BC交AB于点D,交AC于点E,若BD=5,CE=4,则线段DE的长为( )
?
A.9 B.6 C.5 D.4
8.(2019·郑州市期中)如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
A.8个 B.7个 C.6个 D.5个
9.(2020·惠州市期中)如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是( )秒
A.2.5 B.3 C.3.5 D.4
10.(2018·兴仁市期中)如图,∠AOP=∠BOP=15°,PC//OA,PD⊥OA,若PC=10,则PD等于( ? ? ? ? )
A.10 B.8 C.5 D.2.5
二、填空题(共5小题)
11.(2018·临沭县期末)Rt△ABC中,AC=BC,∠ACB=90°,如图,BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,若S△ABC=32,则△OEF的周长为________.
12.(2020·茂名市期末)在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距_________m.
13.(2019·上饶市期中)如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE//BC,则图中等腰三角形有 个.
14.(2019青岛市期中)如图,在平行四边形ABCD中,已知AD=12cm,AB=8m,AE平分∠BAD交BC边于点E,则CE的长等于_____厘米.
15.(2020·临沧市期末)如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有_____个.
三、解答题(共2小题)
16.(2018·贵阳市期末)如图,在△ABC中,AE是∠BAC的角平分线,交BC于点E,DE∥AB交AC于点D.
(1)求证AD=ED;
(2)若AC=AB,DE=3,求AC的长.
17.(2019·泗阳县期中)如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作DE//BC分别交AB,AC于点D,E.
(1)求证:OD=DB.
(2)若DE=5,求DB+CE的值.
答案
一、单选题(共10小题)
1.B2.C.3.A4.A5.C6.C7.A8.A9.D10.C
二、填空题(共5小题)
11.【答案】8【解析】
∵Rt△ABC中,AC=BC,∠ACB=90°,S△ABC=32,∴BC2=32,解得:BC=8,
∵BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,
∴∠OCF=∠OCA=∠COF,∠EOB=∠OBA=∠OBE,∴OF=CF,OE=BE,
∴△OEF的周长为OF+FE+OE=CF+FE+BE=BC=8.
12.【答案】200【详解】解:由已知得:∠ABC=90°+30°=120°,∠BAC=90°﹣60°=30°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣120°﹣30°=30°,∴∠ACB=∠BAC,
∴BC=AB=200.
【答案】5.【详解】解:∵AB=AC,∠A=36°,∴△ABC是等腰三角形,∠ABC=∠ACB==72°,
∵BD平分∠ABC,∴∠EBD=∠DBC=36°,∵ED∥BC,∴∠AED=∠ADE=72°,∠EDB=∠CBC=36°,
∴在△ADE中,∠AED=∠ADE=72°,AD=AE,△ADE为等腰三角形,
在△ABD中,∠A=∠ABD=36°,AD=BD,△ABD是等腰三角形,
在△BED中,∠EBD=∠EDB=36°,ED=BE,△BED是等腰三角形,
在△BDC中,∠C=∠BDC=72°,BD=BC,△BDC是等腰三角形,
故图中共有5个等腰三角形.
故填5.
14.【答案】4【详解】∵四边形ABCD是平行四边形,∴BC=AD=12cm,AD∥BC,
∴∠DAE=∠BEA,∵AE平分∠BAD,∴∠BAE=∠DAE,
∴∠BEA=∠BAE,∴BE=AB=8cm,∴CE=BC﹣BE=4cm;故答案为:4
15.【答案】4【详解】
(1)当点P在x轴正半轴上,①如图,以OA为腰时,∵A的坐标是(2,2),
∴∠AOP=45°,OA=2,当∠AOP为顶角时,OA=OP=2,当∠OAP为顶角时,AO=AP,
∴OPA=∠AOP=45°,∴∠OAP=90°,∴OP=OA=4,∴P的坐标是(4,0)或(2,0).
②以OA为底边时,∵点A的坐标是(2,2),∴∠AOP=45°,
∵AP=OP,∴∠OAP=∠AOP=45°,∴∠OPA=90°,
∴OP=2,∴P点坐标为(2,0).
(2)当点P在x轴负半轴上,
③以OA为腰时,∵A的坐标是(2,2),
∴OA=2,∴OA=OP=2,∴P的坐标是(﹣2,0).
综上所述:P的坐标是(2,0)或(4,0)或(2,0)或(﹣2,0).
故答案为:4.
三、解答题(共2小题)
16.【答案】(1)证明见解析;(2)6.【详解】证明:(1)∵AE是∠BAC的角平分线
∴∠DAE=∠BAE,∵DE∥AB∴∠DEA=∠EAB,∴∠DAE=∠DEA,∴AD=DE-;
(2)∵AB=AC,AE是∠BAC的角平分线∴AE⊥BC∴∠C+∠CAE=90°,∠CED+∠DEA=90°,
∵∠CAE=∠DEA,∴∠C=∠CED,∴DE=CD, ∴AD=DE=CD=3,∴AC=6.
故答案为(1)证明见解析;(2)6.
17.【答案】(1)见解析(2)5【详解】
(1)∵BO平分∠ABC,∴∠DBO=∠OBC.
∵DE∥BC,∴∠DOB=∠OBC,∴∠DOB=∠DBO,∴OD=DB.
(2)根据(1)得:OD=DB,同理可证:OE=EC,∴BD+EC=DO+OE=DE=5.
_21?????????è?????(www.21cnjy.com)_
第十三章 轴对称
13.3 等腰三角形(第二课时 等腰三角形的判定)
练习
一、单选题(共10小题)
1.(2020·无锡市期中)如图,在△ABC中,∠ACB=90°, ∠ABC=60°, BD平分∠ABC ,P点是BD的中点,若AD=6, 则CP的长为( )
A.3.5 B.3 C.4 D.4.5
2.(2019·深圳市期中)如图,在?ABCD中,DE平分∠ADC,AD=8,BE=3,则?ABCD的周长是( )
A.16 B.14 C.26 D.24
3.(2017·淄博市期中)将两块能完全重合的两张等腰直角三角形纸片拼成下列图形:①平行四边形(不包括菱形、矩形、正方形)②矩形③正方形④等边三角形⑤等腰直角三角形( )
A.①③⑤ B.②③⑤ C.①②③ D.①③④⑤
4.(2018·淮南市期末)如图,在□ABCD中,AD=6,AB=4,DE平分∠ADC交BC于点E,则BE的长是( )
A.2 B.3 C.4 D.5
5.(2018达州市期末)如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为21,则BC的长为( )
A.16 B.14 C.12 D.6
6.(2018·泰顺县期中)下列能断定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=2∠B=70°
C.∠A=40°,∠B=70° D.AB=3,BC=6,周长为14
7.(2018·杭州市期中)如图,在△BAC中,∠B和∠C的平分线相交于点F,过点F作DE∥BC交AB于点D,交AC于点E,若BD=5,CE=4,则线段DE的长为( )
?
A.9 B.6 C.5 D.4
8.(2019·郑州市期中)如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
A.8个 B.7个 C.6个 D.5个
9.(2020·惠州市期中)如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是( )秒
A.2.5 B.3 C.3.5 D.4
10.(2018·兴仁市期中)如图,∠AOP=∠BOP=15°,PC//OA,PD⊥OA,若PC=10,则PD等于( ? ? ? ? )
A.10 B.8 C.5 D.2.5
二、填空题(共5小题)
11.(2018·临沭县期末)Rt△ABC中,AC=BC,∠ACB=90°,如图,BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,若S△ABC=32,则△OEF的周长为________.
12.(2020·茂名市期末)在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距_________m.
13.(2019·上饶市期中)如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE//BC,则图中等腰三角形有 个.
14.(2019青岛市期中)如图,在平行四边形ABCD中,已知AD=12cm,AB=8m,AE平分∠BAD交BC边于点E,则CE的长等于_____厘米.
15.(2020·临沧市期末)如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有_____个.
三、解答题(共2小题)
16.(2018·贵阳市期末)如图,在△ABC中,AE是∠BAC的角平分线,交BC于点E,DE∥AB交AC于点D.
(1)求证AD=ED;
(2)若AC=AB,DE=3,求AC的长.
17.(2019·泗阳县期中)如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作DE//BC分别交AB,AC于点D,E.
(1)求证:OD=DB.
(2)若DE=5,求DB+CE的值.
答案
一、单选题(共10小题)
1.B2.C.3.A4.A5.C6.C7.A8.A9.D10.C
二、填空题(共5小题)
11.【答案】8【解析】
∵Rt△ABC中,AC=BC,∠ACB=90°,S△ABC=32,∴BC2=32,解得:BC=8,
∵BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,
∴∠OCF=∠OCA=∠COF,∠EOB=∠OBA=∠OBE,∴OF=CF,OE=BE,
∴△OEF的周长为OF+FE+OE=CF+FE+BE=BC=8.
12.【答案】200【详解】解:由已知得:∠ABC=90°+30°=120°,∠BAC=90°﹣60°=30°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣120°﹣30°=30°,∴∠ACB=∠BAC,
∴BC=AB=200.
【答案】5.【详解】解:∵AB=AC,∠A=36°,∴△ABC是等腰三角形,∠ABC=∠ACB==72°,
∵BD平分∠ABC,∴∠EBD=∠DBC=36°,∵ED∥BC,∴∠AED=∠ADE=72°,∠EDB=∠CBC=36°,
∴在△ADE中,∠AED=∠ADE=72°,AD=AE,△ADE为等腰三角形,
在△ABD中,∠A=∠ABD=36°,AD=BD,△ABD是等腰三角形,
在△BED中,∠EBD=∠EDB=36°,ED=BE,△BED是等腰三角形,
在△BDC中,∠C=∠BDC=72°,BD=BC,△BDC是等腰三角形,
故图中共有5个等腰三角形.
故填5.
14.【答案】4【详解】∵四边形ABCD是平行四边形,∴BC=AD=12cm,AD∥BC,
∴∠DAE=∠BEA,∵AE平分∠BAD,∴∠BAE=∠DAE,
∴∠BEA=∠BAE,∴BE=AB=8cm,∴CE=BC﹣BE=4cm;故答案为:4
15.【答案】4【详解】
(1)当点P在x轴正半轴上,①如图,以OA为腰时,∵A的坐标是(2,2),
∴∠AOP=45°,OA=2,当∠AOP为顶角时,OA=OP=2,当∠OAP为顶角时,AO=AP,
∴OPA=∠AOP=45°,∴∠OAP=90°,∴OP=OA=4,∴P的坐标是(4,0)或(2,0).
②以OA为底边时,∵点A的坐标是(2,2),∴∠AOP=45°,
∵AP=OP,∴∠OAP=∠AOP=45°,∴∠OPA=90°,
∴OP=2,∴P点坐标为(2,0).
(2)当点P在x轴负半轴上,
③以OA为腰时,∵A的坐标是(2,2),
∴OA=2,∴OA=OP=2,∴P的坐标是(﹣2,0).
综上所述:P的坐标是(2,0)或(4,0)或(2,0)或(﹣2,0).
故答案为:4.
三、解答题(共2小题)
16.【答案】(1)证明见解析;(2)6.【详解】证明:(1)∵AE是∠BAC的角平分线
∴∠DAE=∠BAE,∵DE∥AB∴∠DEA=∠EAB,∴∠DAE=∠DEA,∴AD=DE-;
(2)∵AB=AC,AE是∠BAC的角平分线∴AE⊥BC∴∠C+∠CAE=90°,∠CED+∠DEA=90°,
∵∠CAE=∠DEA,∴∠C=∠CED,∴DE=CD, ∴AD=DE=CD=3,∴AC=6.
故答案为(1)证明见解析;(2)6.
17.【答案】(1)见解析(2)5【详解】
(1)∵BO平分∠ABC,∴∠DBO=∠OBC.
∵DE∥BC,∴∠DOB=∠OBC,∴∠DOB=∠DBO,∴OD=DB.
(2)根据(1)得:OD=DB,同理可证:OE=EC,∴BD+EC=DO+OE=DE=5.
_21?????????è?????(www.21cnjy.com)_
