4.3.2 一次函数的图象 课件(共29张PPT)
文档属性
| 名称 | 4.3.2 一次函数的图象 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 19:44:54 | ||
图片预览



文档简介
(共29张PPT)
数学北师大版
八年级
4.3
一次函数的图象(2)
正比例函数是特殊的一次函数,正比例函数的图象是一条直线,那么一次函数的图象也是一条直线吗?从表达式上看,正比例函数与一次函数相差什么?如果体现在图象上又会有怎样的关系呢?
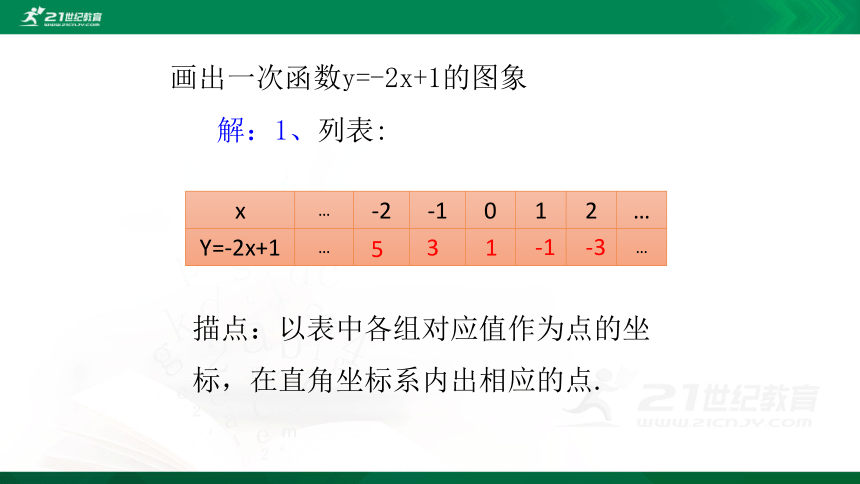
画出一次函数y=-2x+1的图象
解:1、列表:
x
…
-2
-1
0
1
2
…
Y=-2x+1
…
…
5
3
1
-1
-3
描点:以表中各组对应值作为点的坐标,在直角坐标系内出相应的点.
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
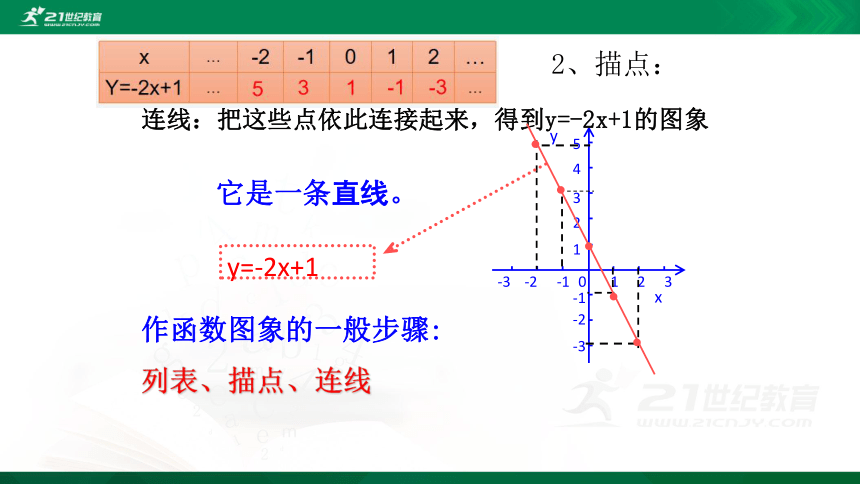
连线:把这些点依此连接起来,得到y=-2x+1的图象
y=-2x+1
它是一条直线。
作函数图象的一般步骤:
列表、描点、连线
2、描点:
一次函数y=
kx
+
b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了,一次函数y=
kx
+
b的图象也称为直线y=kx+b.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
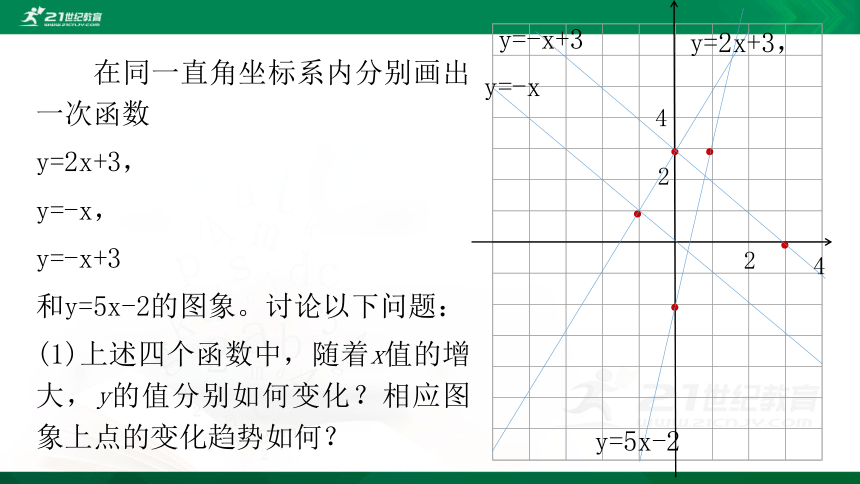
在同一直角坐标系内分别画出一次函数
y=2x+3,
y=-x,
y=-x+3
和y=5x-2的图象。讨论以下问题:
(1)上述四个函数中,随着x值的增大,y的值分别如何变化?相应图象上点的变化趋势如何?
2
4
2
4
?
y=2x+3,
y=-x
y=-x+3
?
?
y=5x-2
y=5x-2
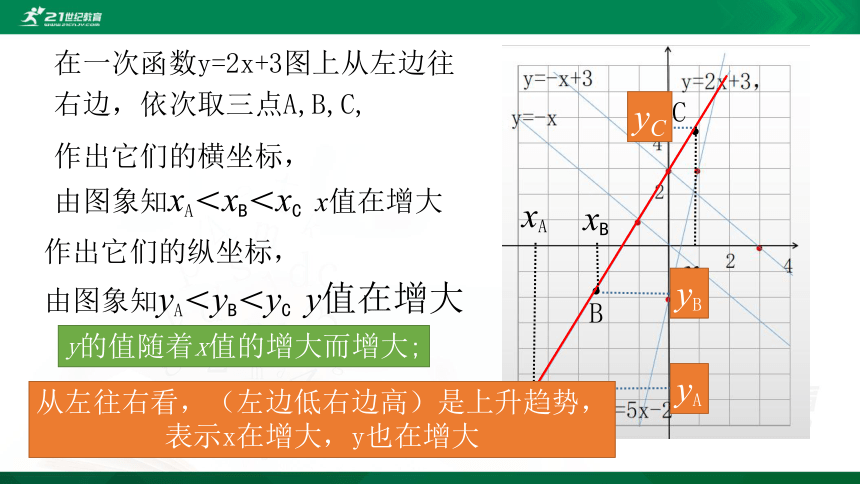
在一次函数y=2x+3图上从左边往右边,依次取三点A,B,C,
?
?
?
A
B
C
作出它们的横坐标,
由图象知xA<xB<xC
x值在增大
xA
xB
xC
作出它们的纵坐标,
由图象知yA<yB<yC
y值在增大
yA
yB
yC
y的值随着x值的增大而增大;
从左往右看,(左边低右边高)是上升趋势,
表示x在增大,y也在增大
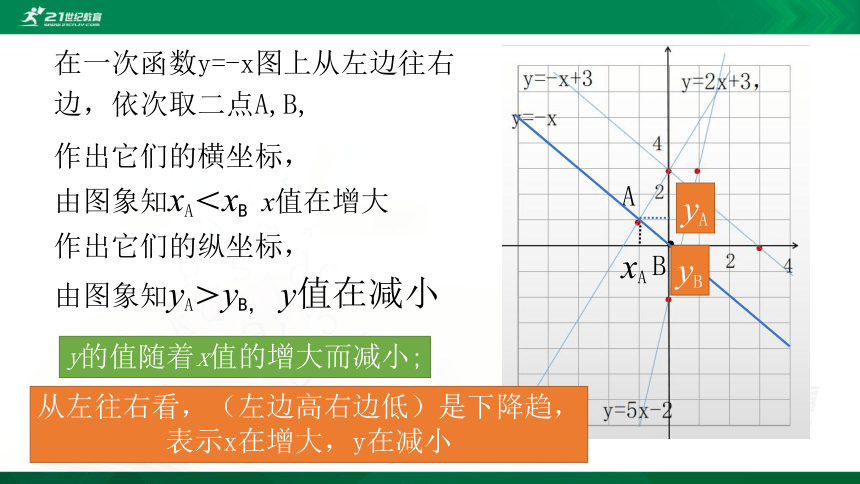
在一次函数y=-x图上从左边往右边,依次取二点A,B,
?
A
B
作出它们的横坐标,
由图象知xA<xB
x值在增大
xA
xB
作出它们的纵坐标,
由图象知yA>yB,
y值在减小
yA
yB
y的值随着x值的增大而减小;
从左往右看,(左边高右边低)是下降趋,
表示x在增大,y在减小
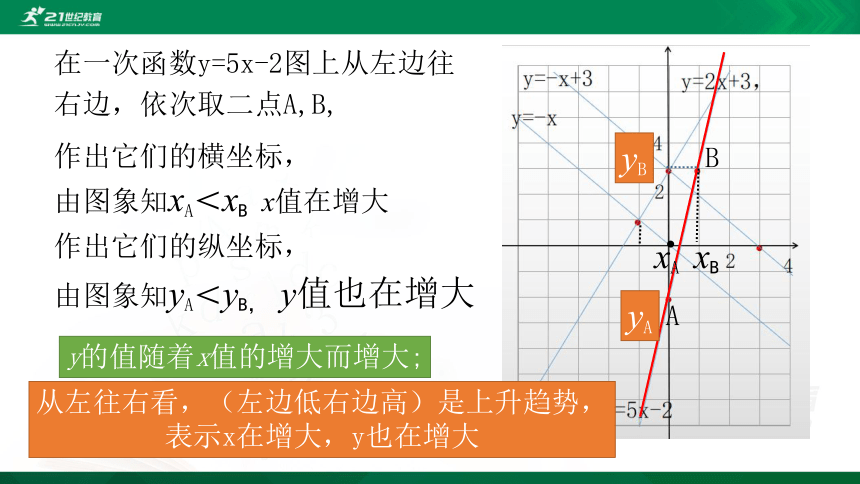
在一次函数y=5x-2图上从左边往右边,依次取二点A,B,
?
A
B
作出它们的横坐标,
由图象知xA<xB
x值在增大
xA
xB
作出它们的纵坐标,
由图象知yA<yB,
y值也在增大
yA
yB
y的值随着x值的增大而增大;
从左往右看,(左边低右边高)是上升趋势,
表示x在增大,y也在增大
在一次函数y=-x+3图上从左边往右边,依次取二点A,B,
?
A
B
作出它们的横坐标,
由图象知xA<xB
x值在增大
xA
xB
作出它们的纵坐标,
由图象知yA>yB,
y值在减小
yA
yB
y的值随着x值的增大而减小;
从左往右看,(左边高右边低)是下降趋,
表示x在增大,y在减小
(1)上述四个函数中,随着x值的增大,y的值分别如何变化?相应图象上点的变化趋势如何?
函数y=2x+3和y=5x-2都是y随x的增大而增大,相应图象上点的位置逐渐升高。
一次函数y=kx+b的图象经过点(0,b)。当k>0时,y的值随着x值的增大而增大;
从左往右看,(左边低右边高)是上升趋势,
表示x在增大,y也在增大
函数y=-x和y=
-x+3都是y随x的增大而减小,相应图象上点的位置逐渐降低.
(1)上述四个函数中,随着x值的增大,y的值分别如何变化?相应图象上点的变化趋势如何?
从左往右看,(左边高右边低)是下降趋,
表示x在增大,y在减小
一次函数y=kx+b的图象经过点(0,b)。当k<0时,y的值随着x值的增大而减小.
一次函数y=kx+b的图象经过点(0,b)。当k>0时,y的值随着x值的增大而增大;当k<0时,y的值随着x值的增大而减小.
越大,图象更陡,越靠近y轴,
y的值变化更大
(2)直线y=-x与y=-x+3的位置关系如何?你能通过适当的移动将直线y=-x变为直线
y=-x+3吗?一般地,直线y=kx+b与y=kx又有怎样的位置关系呢?
答:直线y=-x与直线y=-x+3互相平行,将直线y=-x向上平移3个单位长度就变为直线y=-x+3了。
当k≠0,b≠0或k=0,b≠0时,直线y=kx+b与y=kx平行;当k≠0,b=0或k=0,b=0时,直线y=kx+b与y=kx重合。
1.平移法:直线y=kx+b可以看作由直线y=kx平移得到:
①当b>0时,把直线y=kx向上平移b个单位得到直线y=kx+b;
②当b<0时,把直线y=kx向下平移|b|个单位得到直线y=kx+b.
用一句话来表述就是:“上加下减”;上、下是“形”的平
移,加、减是“数”的变化.
2.直线y=kx+b与坐标轴的交点坐标:
(1)与y轴的交点为(0,b);
(2)与x轴的交点为
.
y=2x-2
m>5
抢答
(3)直线y=2x+3与直线y=-x+3有什么共同点?一般地,你能从函数y=kx+b的图象上直接看出b的数值吗?
答:直线y=
2x+3和直线y=-x+3与y轴相交于同一点(0,3)。直线y=kx+b与y轴交点的纵坐标就是b的值,一般能从函数y=kx+b的图象上直接看出b的数值.
一次函数y=
kx
+
b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了,一次函数y=
kx
+
b的图象也称为直线y=kx+b.
本节知识小结
从左往右看,k>0(左边低右边高)是上升趋势,
表示x在增大,y也在增大
从左往右看,k<0(左边高右边低)是下降趋,
表示x在增大,y在减小
直线y=kx+b与y轴交点的纵坐标就是b的值
一次函数y=kx+b的图象经过点(0,b)。当k>0时,y的值随着x值的增大而增大;当k<0时,y的值随着x值的增大而减小.
越大,图象更陡,越靠近y轴,
y的值变化更大
1.函数y=3x+1的图象与x轴的交点坐标为 ,
与y轴的交点坐标为 .?
(0,1)
2.在同一直角坐标系中,描绘出了下列函数:
①y=-x+1;②y=x+1;③y=-x-1;④y=-2(x+1)的图象,则下列说法正确的是
(
)
A.过点(-1,0)的是①③
B.交点在y轴上的是②④
C.互相平行的是①③
D.关于x轴对称的是①②
C
检测反馈
作业布置:
习题4.2
1,2,3,4,5
选做习题:
1.
一次函数y=x-2的大致图象为(
)
C
2.下列函数中,y的值随x值的增大而增大的函数是(
).
A.y=-2x
B.y=-2x+1
C.y=x-2
D.y=-x-2
C
3.直线y=3x-2可由直线y=3x向
平移
单位得到.
4.直线y=x+2可由直线y=x-1向
平移
单位得到.
下
2
上
3
5.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2
0(填“>”或“<”).
>
6.在同一直角坐标系中画出下列函数的图象.
(1)y=2x+1; (2)y=-2x+1.
y
x
-2
-1
2
1
-2
-1
1
2
o
y=2x+1
y=-2x+1
7.已知一次函数y=(4m+1)x-(m+1).
(1)m为何值时,y随x的增大而减小?
(2)m为何值时,直线与y轴的交点在x轴下方?
解:(1)
∵y随x的增大而减小∴4m+1<0,
∴m<-0.25
解:(2)
∵直线与y轴的交点在x轴下方∴-(m+1)<0,
∴m>-1
1
8.已知k>0,b<0,则一次函数y=kx-b的大致图
象为( )
9.一次函数y=2x+1的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2
A
D
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
八年级
4.3
一次函数的图象(2)
正比例函数是特殊的一次函数,正比例函数的图象是一条直线,那么一次函数的图象也是一条直线吗?从表达式上看,正比例函数与一次函数相差什么?如果体现在图象上又会有怎样的关系呢?
画出一次函数y=-2x+1的图象
解:1、列表:
x
…
-2
-1
0
1
2
…
Y=-2x+1
…
…
5
3
1
-1
-3
描点:以表中各组对应值作为点的坐标,在直角坐标系内出相应的点.
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
连线:把这些点依此连接起来,得到y=-2x+1的图象
y=-2x+1
它是一条直线。
作函数图象的一般步骤:
列表、描点、连线
2、描点:
一次函数y=
kx
+
b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了,一次函数y=
kx
+
b的图象也称为直线y=kx+b.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
在同一直角坐标系内分别画出一次函数
y=2x+3,
y=-x,
y=-x+3
和y=5x-2的图象。讨论以下问题:
(1)上述四个函数中,随着x值的增大,y的值分别如何变化?相应图象上点的变化趋势如何?
2
4
2
4
?
y=2x+3,
y=-x
y=-x+3
?
?
y=5x-2
y=5x-2
在一次函数y=2x+3图上从左边往右边,依次取三点A,B,C,
?
?
?
A
B
C
作出它们的横坐标,
由图象知xA<xB<xC
x值在增大
xA
xB
xC
作出它们的纵坐标,
由图象知yA<yB<yC
y值在增大
yA
yB
yC
y的值随着x值的增大而增大;
从左往右看,(左边低右边高)是上升趋势,
表示x在增大,y也在增大
在一次函数y=-x图上从左边往右边,依次取二点A,B,
?
A
B
作出它们的横坐标,
由图象知xA<xB
x值在增大
xA
xB
作出它们的纵坐标,
由图象知yA>yB,
y值在减小
yA
yB
y的值随着x值的增大而减小;
从左往右看,(左边高右边低)是下降趋,
表示x在增大,y在减小
在一次函数y=5x-2图上从左边往右边,依次取二点A,B,
?
A
B
作出它们的横坐标,
由图象知xA<xB
x值在增大
xA
xB
作出它们的纵坐标,
由图象知yA<yB,
y值也在增大
yA
yB
y的值随着x值的增大而增大;
从左往右看,(左边低右边高)是上升趋势,
表示x在增大,y也在增大
在一次函数y=-x+3图上从左边往右边,依次取二点A,B,
?
A
B
作出它们的横坐标,
由图象知xA<xB
x值在增大
xA
xB
作出它们的纵坐标,
由图象知yA>yB,
y值在减小
yA
yB
y的值随着x值的增大而减小;
从左往右看,(左边高右边低)是下降趋,
表示x在增大,y在减小
(1)上述四个函数中,随着x值的增大,y的值分别如何变化?相应图象上点的变化趋势如何?
函数y=2x+3和y=5x-2都是y随x的增大而增大,相应图象上点的位置逐渐升高。
一次函数y=kx+b的图象经过点(0,b)。当k>0时,y的值随着x值的增大而增大;
从左往右看,(左边低右边高)是上升趋势,
表示x在增大,y也在增大
函数y=-x和y=
-x+3都是y随x的增大而减小,相应图象上点的位置逐渐降低.
(1)上述四个函数中,随着x值的增大,y的值分别如何变化?相应图象上点的变化趋势如何?
从左往右看,(左边高右边低)是下降趋,
表示x在增大,y在减小
一次函数y=kx+b的图象经过点(0,b)。当k<0时,y的值随着x值的增大而减小.
一次函数y=kx+b的图象经过点(0,b)。当k>0时,y的值随着x值的增大而增大;当k<0时,y的值随着x值的增大而减小.
越大,图象更陡,越靠近y轴,
y的值变化更大
(2)直线y=-x与y=-x+3的位置关系如何?你能通过适当的移动将直线y=-x变为直线
y=-x+3吗?一般地,直线y=kx+b与y=kx又有怎样的位置关系呢?
答:直线y=-x与直线y=-x+3互相平行,将直线y=-x向上平移3个单位长度就变为直线y=-x+3了。
当k≠0,b≠0或k=0,b≠0时,直线y=kx+b与y=kx平行;当k≠0,b=0或k=0,b=0时,直线y=kx+b与y=kx重合。
1.平移法:直线y=kx+b可以看作由直线y=kx平移得到:
①当b>0时,把直线y=kx向上平移b个单位得到直线y=kx+b;
②当b<0时,把直线y=kx向下平移|b|个单位得到直线y=kx+b.
用一句话来表述就是:“上加下减”;上、下是“形”的平
移,加、减是“数”的变化.
2.直线y=kx+b与坐标轴的交点坐标:
(1)与y轴的交点为(0,b);
(2)与x轴的交点为
.
y=2x-2
m>5
抢答
(3)直线y=2x+3与直线y=-x+3有什么共同点?一般地,你能从函数y=kx+b的图象上直接看出b的数值吗?
答:直线y=
2x+3和直线y=-x+3与y轴相交于同一点(0,3)。直线y=kx+b与y轴交点的纵坐标就是b的值,一般能从函数y=kx+b的图象上直接看出b的数值.
一次函数y=
kx
+
b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了,一次函数y=
kx
+
b的图象也称为直线y=kx+b.
本节知识小结
从左往右看,k>0(左边低右边高)是上升趋势,
表示x在增大,y也在增大
从左往右看,k<0(左边高右边低)是下降趋,
表示x在增大,y在减小
直线y=kx+b与y轴交点的纵坐标就是b的值
一次函数y=kx+b的图象经过点(0,b)。当k>0时,y的值随着x值的增大而增大;当k<0时,y的值随着x值的增大而减小.
越大,图象更陡,越靠近y轴,
y的值变化更大
1.函数y=3x+1的图象与x轴的交点坐标为 ,
与y轴的交点坐标为 .?
(0,1)
2.在同一直角坐标系中,描绘出了下列函数:
①y=-x+1;②y=x+1;③y=-x-1;④y=-2(x+1)的图象,则下列说法正确的是
(
)
A.过点(-1,0)的是①③
B.交点在y轴上的是②④
C.互相平行的是①③
D.关于x轴对称的是①②
C
检测反馈
作业布置:
习题4.2
1,2,3,4,5
选做习题:
1.
一次函数y=x-2的大致图象为(
)
C
2.下列函数中,y的值随x值的增大而增大的函数是(
).
A.y=-2x
B.y=-2x+1
C.y=x-2
D.y=-x-2
C
3.直线y=3x-2可由直线y=3x向
平移
单位得到.
4.直线y=x+2可由直线y=x-1向
平移
单位得到.
下
2
上
3
5.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1-y2
0(填“>”或“<”).
>
6.在同一直角坐标系中画出下列函数的图象.
(1)y=2x+1; (2)y=-2x+1.
y
x
-2
-1
2
1
-2
-1
1
2
o
y=2x+1
y=-2x+1
7.已知一次函数y=(4m+1)x-(m+1).
(1)m为何值时,y随x的增大而减小?
(2)m为何值时,直线与y轴的交点在x轴下方?
解:(1)
∵y随x的增大而减小∴4m+1<0,
∴m<-0.25
解:(2)
∵直线与y轴的交点在x轴下方∴-(m+1)<0,
∴m>-1
1
8.已知k>0,b<0,则一次函数y=kx-b的大致图
象为( )
9.一次函数y=2x+1的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2
A
D
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
