4.4.1 一次函数的应用 课件(共21张PPT)
文档属性
| 名称 | 4.4.1 一次函数的应用 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 19:48:59 | ||
图片预览





文档简介
(共21张PPT)
数学北师大版
八年级
4
一次函数的应用(第1课时)
4
一次函数的应用(1)
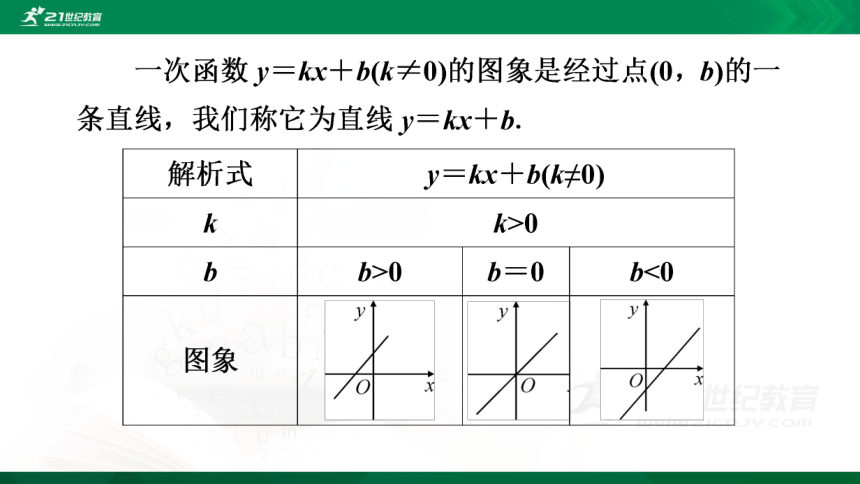
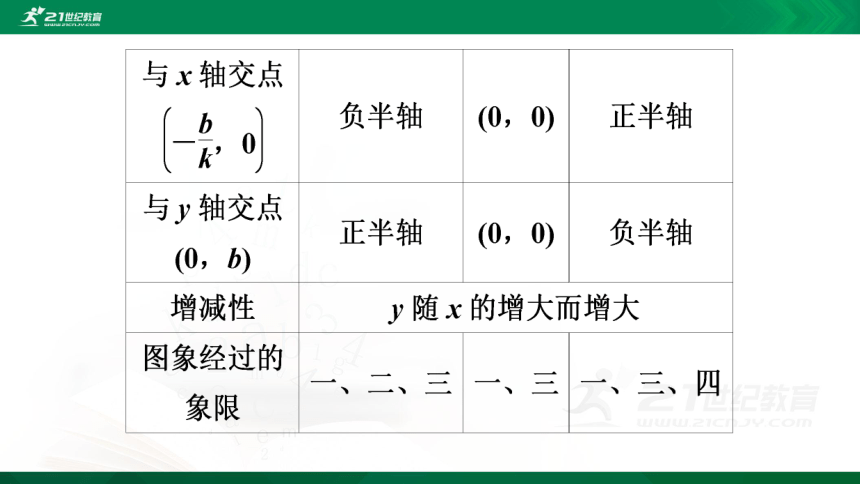
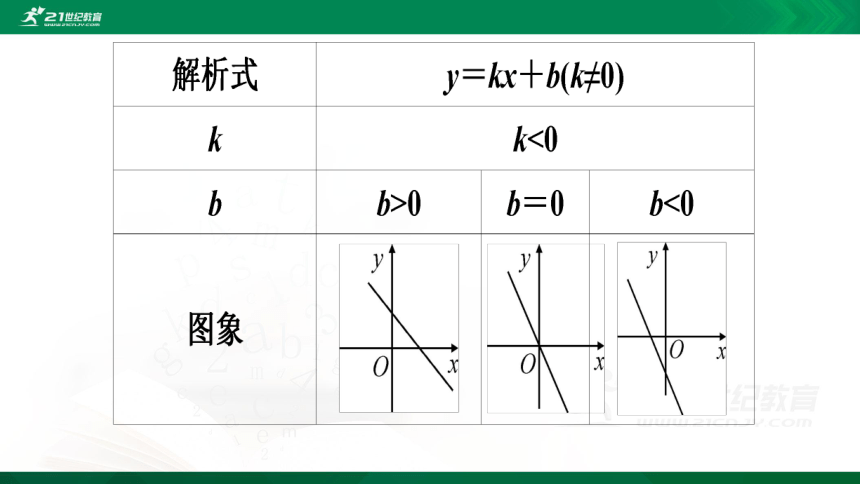
若两个变量x,y间的关系式可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数.
若两个变量x,y间的关系式可以表示成y=kx(k为常数,k≠0)的形式,则称y是x的正比例函数.
经过一点和原点便可画出正比例函数图象
经过二点便可画出一次函数图象
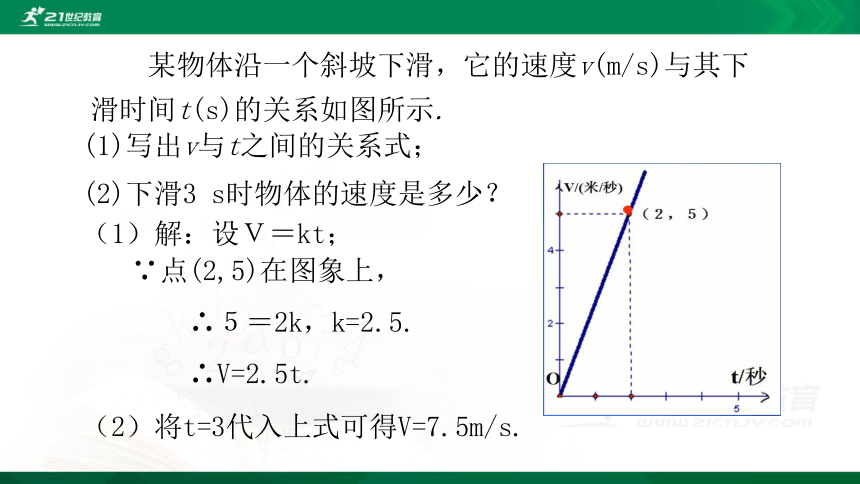
某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)的关系如图所示.
(1)写出v与t之间的关系式;
(2)下滑3
s时物体的速度是多少?
(1)解:设V=kt;
∵点(2,5)在图象上,
∴5=2k,k=2.5.
∴V=2.5t.
(2)将t=3代入上式可得V=7.5m/s.
确定正比例函数的表达式需要几个条件?确定一次函数的表达式呢?
确定正比例函数y=kx的表达式只需一个条件:除原点外的一点坐标或x、y的一组对应值.
由y=kx+b(k≠0)可知,一次函数含有两个基本量k和b,所以确定一次函数表达式一般需要两个条件:图象上两点坐标或自变量x和函数值y的两对对应值.
在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数。某弹簧不挂物体时长14.5
cm;当所挂物体的质量为3
kg时,弹簧长16
cm。写出y与x之间的关系式,并求当所挂物体的质量为4
kg时弹簧的长度.
当x=4时,y=0.5×4+14.5=16.5.
即物体的质量为4
kg时,弹簧长度为16.5
cm.
解:设y=kx+b(k≠0),
根据题意,得14.5=b,①
16=3k+b。②
将①代入②,得k=0.5。
所以在弹性限度内,y=0.5x+14.5.
知识拓展
利用待定系数法确定一次函数的关系式,其步骤为:
二代:确定两对对应值或图象上两个点的坐标,
分别代入函数关系式,得到关于k,b的两
个方程;
一设:根据题意,先设出函数关系式为
y=kx+b(k≠0);
三解:求出k,b的值(暂时可以通过等量代换的
方式去求两个未知数);
四定:最后确定函数关系式.
1.图象经过点(1,2),且y的值随着x值的增大而减小的一次函数的表达式可能是(
)
A.y=-2x+4
B.y=2x+4
C.y=-3x+1
D.y=3x-1
2.如图所示,直线l的表达式是(
)
A.y=x+2
B.y=-2x+2
C.y=x-2
D.y=-x-2
A
A
课堂练习
D
y1<y2
确定一次函数表达式的方法:
由问题的实际意义直接确定出函数表达式的一般形式:
若为正比例函数,则设其表达式为y=kx(k≠0),代入一个除原点以外的点的坐标,求出k的值,即可确定函数表达式;
若为一般的一次函数,则设其表达式为y=kx+b(k≠0),代入两个点的坐标,求出k,b的值,从而确定一次函数的表达式.
20
作业布置:
习题4.5
1,2,3,4
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
八年级
4
一次函数的应用(第1课时)
4
一次函数的应用(1)
若两个变量x,y间的关系式可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数.
若两个变量x,y间的关系式可以表示成y=kx(k为常数,k≠0)的形式,则称y是x的正比例函数.
经过一点和原点便可画出正比例函数图象
经过二点便可画出一次函数图象
某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)的关系如图所示.
(1)写出v与t之间的关系式;
(2)下滑3
s时物体的速度是多少?
(1)解:设V=kt;
∵点(2,5)在图象上,
∴5=2k,k=2.5.
∴V=2.5t.
(2)将t=3代入上式可得V=7.5m/s.
确定正比例函数的表达式需要几个条件?确定一次函数的表达式呢?
确定正比例函数y=kx的表达式只需一个条件:除原点外的一点坐标或x、y的一组对应值.
由y=kx+b(k≠0)可知,一次函数含有两个基本量k和b,所以确定一次函数表达式一般需要两个条件:图象上两点坐标或自变量x和函数值y的两对对应值.
在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数。某弹簧不挂物体时长14.5
cm;当所挂物体的质量为3
kg时,弹簧长16
cm。写出y与x之间的关系式,并求当所挂物体的质量为4
kg时弹簧的长度.
当x=4时,y=0.5×4+14.5=16.5.
即物体的质量为4
kg时,弹簧长度为16.5
cm.
解:设y=kx+b(k≠0),
根据题意,得14.5=b,①
16=3k+b。②
将①代入②,得k=0.5。
所以在弹性限度内,y=0.5x+14.5.
知识拓展
利用待定系数法确定一次函数的关系式,其步骤为:
二代:确定两对对应值或图象上两个点的坐标,
分别代入函数关系式,得到关于k,b的两
个方程;
一设:根据题意,先设出函数关系式为
y=kx+b(k≠0);
三解:求出k,b的值(暂时可以通过等量代换的
方式去求两个未知数);
四定:最后确定函数关系式.
1.图象经过点(1,2),且y的值随着x值的增大而减小的一次函数的表达式可能是(
)
A.y=-2x+4
B.y=2x+4
C.y=-3x+1
D.y=3x-1
2.如图所示,直线l的表达式是(
)
A.y=x+2
B.y=-2x+2
C.y=x-2
D.y=-x-2
A
A
课堂练习
D
y1<y2
确定一次函数表达式的方法:
由问题的实际意义直接确定出函数表达式的一般形式:
若为正比例函数,则设其表达式为y=kx(k≠0),代入一个除原点以外的点的坐标,求出k的值,即可确定函数表达式;
若为一般的一次函数,则设其表达式为y=kx+b(k≠0),代入两个点的坐标,求出k,b的值,从而确定一次函数的表达式.
20
作业布置:
习题4.5
1,2,3,4
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
