人教版八年级数学下册 18.1平行四边形的性质和判定同步练习(word 版 含答案)
文档属性
| 名称 | 人教版八年级数学下册 18.1平行四边形的性质和判定同步练习(word 版 含答案) | 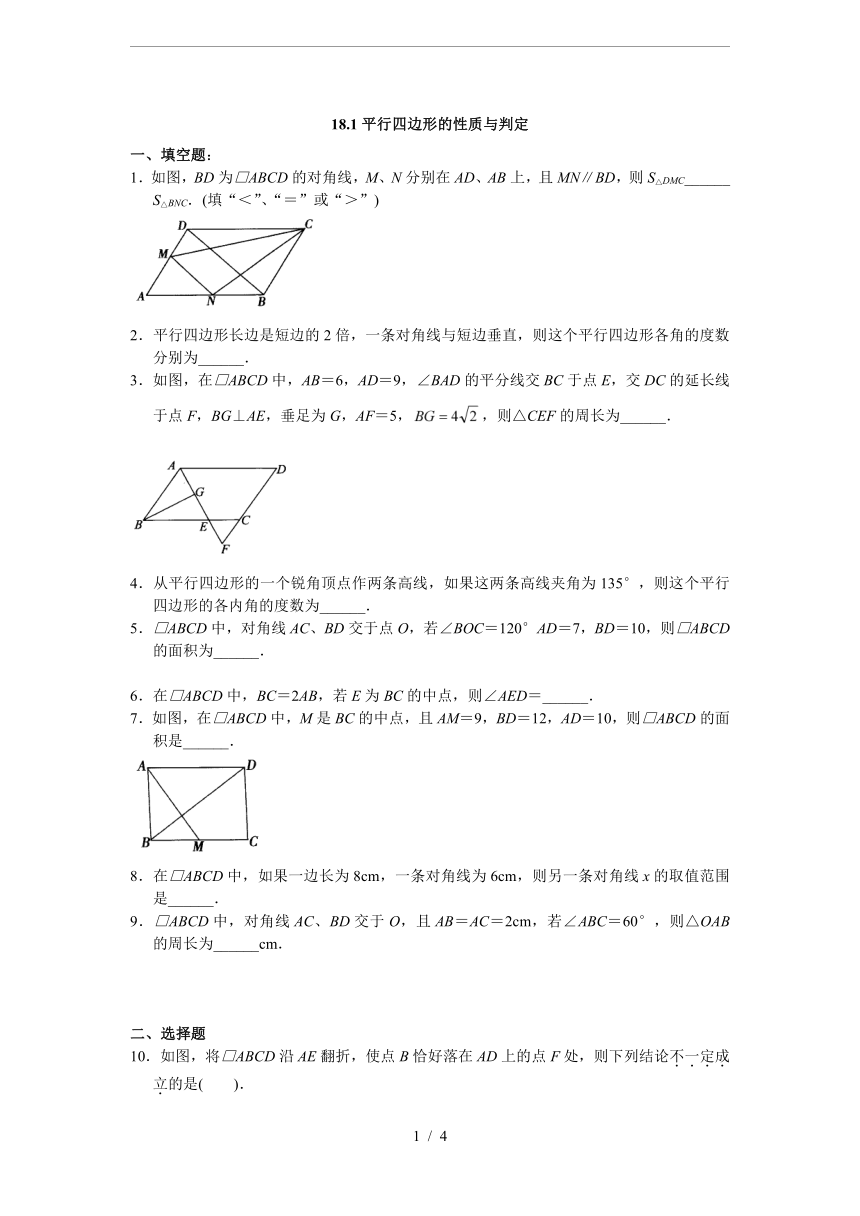 | |
| 格式 | zip | ||
| 文件大小 | 58.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 10:34:22 | ||
图片预览


文档简介
18.1平行四边形的性质与判定
一、填空题:
1.如图,BD为□ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC______
S△BNC.(填“<”、“=”或“>”)
2.平行四边形长边是短边的2倍,一条对角线与短边垂直,则这个平行四边形各角的度数分别为______.
3.如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AF=5,,则△CEF的周长为______.
4.从平行四边形的一个锐角顶点作两条高线,如果这两条高线夹角为135°,则这个平行四边形的各内角的度数为______.
5.□ABCD中,对角线AC、BD交于点O,若∠BOC=120°AD=7,BD=10,则□ABCD的面积为______.
6.在□ABCD中,BC=2AB,若E为BC的中点,则∠AED=______.
7.如图,在□ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则□ABCD的面积是______.
8.在□ABCD中,如果一边长为8cm,一条对角线为6cm,则另一条对角线x的取值范围是______.
9.□ABCD中,对角线AC、BD交于O,且AB=AC=2cm,若∠ABC=60°,则△OAB的周长为______cm.
二、选择题
10.如图,将□ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是(
).
(A)AF=EF
(B)AB=EF
(C)AE=AF
(D)AF=BE
11.如图,下列推理不正确的是(
).
(A)∵AB∥CD
∴∠ABC+∠C=180°
(B)∵∠1=∠2
∴AD∥BC
(C)∵AD∥BC
∴∠3=∠4
(D)∵∠A+∠ADC=180°
∴AB∥CD
12.下列命题中,正确的是(
).
(A)两组角相等的四边形是平行四边形
(B)一组对边相等,两条对角线相等的四边形是平行四边形
(C)一条对角线平分另一条对角线的四边形是平行四边形
(D)两组对边分别相等的四边形是平行四边形
13.已知:园边形ABCD中,AC与BD交于点O,如果只给出条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;
③如果再加上条件“OA=OC”,那么四边形ABCD一定是平行四边形;
④如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.其中正确的说法是(
).
(A)①②
(B)①③④
(C)②③
(D)②③④
14.能确定平行四边形的大小和形状的条件是(
).
(A)已知平行四边形的两邻边
(B)已知平行四边形的相邻两角
(C)已知平行四边形的两对角线
(D)已知平行四边形的一边、一对角线和周长
15.平行四边形两邻边分别为24和16,若两长边间的距离为8,则两短边间的距离为(
).
(A)5
(B)6
(C)8
(D)12
三、解答题
16.已知:如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB.AB=a,AD=b.
(1)求证:△EFC是等腰三角形;
(2)求EC+FC.
17.已知:如图,△ABC中,∠ABC=90°,BD⊥AC于D,AE平分∠BAC,EF∥DC,交BC于F.求证:BE=FC.
18.已知:如图,在□ABCD中,E为AD的中点,CE、BA的延长线交于点F.若BC=2CD,求证:∠F=∠BCF.
19.如图,已知:在□ABCD中,∠A=60°,E、F分别是AB、CD的中点,且AB=2AD.求证:BF∶BD=∶3.
答案
1.=.提示:连结BM,DN.
2.60°,120°,60°,120°.
3.7.
4.45°,135°,45°,135°.
5.
提示:作CE⊥BD于E,设OE=x,则BE2+CE2=BC2,得(x+5)2+.解出.S□=2S△BCD=BD×CE=
6.90°.
7.72.提示:作DE∥AM交BC延长线于E,作DF⊥BE于F,可得△BDE是直角三角形,
8.10cm<x<22cm.
9.
10.D.
11.C.
12.D.
13.C.
14.D.
15.C.
16.(1)提示:先证∠E=∠F;
(2)EC+FC=2a+2b.
17.提示:过E点作EM∥BC,交DC于M,证△AEB≌△AEM.
18.提示:先证DC=AF.
19.提示:连接DE,先证△ADE是等边三角形,进而证明∠ADB=90°,∠ABD=30°.
PAGE
/
NUMPAGES
一、填空题:
1.如图,BD为□ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC______
S△BNC.(填“<”、“=”或“>”)
2.平行四边形长边是短边的2倍,一条对角线与短边垂直,则这个平行四边形各角的度数分别为______.
3.如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AF=5,,则△CEF的周长为______.
4.从平行四边形的一个锐角顶点作两条高线,如果这两条高线夹角为135°,则这个平行四边形的各内角的度数为______.
5.□ABCD中,对角线AC、BD交于点O,若∠BOC=120°AD=7,BD=10,则□ABCD的面积为______.
6.在□ABCD中,BC=2AB,若E为BC的中点,则∠AED=______.
7.如图,在□ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则□ABCD的面积是______.
8.在□ABCD中,如果一边长为8cm,一条对角线为6cm,则另一条对角线x的取值范围是______.
9.□ABCD中,对角线AC、BD交于O,且AB=AC=2cm,若∠ABC=60°,则△OAB的周长为______cm.
二、选择题
10.如图,将□ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是(
).
(A)AF=EF
(B)AB=EF
(C)AE=AF
(D)AF=BE
11.如图,下列推理不正确的是(
).
(A)∵AB∥CD
∴∠ABC+∠C=180°
(B)∵∠1=∠2
∴AD∥BC
(C)∵AD∥BC
∴∠3=∠4
(D)∵∠A+∠ADC=180°
∴AB∥CD
12.下列命题中,正确的是(
).
(A)两组角相等的四边形是平行四边形
(B)一组对边相等,两条对角线相等的四边形是平行四边形
(C)一条对角线平分另一条对角线的四边形是平行四边形
(D)两组对边分别相等的四边形是平行四边形
13.已知:园边形ABCD中,AC与BD交于点O,如果只给出条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;
③如果再加上条件“OA=OC”,那么四边形ABCD一定是平行四边形;
④如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.其中正确的说法是(
).
(A)①②
(B)①③④
(C)②③
(D)②③④
14.能确定平行四边形的大小和形状的条件是(
).
(A)已知平行四边形的两邻边
(B)已知平行四边形的相邻两角
(C)已知平行四边形的两对角线
(D)已知平行四边形的一边、一对角线和周长
15.平行四边形两邻边分别为24和16,若两长边间的距离为8,则两短边间的距离为(
).
(A)5
(B)6
(C)8
(D)12
三、解答题
16.已知:如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB.AB=a,AD=b.
(1)求证:△EFC是等腰三角形;
(2)求EC+FC.
17.已知:如图,△ABC中,∠ABC=90°,BD⊥AC于D,AE平分∠BAC,EF∥DC,交BC于F.求证:BE=FC.
18.已知:如图,在□ABCD中,E为AD的中点,CE、BA的延长线交于点F.若BC=2CD,求证:∠F=∠BCF.
19.如图,已知:在□ABCD中,∠A=60°,E、F分别是AB、CD的中点,且AB=2AD.求证:BF∶BD=∶3.
答案
1.=.提示:连结BM,DN.
2.60°,120°,60°,120°.
3.7.
4.45°,135°,45°,135°.
5.
提示:作CE⊥BD于E,设OE=x,则BE2+CE2=BC2,得(x+5)2+.解出.S□=2S△BCD=BD×CE=
6.90°.
7.72.提示:作DE∥AM交BC延长线于E,作DF⊥BE于F,可得△BDE是直角三角形,
8.10cm<x<22cm.
9.
10.D.
11.C.
12.D.
13.C.
14.D.
15.C.
16.(1)提示:先证∠E=∠F;
(2)EC+FC=2a+2b.
17.提示:过E点作EM∥BC,交DC于M,证△AEB≌△AEM.
18.提示:先证DC=AF.
19.提示:连接DE,先证△ADE是等边三角形,进而证明∠ADB=90°,∠ABD=30°.
PAGE
/
NUMPAGES
