13.4 课题学习 最短路径问题同步练习题(含答案)
文档属性
| 名称 | 13.4 课题学习 最短路径问题同步练习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 17:21:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十三章 轴对称13.4 最短路径问题
练习
一、单选题(共10小题)
1.(2020·济南市期末)某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水. 某同学用直线(虛线)表示小河,两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( ).
A. B.
C. D.
2.(2019·余杭区期末)如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条公路连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A.B.
C.D.
3.(2020·泰安市期中)如图,直线l是一条河,A、B 是两个新农村定居点.欲在 l 上的某点处修建一个水泵站,由水泵站直接向 A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管 道最短的方案是( )
A. B.
C. D.
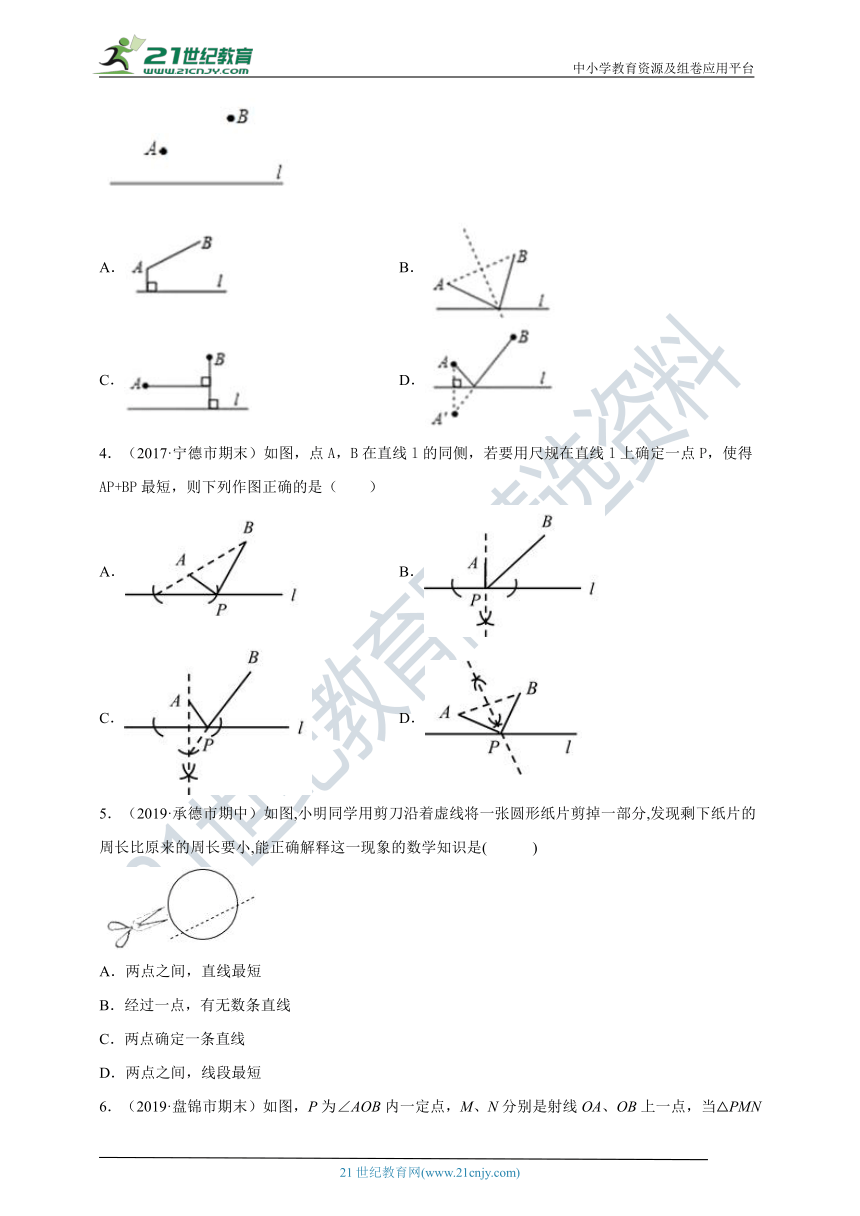
4.(2017·宁德市期末)如图,点A,B在直线l的同侧,若要用尺规在直线l上确定一点P,使得AP+BP最短,则下列作图正确的是( )
A. B.
C. D.
5.(2019·承德市期中)如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间,直线最短
B.经过一点,有无数条直线
C.两点确定一条直线
D.两点之间,线段最短
6.(2019·盘锦市期末)如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )
A.40° B.45° C.50° D.55°
7.(2019·商丘市期末)如图,点是内任意一点,且,点和点分别是射线和射线上的动点,当周长取最小值时,则的度数为( )
A.145° B.110° C.100° D.70°
8.(2020·丰台区期末)如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PB的最小值是( )
A.3 B.4 C.5 D.6
9.(2018·安庆市期末)如图,∠MON=45°,P为∠MON内一点,A为OM上一点,B为ON上一点,当PAB的周长取最小值时,∠APB的度数为( )
A.80° B.90° C.110° D.120°
10.(2020·杭州市期末)如图,A是直线l外一点,点B,E,D,C在直线l上,且,D为垂足,如果量得,,,,则点A到直线l的距离为( )
A.11 cm B.7 cm C.6 cm D.5 cm
二、解答题(共7小题)
11.(2019·庆阳市期中)下图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?(不写做法,保留作图痕迹)
12.(2018·腾冲市期末)作图题(保留作图痕迹,不写作法)
如图,A、B两村在一条小河MN的同一侧,要在河边建一水厂向两村供水.
(1)若要使自来水厂到两村的距离相等,在图1中用尺规作图作出厂址P的位置.
(2)若要使自来水厂到两村的输水管用料最省,在图2中作出厂址Q的位置.
13.如图所示,已知点是锐角内一点,试分别在上确定两点,使三角形的周长最小,写出你作图的主要步骤并标明你确定的点.
14.如图所示,P,Q为△ABC边上的两个定点,在BC上求作一点R,使△PQR的周长最小.
15.(2018·威海市期末)尺规作图:(不要求写作法,只保留作图痕迹)
如图,工厂A和工厂B,位于两条公路OC、OD之间的地带,现要建一座货物中转站P.若要求中转站P到两条公路OC、OD的距离相等,且到工厂A和工厂B的距离之和最短,请用尺规作出P的位置.
16.在旷野上,一个人骑马从A处出发,他先到河边N饮水,再到草场M出放马,然后返回A地,如图,请问他应该怎样走才能使总路程最短?
17.如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q、R(均不同于点O)则△PQR的周长的最小值是_____.
答案
一、单选题(共10小题)
1.C.2.C.3.D4.C5.D6.A7.B8.B9.B10.D
二、解答题(共7小题)
11.【答案】见解析【详解】试题解析:作点A关于燃气管道的对称点A′,连接A′B交燃气管道于点P,即点P即为所求.
12.【答案】作图见解析.【解析】
试题解析:(1)如图所示:点P即为所求;
(2)如图所示:点Q即为所求.
13.【答案】见详解.【详解】
作法:(1)分别作点A关于射线OM、ON的对称点P、Q,
(2)连结PQ,分别交OM、ON于点B、C.
则B、C就是所要求的点.
14.【答案】见解析试题解析:(1)作点P关于BC所在直线的对称点P′,
(2)连接P′Q,交BC于点R,则点R就是所求作的点(如图所示).
15.【答案】详见解析.【详解】
解:如图所示:点P即为所求.
16.【答案】见解析.【解析】
试题分析:先分别作出点关于两直线的对称点,连接交两直线于 则就是所求路径.试题解析:如图:
作点关于的对称点 作点关于的对称点,
连接分别交于点 连接
此人走路线,才能使总路程最短.
17.【答案】10【解析】试题解析:
作点关的对称点 连接,分别交与则即为所求的点.此时的周长最小.因为的周长就是的长(两点之间线段最短).
由图可知
所以是等边三角形.则 即的周长最小是
_21?????????è?????(www.21cnjy.com)_
第十三章 轴对称13.4 最短路径问题
练习
一、单选题(共10小题)
1.(2020·济南市期末)某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水. 某同学用直线(虛线)表示小河,两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( ).
A. B.
C. D.
2.(2019·余杭区期末)如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条公路连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A.B.
C.D.
3.(2020·泰安市期中)如图,直线l是一条河,A、B 是两个新农村定居点.欲在 l 上的某点处修建一个水泵站,由水泵站直接向 A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管 道最短的方案是( )
A. B.
C. D.
4.(2017·宁德市期末)如图,点A,B在直线l的同侧,若要用尺规在直线l上确定一点P,使得AP+BP最短,则下列作图正确的是( )
A. B.
C. D.
5.(2019·承德市期中)如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间,直线最短
B.经过一点,有无数条直线
C.两点确定一条直线
D.两点之间,线段最短
6.(2019·盘锦市期末)如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )
A.40° B.45° C.50° D.55°
7.(2019·商丘市期末)如图,点是内任意一点,且,点和点分别是射线和射线上的动点,当周长取最小值时,则的度数为( )
A.145° B.110° C.100° D.70°
8.(2020·丰台区期末)如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PB的最小值是( )
A.3 B.4 C.5 D.6
9.(2018·安庆市期末)如图,∠MON=45°,P为∠MON内一点,A为OM上一点,B为ON上一点,当PAB的周长取最小值时,∠APB的度数为( )
A.80° B.90° C.110° D.120°
10.(2020·杭州市期末)如图,A是直线l外一点,点B,E,D,C在直线l上,且,D为垂足,如果量得,,,,则点A到直线l的距离为( )
A.11 cm B.7 cm C.6 cm D.5 cm
二、解答题(共7小题)
11.(2019·庆阳市期中)下图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?(不写做法,保留作图痕迹)
12.(2018·腾冲市期末)作图题(保留作图痕迹,不写作法)
如图,A、B两村在一条小河MN的同一侧,要在河边建一水厂向两村供水.
(1)若要使自来水厂到两村的距离相等,在图1中用尺规作图作出厂址P的位置.
(2)若要使自来水厂到两村的输水管用料最省,在图2中作出厂址Q的位置.
13.如图所示,已知点是锐角内一点,试分别在上确定两点,使三角形的周长最小,写出你作图的主要步骤并标明你确定的点.
14.如图所示,P,Q为△ABC边上的两个定点,在BC上求作一点R,使△PQR的周长最小.
15.(2018·威海市期末)尺规作图:(不要求写作法,只保留作图痕迹)
如图,工厂A和工厂B,位于两条公路OC、OD之间的地带,现要建一座货物中转站P.若要求中转站P到两条公路OC、OD的距离相等,且到工厂A和工厂B的距离之和最短,请用尺规作出P的位置.
16.在旷野上,一个人骑马从A处出发,他先到河边N饮水,再到草场M出放马,然后返回A地,如图,请问他应该怎样走才能使总路程最短?
17.如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q、R(均不同于点O)则△PQR的周长的最小值是_____.
答案
一、单选题(共10小题)
1.C.2.C.3.D4.C5.D6.A7.B8.B9.B10.D
二、解答题(共7小题)
11.【答案】见解析【详解】试题解析:作点A关于燃气管道的对称点A′,连接A′B交燃气管道于点P,即点P即为所求.
12.【答案】作图见解析.【解析】
试题解析:(1)如图所示:点P即为所求;
(2)如图所示:点Q即为所求.
13.【答案】见详解.【详解】
作法:(1)分别作点A关于射线OM、ON的对称点P、Q,
(2)连结PQ,分别交OM、ON于点B、C.
则B、C就是所要求的点.
14.【答案】见解析试题解析:(1)作点P关于BC所在直线的对称点P′,
(2)连接P′Q,交BC于点R,则点R就是所求作的点(如图所示).
15.【答案】详见解析.【详解】
解:如图所示:点P即为所求.
16.【答案】见解析.【解析】
试题分析:先分别作出点关于两直线的对称点,连接交两直线于 则就是所求路径.试题解析:如图:
作点关于的对称点 作点关于的对称点,
连接分别交于点 连接
此人走路线,才能使总路程最短.
17.【答案】10【解析】试题解析:
作点关的对称点 连接,分别交与则即为所求的点.此时的周长最小.因为的周长就是的长(两点之间线段最短).
由图可知
所以是等边三角形.则 即的周长最小是
_21?????????è?????(www.21cnjy.com)_
