13.3 等腰三角形(第一课时 等腰三角形的性质)同步练习题(含答案)
文档属性
| 名称 | 13.3 等腰三角形(第一课时 等腰三角形的性质)同步练习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 17:09:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十三章 轴对称
13.3 等腰三角形(第一课时 等腰三角形的性质)
练习
一、单选题(共10小题)
1.(2019·揭阳市期末)若实数m、n满足 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是 (?? )
A.12 B.10 C.8或10 D.6
2.(2020·信阳市期末)如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
3.(2020·呼伦贝尔市期末)如图,已知在△ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
A.AE=EC B.AE=BE
C.∠EBC=∠BAC D.∠EBC=∠ABE
4.(2020·宝鸡市期末)如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
5.(2020·驻马店市期末)已知x,y满足,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16 B.20
C.16 D.以上答案都不对
6.(2020·太仓市期中)等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A.12 B.15 C.12或15 D.18
7.(2020·成都市期末)如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )
A.30° B.35° C.40° D.45°
8.(2019·巴彦淖尔市期末)如图,ABC是等腰三角形,点O 是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形ABC的腰长为5,面积为12,则OE+OF的值为( )
A.4 B. C.15 D.8
9.(2019·南京市期中)“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒,组成,两根棒在点相连并可绕转动,点固定,,点,可在槽中滑动,若,则的度数是( )
A.60° B.65° C.75° D.80°
10.(2019·铜陵市期末)等腰三角形一腰上的高与另一腰的夹角为45°,则其顶角为( )
A.45° B.135° C.45°或67.5° D.45°或135°
二、填空题(共5小题)
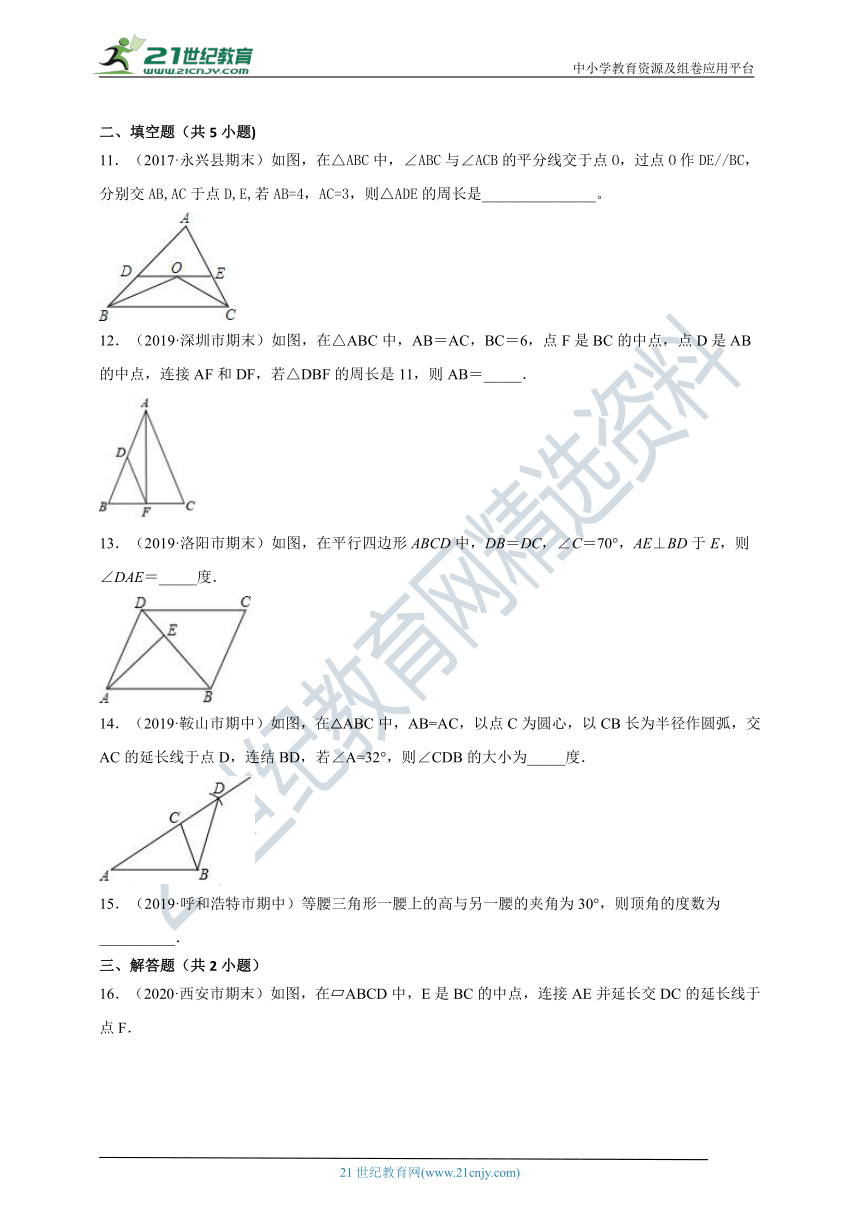
11.(2017·永兴县期末)如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE//BC,分别交AB,AC于点D,E,若AB=4,AC=3,则△ADE的周长是_______________。
12.(2019·深圳市期末)如图,在△ABC中,AB=AC,BC=6,点F是BC的中点,点D是AB的中点,连接AF和DF,若△DBF的周长是11,则AB=_____.
13.(2019·洛阳市期末)如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=_____度.
14.(2019·鞍山市期中)如图,在△ABC中,AB=AC,以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD,若∠A=32°,则∠CDB的大小为_____度.
15.(2019·呼和浩特市期中)等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为__________.
三、解答题(共2小题)
16.(2020·西安市期末)如图,在?ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
17.(2019·深圳市期末)如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.
(1)求证:AE=DE;
(2)若∠C=65°,求∠BDE的度数.
答案
一、单选题(共10小题)
1.B.2.B.3.C.4.A.5.B.6.B.7.C.8. B.9.D.10.D
二、填空题(共5小题)
11.【答案】7【解析】解:∵BO平分∠ABC,∴∠DBO=∠CBO,∵DE∥BC,
∴∠CBO=∠DOB,∴∠DBO=∠DOB,∴BD=DO,同理OE=EC,
∴△ADE的周长=AD+AE+ED=AB+AC=4+3=7.故答案为:7.
12.【答案】8【详解】解:∵AF⊥BC,BE⊥AC,D是AB的中点,
∴DE=DF=AB,∵AB=AC,AF⊥BC,
∴点F是BC的中点,∴BF=FC=3,∵BE⊥AC,
∴EF=BC=3,∴△DEF的周长=DE+DF+EF=AB+3=11,∴AB=8,故答案为8.
13.【答案】【详解】∵DB=DC,∠C=70°,∴∠DBC=∠C=70°,
在平行四边形ABCD中,∵AD∥BC,AE⊥BD,
∴∠ADB=∠DBC=∠C=70°,∠AED=90°,∴∠DAE=-70°=20°.故填空为:20°.
14.【答案】37【详解】∵AB=AC,∠A=32°,∴∠ABC=∠ACB=74°,
又∵BC=DC,∴∠CDB=∠CBD=∠ACB=37°,故答案为37.
15.【答案】60°或120°【详解】解:如图(1),∵AB=AC,BD⊥AC,∴∠ADB=90°,
∵∠ABD=30°,∴∠A=60°;如图(2),∵AB=AC,BD⊥AC,∴∠BDC=90°,∵∠ABD=30°,
∴∠BAD=60°,∴∠BAC=120°;综上所述,它的顶角度数为:60°或120°.
三、解答题(共2小题)
16.【答案】详见解析.【解析】(1)∵四边形ABCD是平行四边形,
∴AB∥DF,∴∠BAE=∠F,∵E是BC的中点,
∴BE=CE,在△AEB和△FEC中,
,
∴△AEB≌△FEC(AAS), ∴AB=CF;
(2)∵四边形ABCD是平行四边形,∴AB=CD,
∵AB=CF,DF=DC+CF ,∴DF=2CF,∴DF=2AB,
∵AD=2AB, ∴AD=DF,∵△AEB≌△FEC,∴AE=EF,∴ED⊥AF .
17.【答案】(1)证明见解析;(2)25°.【详解】证明:(1)∵DE∥BC,
∴∠C=∠ADE,∵AB=BC,∴∠C=∠A,∴∠A=∠ADE,∴AE=DE;
(2)∵△ABC中,AB=BC,∠C=65°,∴∠ABC=180°﹣65°﹣65°=50°,
∵AB=BC,D为AC中点,∴∠EBD=∠DBC=∠ABC=25°,
∵DE∥BC,∴∠BDE=∠DBC=25°.
_21?????????è?????(www.21cnjy.com)_
第十三章 轴对称
13.3 等腰三角形(第一课时 等腰三角形的性质)
练习
一、单选题(共10小题)
1.(2019·揭阳市期末)若实数m、n满足 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是 (?? )
A.12 B.10 C.8或10 D.6
2.(2020·信阳市期末)如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
3.(2020·呼伦贝尔市期末)如图,已知在△ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
A.AE=EC B.AE=BE
C.∠EBC=∠BAC D.∠EBC=∠ABE
4.(2020·宝鸡市期末)如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
5.(2020·驻马店市期末)已知x,y满足,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16 B.20
C.16 D.以上答案都不对
6.(2020·太仓市期中)等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A.12 B.15 C.12或15 D.18
7.(2020·成都市期末)如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )
A.30° B.35° C.40° D.45°
8.(2019·巴彦淖尔市期末)如图,ABC是等腰三角形,点O 是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形ABC的腰长为5,面积为12,则OE+OF的值为( )
A.4 B. C.15 D.8
9.(2019·南京市期中)“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒,组成,两根棒在点相连并可绕转动,点固定,,点,可在槽中滑动,若,则的度数是( )
A.60° B.65° C.75° D.80°
10.(2019·铜陵市期末)等腰三角形一腰上的高与另一腰的夹角为45°,则其顶角为( )
A.45° B.135° C.45°或67.5° D.45°或135°
二、填空题(共5小题)
11.(2017·永兴县期末)如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE//BC,分别交AB,AC于点D,E,若AB=4,AC=3,则△ADE的周长是_______________。
12.(2019·深圳市期末)如图,在△ABC中,AB=AC,BC=6,点F是BC的中点,点D是AB的中点,连接AF和DF,若△DBF的周长是11,则AB=_____.
13.(2019·洛阳市期末)如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=_____度.
14.(2019·鞍山市期中)如图,在△ABC中,AB=AC,以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD,若∠A=32°,则∠CDB的大小为_____度.
15.(2019·呼和浩特市期中)等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为__________.
三、解答题(共2小题)
16.(2020·西安市期末)如图,在?ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
17.(2019·深圳市期末)如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.
(1)求证:AE=DE;
(2)若∠C=65°,求∠BDE的度数.
答案
一、单选题(共10小题)
1.B.2.B.3.C.4.A.5.B.6.B.7.C.8. B.9.D.10.D
二、填空题(共5小题)
11.【答案】7【解析】解:∵BO平分∠ABC,∴∠DBO=∠CBO,∵DE∥BC,
∴∠CBO=∠DOB,∴∠DBO=∠DOB,∴BD=DO,同理OE=EC,
∴△ADE的周长=AD+AE+ED=AB+AC=4+3=7.故答案为:7.
12.【答案】8【详解】解:∵AF⊥BC,BE⊥AC,D是AB的中点,
∴DE=DF=AB,∵AB=AC,AF⊥BC,
∴点F是BC的中点,∴BF=FC=3,∵BE⊥AC,
∴EF=BC=3,∴△DEF的周长=DE+DF+EF=AB+3=11,∴AB=8,故答案为8.
13.【答案】【详解】∵DB=DC,∠C=70°,∴∠DBC=∠C=70°,
在平行四边形ABCD中,∵AD∥BC,AE⊥BD,
∴∠ADB=∠DBC=∠C=70°,∠AED=90°,∴∠DAE=-70°=20°.故填空为:20°.
14.【答案】37【详解】∵AB=AC,∠A=32°,∴∠ABC=∠ACB=74°,
又∵BC=DC,∴∠CDB=∠CBD=∠ACB=37°,故答案为37.
15.【答案】60°或120°【详解】解:如图(1),∵AB=AC,BD⊥AC,∴∠ADB=90°,
∵∠ABD=30°,∴∠A=60°;如图(2),∵AB=AC,BD⊥AC,∴∠BDC=90°,∵∠ABD=30°,
∴∠BAD=60°,∴∠BAC=120°;综上所述,它的顶角度数为:60°或120°.
三、解答题(共2小题)
16.【答案】详见解析.【解析】(1)∵四边形ABCD是平行四边形,
∴AB∥DF,∴∠BAE=∠F,∵E是BC的中点,
∴BE=CE,在△AEB和△FEC中,
,
∴△AEB≌△FEC(AAS), ∴AB=CF;
(2)∵四边形ABCD是平行四边形,∴AB=CD,
∵AB=CF,DF=DC+CF ,∴DF=2CF,∴DF=2AB,
∵AD=2AB, ∴AD=DF,∵△AEB≌△FEC,∴AE=EF,∴ED⊥AF .
17.【答案】(1)证明见解析;(2)25°.【详解】证明:(1)∵DE∥BC,
∴∠C=∠ADE,∵AB=BC,∴∠C=∠A,∴∠A=∠ADE,∴AE=DE;
(2)∵△ABC中,AB=BC,∠C=65°,∴∠ABC=180°﹣65°﹣65°=50°,
∵AB=BC,D为AC中点,∴∠EBD=∠DBC=∠ABC=25°,
∵DE∥BC,∴∠BDE=∠DBC=25°.
_21?????????è?????(www.21cnjy.com)_
