2.6.1 应用一元二次方程 课件(共15张PPT)
文档属性
| 名称 | 2.6.1 应用一元二次方程 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 20:27:47 | ||
图片预览





文档简介
(共15张PPT)
数学北师大版
九年级
2.6 应用一元二次方程第1课时
还记得本章开始时梯子下滑的问题吗?
①在这个问题中,梯子顶端下滑1米时,梯子底端滑动的距离大于1米,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
解:(1)设梯子顶端下滑x米时,梯子底端滑动的距离与顶端下滑的距离相等.由题意得:
解得x1=0(不符合题意,舍去),x2=2,
所以梯子顶端下滑2米时,梯子底端滑动的距离
与顶端下滑的距离相等.
②如果梯子长度是13米,梯子顶端与地面的垂直距离为12米,梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
解:(2)假设设梯子顶端下滑x米时,梯子底端滑动的距离与顶端下滑的距离相等.
解得x1=0(不符合题意,舍去),x2=7,
所以梯子顶端下滑7米时,梯子底端滑动的距离与顶端下滑的距离相等
例1
如图,某海军基地位于A处,在其正南方向200海里处有一目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
东
北
A
B
C
D
E
F
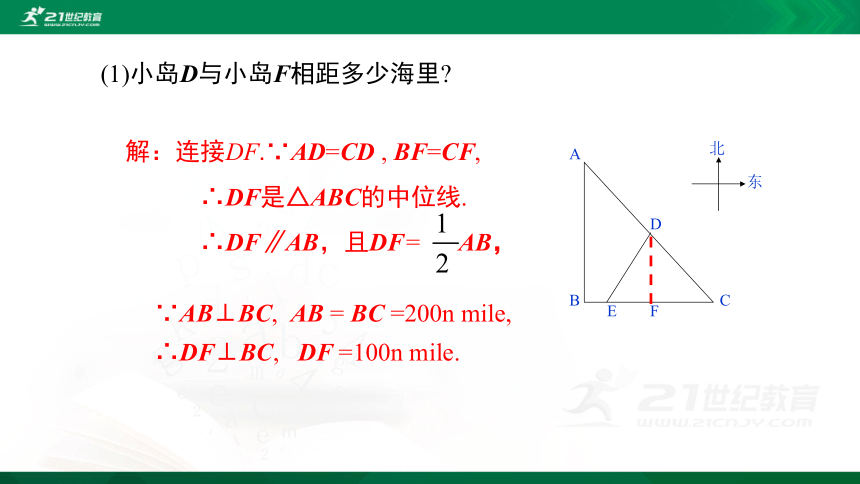
(1)小岛D与小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
(1)小岛D与小岛F相距多少海里?
东
北
A
B
C
D
E
F
解:连接DF.∵AD=CD
,
BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF=
AB,
∵AB⊥BC,
AB
=
BC
=200n
mile,
∴DF⊥BC,
DF
=100n
mile.
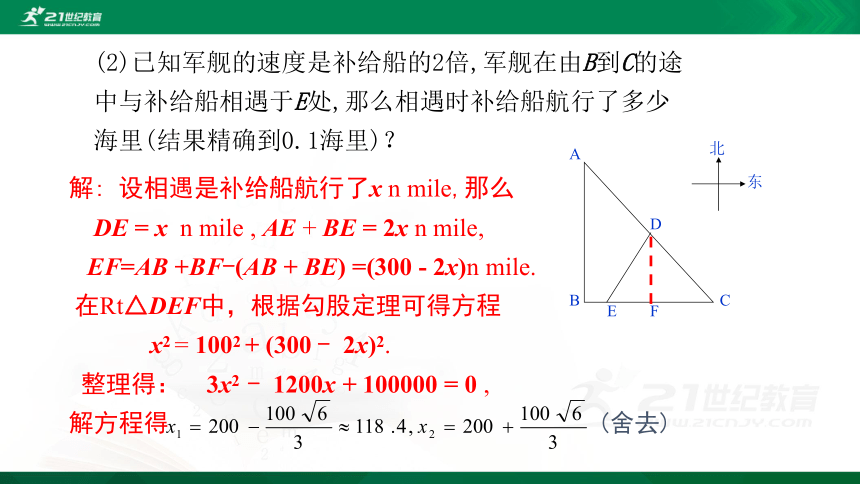
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?
东
北
A
B
C
D
E
F
解:
设相遇是补给船航行了x
n
mile,那么
DE
=
x
n
mile
,
AE
+
BE
=
2x
n
mile,
EF=AB
+BF-(AB
+
BE)
=(300
-
2x)n
mile.
在Rt△DEF中,根据勾股定理可得方程
x2
=
1002
+
(300
-
2x)2.
整理得:
3x2
-
1200x
+
100000
=
0
,
解方程得
(舍去)
练习:1.如图,在矩形ABCD中,AB=6cm,
BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?
A
D
B
C
P
(6
-
t)
2t
Q
解:设所需时间为
t
s,根据题意,得
2t
(6
-
t)
÷2
=
6×12
-
64.
整理得
t2
-
6t
+
8
=
0.
解方程,得
t1
=
2
,
t2
=
4
.
答:在第2秒和第4秒是五边形面积是
64cm2.
2.《九章算术》“勾股”章中有一题:“今有二人同所立.甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙各行几何?”
大意是说:已知甲,乙二人同时从同一地点出发,甲的速度是7,乙的速度是3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲,乙各走了多远?”
乙:3x
甲:
10
A
B
C
7x-10
解:设甲,乙相遇时所用时间为x,根据题意,得
(7x-10)2=(3x)2
+102.
整理得:2x2-7x=0.
解这个方程,得
∴x1=3.5,
x2=0(不合题意,舍去).
∴3x=3×3.5=10.5,
7x=7×3.5=24.5.
答:甲走了24.5步,乙走了10.5步.
3.如图,在Rt△ACB中,∠C=90°,AC=30
cm,BC=21
cm,动点P从点C出发,沿CA方向运动,动点Q同时从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1
cm/s.那么运动几秒时,它们相距15
cm?
设运动x秒时,它们相距15
cm,根据题意表示出CP,CQ的长,再根据勾股定理列出方程求解.
解:设运动x秒时,它们相距15
cm,
则CP=x
cm,则CQ=(21-x)cm,
依题意有x2+(21-x)2=152,
解得x1=9,x2=12.
故运动9秒或12秒时,它们相距15
cm.
作业布置:
习题2.9
1,2,3,4
选讲内容:
例2
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,试求甲种药品成本的年平均下降率是多少?
解:设甲种药品的年平均下降率为x.根据题意,列方程,得
5
000
(
1-x
)2
=
3000,
解方程,得
x1≈0.225,x2≈1.775.
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
例3
某公司去年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
解:设这个增长率为x.根据题意,得
200+200(1+x)
+200(1+x)2=950
整理方程,得
4x2+12x-7=0,
解这个方程得
x1=-3.5(舍去),x2=0.5.
答:这个增长率为50%.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
九年级
2.6 应用一元二次方程第1课时
还记得本章开始时梯子下滑的问题吗?
①在这个问题中,梯子顶端下滑1米时,梯子底端滑动的距离大于1米,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
解:(1)设梯子顶端下滑x米时,梯子底端滑动的距离与顶端下滑的距离相等.由题意得:
解得x1=0(不符合题意,舍去),x2=2,
所以梯子顶端下滑2米时,梯子底端滑动的距离
与顶端下滑的距离相等.
②如果梯子长度是13米,梯子顶端与地面的垂直距离为12米,梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
解:(2)假设设梯子顶端下滑x米时,梯子底端滑动的距离与顶端下滑的距离相等.
解得x1=0(不符合题意,舍去),x2=7,
所以梯子顶端下滑7米时,梯子底端滑动的距离与顶端下滑的距离相等
例1
如图,某海军基地位于A处,在其正南方向200海里处有一目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
东
北
A
B
C
D
E
F
(1)小岛D与小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
(1)小岛D与小岛F相距多少海里?
东
北
A
B
C
D
E
F
解:连接DF.∵AD=CD
,
BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF=
AB,
∵AB⊥BC,
AB
=
BC
=200n
mile,
∴DF⊥BC,
DF
=100n
mile.
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?
东
北
A
B
C
D
E
F
解:
设相遇是补给船航行了x
n
mile,那么
DE
=
x
n
mile
,
AE
+
BE
=
2x
n
mile,
EF=AB
+BF-(AB
+
BE)
=(300
-
2x)n
mile.
在Rt△DEF中,根据勾股定理可得方程
x2
=
1002
+
(300
-
2x)2.
整理得:
3x2
-
1200x
+
100000
=
0
,
解方程得
(舍去)
练习:1.如图,在矩形ABCD中,AB=6cm,
BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?
A
D
B
C
P
(6
-
t)
2t
Q
解:设所需时间为
t
s,根据题意,得
2t
(6
-
t)
÷2
=
6×12
-
64.
整理得
t2
-
6t
+
8
=
0.
解方程,得
t1
=
2
,
t2
=
4
.
答:在第2秒和第4秒是五边形面积是
64cm2.
2.《九章算术》“勾股”章中有一题:“今有二人同所立.甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙各行几何?”
大意是说:已知甲,乙二人同时从同一地点出发,甲的速度是7,乙的速度是3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲,乙各走了多远?”
乙:3x
甲:
10
A
B
C
7x-10
解:设甲,乙相遇时所用时间为x,根据题意,得
(7x-10)2=(3x)2
+102.
整理得:2x2-7x=0.
解这个方程,得
∴x1=3.5,
x2=0(不合题意,舍去).
∴3x=3×3.5=10.5,
7x=7×3.5=24.5.
答:甲走了24.5步,乙走了10.5步.
3.如图,在Rt△ACB中,∠C=90°,AC=30
cm,BC=21
cm,动点P从点C出发,沿CA方向运动,动点Q同时从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1
cm/s.那么运动几秒时,它们相距15
cm?
设运动x秒时,它们相距15
cm,根据题意表示出CP,CQ的长,再根据勾股定理列出方程求解.
解:设运动x秒时,它们相距15
cm,
则CP=x
cm,则CQ=(21-x)cm,
依题意有x2+(21-x)2=152,
解得x1=9,x2=12.
故运动9秒或12秒时,它们相距15
cm.
作业布置:
习题2.9
1,2,3,4
选讲内容:
例2
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,试求甲种药品成本的年平均下降率是多少?
解:设甲种药品的年平均下降率为x.根据题意,列方程,得
5
000
(
1-x
)2
=
3000,
解方程,得
x1≈0.225,x2≈1.775.
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
例3
某公司去年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
解:设这个增长率为x.根据题意,得
200+200(1+x)
+200(1+x)2=950
整理方程,得
4x2+12x-7=0,
解这个方程得
x1=-3.5(舍去),x2=0.5.
答:这个增长率为50%.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
