人教版八年级上数学13.3.1等腰三角形的性质与判定课件(共66张PPT)
文档属性
| 名称 | 人教版八年级上数学13.3.1等腰三角形的性质与判定课件(共66张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 08:18:45 | ||
图片预览





文档简介
例2.如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。
证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)
例3 已知:如图,∠A=90°,∠B=15°,BD=DC.
求证:AC= BD.
证明:
∵BD=DC,∠B=15°
∴∠DCB=∠B=15°(等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC= DC
∴AC= BD
例4.如图,已知△ABC中,AB=AC,BD=BC,AD=DE=EB.
求∠A的度数.
分析:本题有较多的等腰三角形的条件,最好用列方程组的方法来求解,应当在图形上标出各未知数,可使解题过程清晰明了。
例5.已知:如图,∠C=90°,BC=AC,D、E分别在BC和AC上,且BD=CE,M是AB的中点.
求证:△MDE是等腰三角形.
分析:要证△MDE是等腰三角形,只需证MD=ME。连结CM,可利用△BMD≌△CME得到结果。
例6.如图,在等边△ABC中,AF=BD=CE,
求证:△DEF也是等边三角形.
证明:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BD=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形
例7 如图2-8-1,中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G
求证:DG=EG
思路 因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。
例8 如图2-8-6,在△ABC中,AB=AC=CB,AE=CD,AD、BE相交于P,BQ⊥AD于Q.
求证:BP=2PQ
思路 在Rt△BPQ中,本题的结论等价于证明∠PBQ=30°
请把这个等腰三角形纸片折成两个等腰三角形!
例2.如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。
证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)
例3 已知:如图,∠A=90°,∠B=15°,BD=DC.
求证:AC= BD.
证明:
∵BD=DC,∠B=15°
∴∠DCB=∠B=15°(等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC= DC
∴AC= BD
例4.如图,已知△ABC中,AB=AC,BD=BC,AD=DE=EB.
求∠A的度数.
分析:本题有较多的等腰三角形的条件,最好用列方程组的方法来求解,应当在图形上标出各未知数,可使解题过程清晰明了。
例5.已知:如图,∠C=90°,BC=AC,D、E分别在BC和AC上,且BD=CE,M是AB的中点.
求证:△MDE是等腰三角形.
分析:要证△MDE是等腰三角形,只需证MD=ME。连结CM,可利用△BMD≌△CME得到结果。
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
等腰三角形的性质与判定
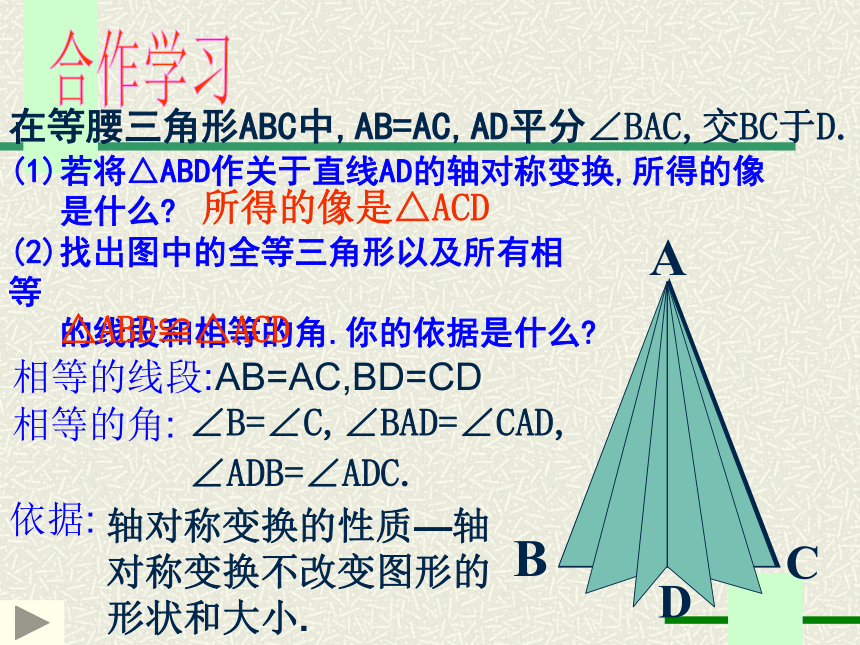
在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于D.
(1)若将△ABD作关于直线AD的轴对称变换,所得的像
是什么?
D
A
B
C
(2)找出图中的全等三角形以及所有相等
的线段和相等的角.你的依据是什么?
所得的像是△ACD
△ABD≌△ACD
相等的线段:
AB=AC,BD=CD
相等的角:
∠B=∠C,∠BAD=∠CAD,
∠ADB=∠ADC.
依据:
轴对称变换的性质—轴对称变换不改变图形的形状和大小.
1. ∠ B =∠ C
2. BD = CD, 即AD 为底边上的中线
3. AD⊥BC ,即AD为底边上的高
问题:由已知AB=AC得结论∠ B =∠ C用
文字如何表述?
等腰三角形的两个底角相等.
已知:AB=AC
A
D
C
B
可以说成 “在同一个三角形中,等边对等角”
结论:
,∠BAD=∠CAD(AD是顶角平分线).
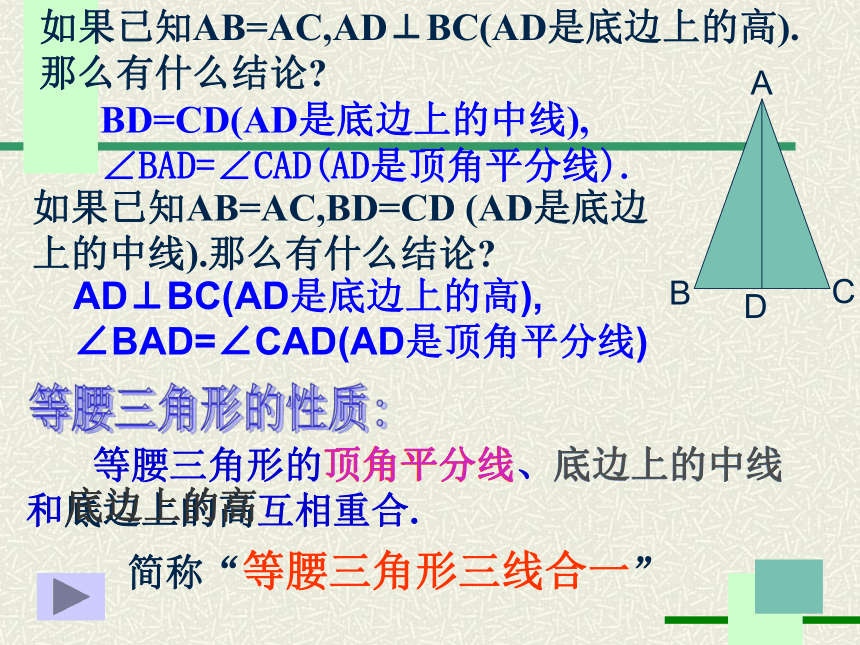
等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
简称“等腰三角形三线合一”
A
D
C
B
如果已知AB=AC,AD⊥BC(AD是底边上的高).
那么有什么结论?
如果已知AB=AC,BD=CD (AD是底边
上的中线).那么有什么结论?
顶角平分线
底边上的中线
底边上的高
BD=CD(AD是底边上的中线),
∠BAD=∠CAD(AD是顶角平分线).
AD⊥BC(AD是底边上的高),
∠BAD=∠CAD(AD是顶角平分线)
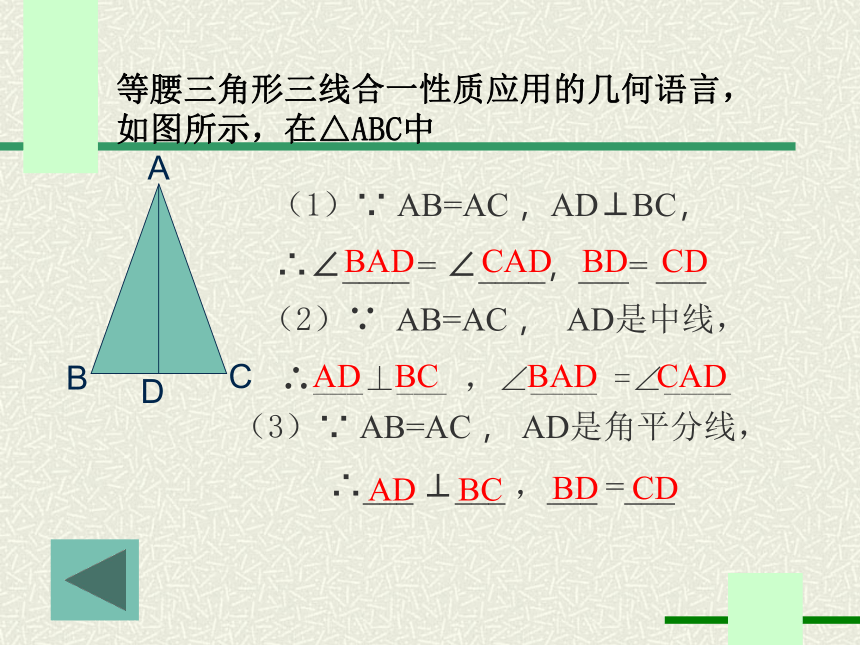
(1)∵ AB=AC ,AD⊥BC,
∴∠____ = ∠____,___= ___
(2)∵ AB=AC , AD是中线,
∴___⊥___ ,∠____ =∠____
(3)∵ AB=AC , AD是角平分线,
∴___ ⊥___ ,___ =___
BAD CAD
BD CD
AD BC
AD BC
BAD CAD
BD CD
等腰三角形三线合一性质应用的几何语言,如图所示,在△ABC中
A
D
C
B
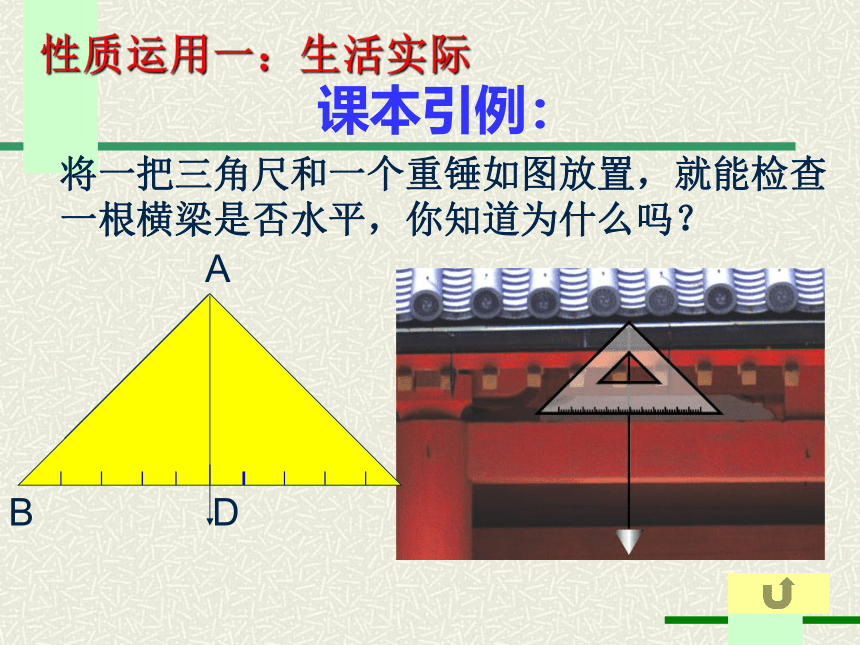
课本引例:
将一把三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道为什么吗?
D
A
B
性质运用一:生活实际
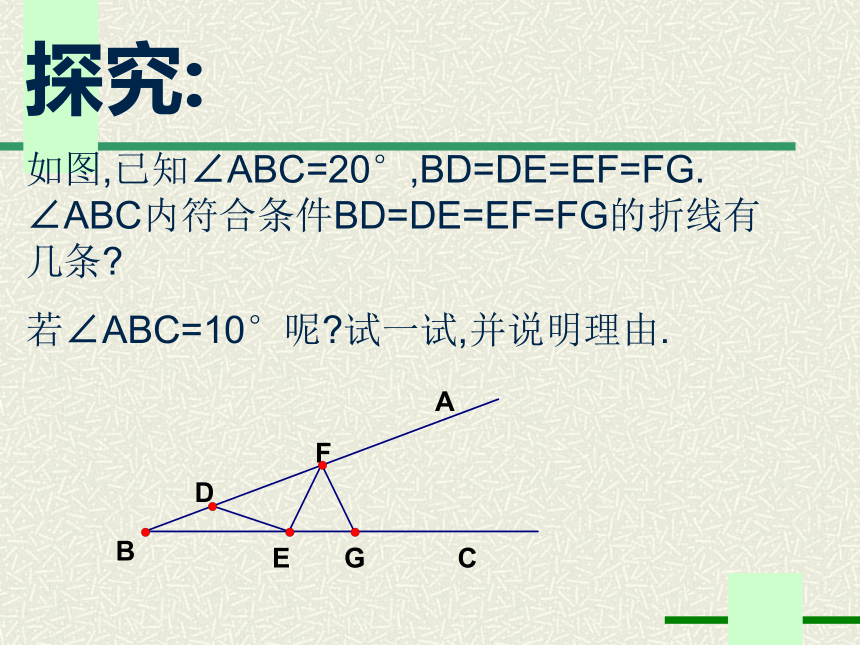
探究:
如图,已知∠ABC=20°,BD=DE=EF=FG. ∠ABC内符合条件BD=DE=EF=FG的折线有几条?
若∠ABC=10°呢?试一试,并说明理由.
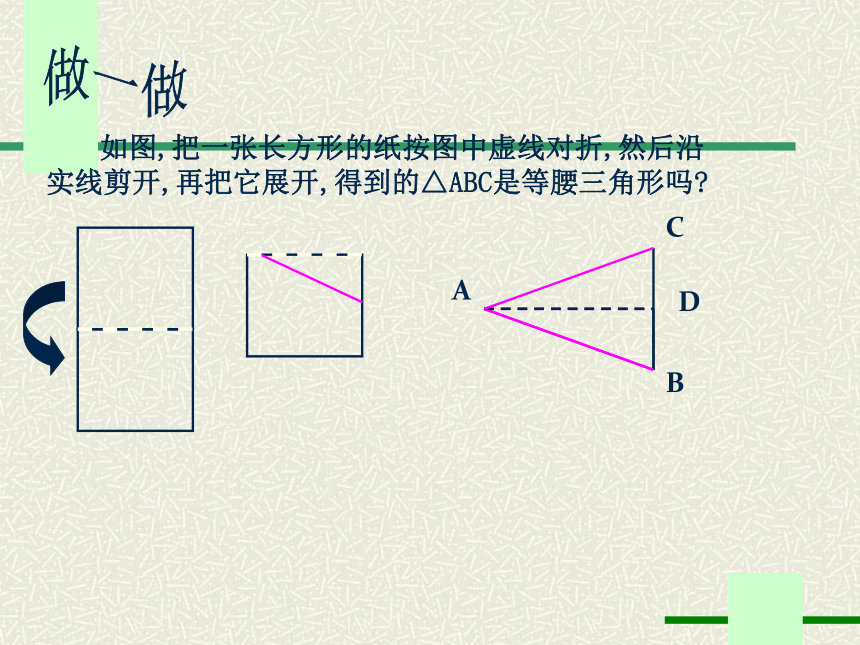
如图,把一张长方形的纸按图中虚线对折,然后沿
实线剪开,再把它展开,得到的△ABC是等腰三角形吗?
A
C
B
D
A
B
C
(3)
E
F
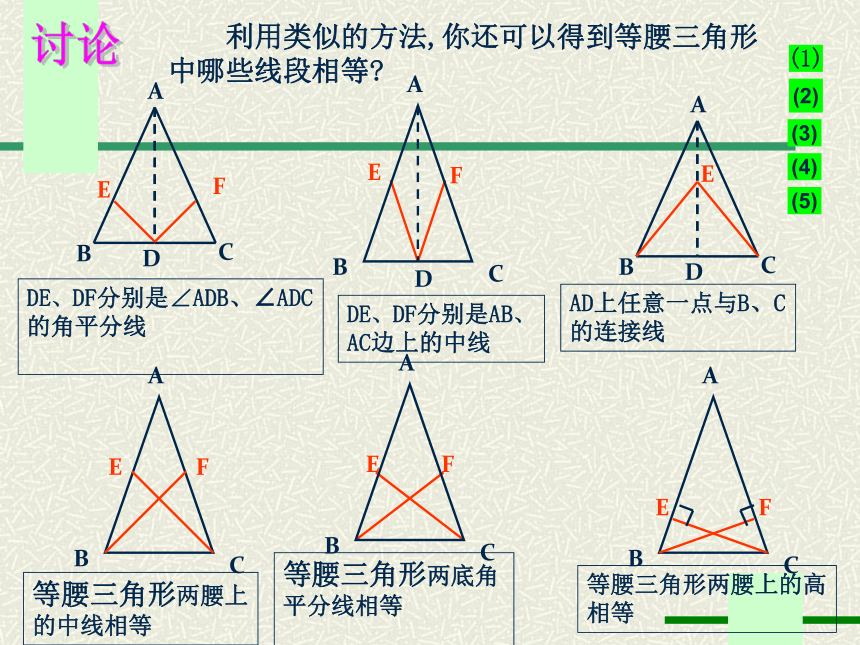
等腰三角形两腰上
的中线相等
A
B
C
(4)
E
F
等腰三角形两底角
平分线相等
A
B
C
(5)
E
F
等腰三角形两腰上的高
相等
利用类似的方法,你还可以得到等腰三角形
中哪些线段相等?
A
B
C
E
F
DE、DF分别是AB、
AC边上的中线
D
A
B
D
C
DE、DF分别是∠ADB、∠ADC
的角平分线
E
F
(1)
A
B
D
C
E
AD上任意一点与B、C
的连接线
(2)
⒈等腰三角形一个底角为70°,它的顶角为______.
⒉等腰三角形一个角为70°,它的另外两个角为
__________________.
⒊等腰三角形一个角为110°,它的另外两个角为___________.
① 顶角+2×底角=180°
② 顶角=180°-2×底角
③ 底角=(180°-顶角)÷2
④0°<顶角<180°
⑤0°<底角<90°
结论:在等腰三角形中,
40 °
35 °,35 °
70°,40°或55°,55°
例
如图,在△ABC中,AB=AC,D是BC边上的中点, ∠B=30°,求∠1和∠ADC的度数.
A
B
C
·
·
D
1
2
另解:
因为等腰三角形的“三线合一”,所以AD是△ABC的顶角平分线、底边上的高,即
∠1= ∠2, ∠ADC=90°
因为∠BAC=180°- 30°- 30°=
120°
所以 ∠1=
2
∠BAC
=
120°
2
=60°.
答: ∠1为60°, ∠ADC为90°.
·
30°
∟
等腰三角形的腰长等于9,另一边长等于4,
那么周长=___________.
2. 等腰三角形的腰长等于另一边的2倍,周长为30,
那么它的各边长分别为_____________.
3. 等腰三角形的一边长比腰长多2cm,周长等于29cm,
则三边长分别为_________________.
填空题:
22
12,12,6.
9,9,11.
4. 正三角形的边长等于8,则周长等于_____________.
5. 等边三角形的周长等于72cm,则边长=______________.
6. 等腰三角形若两边长为3和7,则其周长为___________.
7. 在等腰三角形中,一个内角为30°,则另外两个内角为
______________.
填空题:
24
24
17
75°, 75°或
或30°,120°
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
3、这个命题正确吗?你能证明吗?
自学指导:
阅读课本P73—74内容,思考并回答下列问题:
等腰三角形的判定定理 与性质定理有何不同?
等腰三角形判定定理与性质定理的证明思路是否一样?
两个推论 是怎样得到的?你有什么新的发现吗?
8分钟后,比谁能回答以上问题,并能做与例题 类似的练习。
已知:⊿ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
推论1证明
已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?
推论2证明
第一种情况:当顶角是600时。
第二种情况:当底角是600时。
已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BC
A
B
C
证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:AB=AC=BC
A
B
C
证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴AB=AC=BC
例1 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
如图,∠CAE是⊿ABC的外角,∠1=∠2,
AD∥BC。
求证:AB=AC
分析:
从求证看:要证AB=AC,需证∠B=∠C,
从已知看:因为∠1=∠2,AD∥BC
可以找出∠B,∠C与的关系。
已知:
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角)。
A
B
C
D
E
1
2
例3 在△ABC中,已知∠A=40°,
∠B=70°,判断△ABC是什么
三角形,为什么?
A
B
C
解:∵∠A+∠B+∠C=180°
(三角形内角和等于180°)
∴∠C=180°-∠A-∠B(等式的性质)
=180°-40°-70°=70°,
∴ ∠C=∠B.
∴ △ABC是等腰三角形.(等角对等边)
三、等腰三角形的识别方法(应用):
40°
70°
?
课本P99页“做一做”
四、特殊的等腰三角形
△ABC, △ACD, △BCD
45°
45°
45°
45°
△ABC是等腰直角三角形,∠ACB=90°,CD是底边上的高,那么图10.3.6中
共有哪几个等腰直角三角形?
同时标出图10.3.6所有
锐角的度数。
B
A
D
C
图10.3.6
等边
四、特殊的等腰三角形
1.三个角都是60°的三角形是等边
三角形吗?你能说明理由吗?
2.有两个角是60°的三角形是等边三角形吗?
3.有一个角是60°的等腰三角形是等边三角形吗?
B
A
C
有三个角相等的三角形是等边三角形。
思考:
结论:
(2) 三角形
P99页/练习3
1.如图,在等腰三角形△ABC中两底角的平分线BE和CD相交于O点,那么△OBC是什么三角形?为什么?
O
D
E
A
B
C
六、要做到熟练运用知识解决问题
O
D
E
A
B
C
解:
△OBC是等腰三角形.
∵BE平分∠ABC,CD平分∠ACB(已知)
又∵AD=AC(已知)
∴∠ABC= ∠ACB .(等边对等角)
∴∠OBC= ∠OCB
∴OB=OC (等角对等边)
∴△ABC是等腰三角形.
∴∠OBC= ∠ ABC , ∠OCB= ∠ACB
(角平分线定义),
则 ∠ABC= ∠ACB .
2.如图,在△ABC中,DE||BC,
∠A=70 °, ∠C=55°,则△ADE
是什么三角形?为什么?
B
D
E
C
A
六、要做到熟练运用知识解决问题
70 °
55 °
?
?
B
D
E
C
A
解
六、要做到熟练运用知识解决问题
2. 若等腰三角形的一个内角是45°,则它的顶角为90°( )
1.若等腰三角形两条边的长分别是5和8,则它的周长为 .
21或18
总结:在解等腰三角形的题目时,经常会运用
分类思想讨论,以防止掉入数学“陷阱”!
1、如果等腰三角形的一个外角为100°, 则这个等腰三角形的顶角为 。
2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。
A
B
C
D
说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。
解:设∠A=x ,∠EBD=y,∠C=z
∵AB=AC
∴∠ABC=∠C=z
∵BD=BC
∴∠C=∠BDC=z
∵BE=DE
∴∠EBD=∠EDB=90°
∵AD=DE
∴∠A=∠AED=x
又∵∠BDC=∠A+∠ABD,∠AED=∠EBD+∠EDB
(三角形的外角等于和它不相邻的两个内角的和)
∠A+∠ABC+∠ACB=180°(三角形内角和为180°)
∴解得x=45°
即:∠A=45°
证明:连结CM
∵∠C=90°,BC=AC
∴∠A=∠B=45°
∵M是AB的中点
∴CM平分∠BCA(等腰三角形顶角的平分线和底边上的中线重合)
∴∠MCE=∠MCB=∠BCA=45°
∴∠B=∠MCE=∠MCB
∴CM=MB(等角对等边)
在△BDE和△CEM中
∴△BDM≌△CEM(SAS)
∴MD=ME
∴△MDE是等腰三角形
说明:证明等边三角形有三种思路:
①证明三边相等 ②证明三角相等 ③证明三角形是有一个角为60°的等腰三角形。
具体问题中可利用不同的方式进行求解。
证明:过D作DH∥AE,交BC于H
∴
∵AB=AC ∴
∴
∴DB=DH
又∵DB=CE
∴DH=CE
又∵
∴
∴DG=EG.
说明 本题易明显得出DG和EG所在的△DBG和△ECG不全等,故要构造三角形的全等,本题的另一种证法是过E作EF∥BD,交BC的延长线于F,证明△DBG≌△EFG,同学们不妨试一试。
证明 ∵AB=CA,∠BAE=∠ACD=60°,AE=CD,
∴△BAE≌△ACD
∴∠ABE=∠CAD
∴∠BPQ=∠ABE+∠BAP
=∠CAD+∠BAP=60°
又∵BQ⊥AD
∴∠PBQ=30°
∴BP=2PQ
说明 本题把证明线段之间的关系转化为证明角的度数,这种转换问题的方法值得同学们细心体会。
B
C
A
B
C
A
E
D
在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E. C点在AB边上的落点为D,连结DE.
2. 若CE=1,则DE=_____.
3. 你还能找出哪些相等的线段吗?
4. 若AB=6,则△DEB的周长等于多少?
1. DE⊥AB吗?
1
1
DB=______.
即:CE=DE=DB
AD=AC=BC
C
A
B
O
C
A
E
F
O
B
等腰直角三角形ABC两底角的平分线AO与BO交于点O, 过O点作底边AB的平行线交AC于点F,交BC于点E. 则:
3. 若AC=10,则△CEF的周长为多少?
2. AF、FE、EB三条线段的长度有何关系?
1. 图中有几个等腰三角形?
AF+ EB=FE
相等角之间的转化
相等线段之间的转化
C
A
E
F
O
B
㈠
A
B
C
F
E
O
(二)
如图(二)当AC=12,BC=8.求△CFE的周长?
解:因为OA平分∠CAB.
所以∠FAO=∠OAB.
又因为EF∥AB.
所以∠FOA=∠OAB.
所以∠FAO=∠FOA
即:AF=OF
所以AC=AF+FC=OF+FC.
同理可得:BC=BE+EC=OE+EC.
所以△CFE的周长: =OF+FC+OE+EC
=AC+BC=12+8=20
如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?
O
D
150°
⌒
C
a
E
F
H
36°
⌒
A
B
C
B
C
⌒
A
D
36°
A
B
C
36°
⌒
D
请把这个三角形纸片折成两个等腰三角形!
⌒
⌒
⌒
20°
40°
120°
A
B
C
⌒
⌒
⌒
20°
40°
120°
C
A
B
D
⌒
⌒
⌒
20°
40°
120°
A
B
C
D
在下图三角形的边上找出一点,使得该点与
三角形的其中两顶点构成等腰三角形!
B
A
C
50°
110°
20°
1、对∠A进行讨论
2、对∠B进行讨论
3、对∠C进行讨论
C
A
B
A
C
B
20°
20°
20°
20°
C
A
B
50°
50°
C
A
B
80°
80°
20°
C
A
B
65°
65°
50°
C
A
B
35°
35°
110°
(分类讨论)
说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。
解:设∠A=x ,∠EBD=y,∠C=z
∵AB=AC
∴∠ABC=∠C=z
∵BD=BC
∴∠C=∠BDC=z
∵BE=DE
∴∠EBD=∠EDB=90°
∵AD=DE
∴∠A=∠AED=x
又∵∠BDC=∠A+∠ABD,∠AED=∠EBD+∠EDB
(三角形的外角等于和它不相邻的两个内角的和)
∠A+∠ABC+∠ACB=180°(三角形内角和为180°)
∴解得x=45°
即:∠A=45°
证明:连结CM
∵∠C=90°,BC=AC
∴∠A=∠B=45°
∵M是AB的中点
∴CM平分∠BCA(等腰三角形顶角的平分线和底边上的中线重合)
∴∠MCE=∠MCB=∠BCA=45°
∴∠B=∠MCE=∠MCB
∴CM=MB(等角对等边)
在△BDE和△CEM中
∴△BDM≌△CEM(SAS)
∴MD=ME
∴△MDE是等腰三角形
B
C
A
B
C
A
E
D
在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E. C点在AB边上的落点为D,连结DE.
2. 若CE=1,则DE=_____.
3. 你还能找出哪些相等的线段吗?
4. 若AB=6,则△DEB的周长等于多少?
1. DE⊥AB吗?
1
1
DB=______.
即:CE=DE=DB
AD=AC=BC
应用举例一
例1.在△ABC中,已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么?
答: △ABC是等腰三角形。
理由:
在△ABC中,
∵∠C=180°-∠A-∠B
(三角形内角和等于180°)
=180°-40°-70°
=70°
∴∠B=∠C=70°
∴AB=AC
(等角对等边)
即△ABC是等腰三角形
巩固练习一
口答:
1.在△ABC中,有两个内角分别是100°和40°,试判断△ABC是什么三角形?
2.“有两个底角相等的三角形是等腰三角形”,这句话对吗?
答:△ABC是等腰三角形。
答:这句话是错的。
因为在还没有判定是等腰三角形前不能讲“底角”。
巩固练习二
36°
36°
72°
1
2
72°
1
2
36°
72°
36°
△ABC,
△ABD,
△BDC
A
B
C
D
1.如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 中的等腰三角形有 。
图
巩固练习二
2.在等腰直角三角形ABC中, ∠ACB =90°,CD是底边上的高,那么图中有 个等腰直角三角形,分别是 。
A
B
C
D
45°
45°
45°
45°
△ACB、
△ADC、
△BDC
3
应用举例二
1
2
B
D
A
C
E
2
1
答:△ABC是等腰三角形。
理由:
∵AD平分∠EAC
∴∠1=∠2
(角平分线定义)
∵AD∥BC
∴∠1=∠B
(两直线平行,同位角相等)
∠2=∠C
(两直线平行,内错角相等)
∴∠B=∠C
∴AB=AC
(等角对等边)
即△ABC是等腰三角形。
例2.如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC,试判断△ABC的形状,并说明理由?
巩固练习三
答:△ABD是等腰三角形.
1
2
3
2
1.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?
A
B
D
C
理由:
∵BD平分∠ABC
∴∠1=∠2
(角平分线定义)
∵AD∥BC
∴∠2=∠3
(两直线平行,内错角相等)
∴∠1=∠3
∴AB=AD
(等角对等边)
即△ABD是等腰三角形.
巩固练习三
2.如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于点O,那么△OBC是什么三角形?为什么?
A
B
C
E
D
O
1
2
答:△OBC是等腰三角形。
理由:
∵△ABC中,AB=AC
∴∠ABC=∠ACB
(等边对等角)
∵BE平分∠ABC,CD平分∠ACB
∴∠1= ∠ABC,
∠2= ∠ACB,
(角平分线定义)
∴∠1=∠2
∴OB=OC
(等角对等边)
即△OBC是等腰三角形。
1.若等腰三角形二条边的长分别是4和8,则它的周长为______.
20
2.等腰三角形一个内角为80o ,则另外两个内角分别为_________ ____。
50°、50°或80°、20°
3.方程 的两个根是等腰三角形的底和腰,则这个三角形的周长为( )
A.12 B.12或15 C.15 D.不能确定
4.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A.30o B.40o C.45o D.36o
5.如图, ,请你添加一个条件: ,使 (只添一个即可).
D
O
C
B
A
第5题图
6.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
C
D
∠C= ∠D等
A
1.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A.(4,0) B.(1.0)
C.(-2 ,0) D.(2,0)
1
2
3
4
-1
1
2
x
y
A
0
2.在边长为4和6的矩形中作等腰三角形,使等腰三角形的一条边是矩形的长或宽,第三个顶点在矩形的边上,求所作三角形的面积.
(注:形状相同的三角形按一种计算.)
B
巩固训练:
D
A
B
C
例3 已知:AB=AC,BD平分∠ ABC,CD平分
∠ ACB,问:图中有几个等腰三角形?
△ ABC、 △ DBC
变式一:若过D作EF ∥ BC交AB于E,交AC于F,则图中又增加了几个等腰三角形?
增加了3个分别为
△ AEF、 △ EDB、 △ FDC
E
F
相等角之间的转化
开动脑筋 议一议:
EF= BE+CF
变式二:若将题中△ABC改为一般的三角形,其他条件不变,问:线段EF与线段BE,CF有何数量关系?
A
E D F
B C
相等线段之间的转化
变式三:若过△ABC的一个内角和一个外角平分线的交点作这两角的公共边的平行线,则线段EF与线段BE,CF有何数量关系?
EF= BE — CF
A
B
C
D
E
F
H
变式四:若过△ABC的两个外角平分线的交点作这两个角的公共边的平行线,则线段EF与线段AE,CF有何数量关系?
A
B
C
D
E
F
证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)
例3 已知:如图,∠A=90°,∠B=15°,BD=DC.
求证:AC= BD.
证明:
∵BD=DC,∠B=15°
∴∠DCB=∠B=15°(等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC= DC
∴AC= BD
例4.如图,已知△ABC中,AB=AC,BD=BC,AD=DE=EB.
求∠A的度数.
分析:本题有较多的等腰三角形的条件,最好用列方程组的方法来求解,应当在图形上标出各未知数,可使解题过程清晰明了。
例5.已知:如图,∠C=90°,BC=AC,D、E分别在BC和AC上,且BD=CE,M是AB的中点.
求证:△MDE是等腰三角形.
分析:要证△MDE是等腰三角形,只需证MD=ME。连结CM,可利用△BMD≌△CME得到结果。
例6.如图,在等边△ABC中,AF=BD=CE,
求证:△DEF也是等边三角形.
证明:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BD=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形
例7 如图2-8-1,中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G
求证:DG=EG
思路 因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。
例8 如图2-8-6,在△ABC中,AB=AC=CB,AE=CD,AD、BE相交于P,BQ⊥AD于Q.
求证:BP=2PQ
思路 在Rt△BPQ中,本题的结论等价于证明∠PBQ=30°
请把这个等腰三角形纸片折成两个等腰三角形!
例2.如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。
证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)
例3 已知:如图,∠A=90°,∠B=15°,BD=DC.
求证:AC= BD.
证明:
∵BD=DC,∠B=15°
∴∠DCB=∠B=15°(等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC= DC
∴AC= BD
例4.如图,已知△ABC中,AB=AC,BD=BC,AD=DE=EB.
求∠A的度数.
分析:本题有较多的等腰三角形的条件,最好用列方程组的方法来求解,应当在图形上标出各未知数,可使解题过程清晰明了。
例5.已知:如图,∠C=90°,BC=AC,D、E分别在BC和AC上,且BD=CE,M是AB的中点.
求证:△MDE是等腰三角形.
分析:要证△MDE是等腰三角形,只需证MD=ME。连结CM,可利用△BMD≌△CME得到结果。
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
等腰三角形的性质与判定
在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于D.
(1)若将△ABD作关于直线AD的轴对称变换,所得的像
是什么?
D
A
B
C
(2)找出图中的全等三角形以及所有相等
的线段和相等的角.你的依据是什么?
所得的像是△ACD
△ABD≌△ACD
相等的线段:
AB=AC,BD=CD
相等的角:
∠B=∠C,∠BAD=∠CAD,
∠ADB=∠ADC.
依据:
轴对称变换的性质—轴对称变换不改变图形的形状和大小.
1. ∠ B =∠ C
2. BD = CD, 即AD 为底边上的中线
3. AD⊥BC ,即AD为底边上的高
问题:由已知AB=AC得结论∠ B =∠ C用
文字如何表述?
等腰三角形的两个底角相等.
已知:AB=AC
A
D
C
B
可以说成 “在同一个三角形中,等边对等角”
结论:
,∠BAD=∠CAD(AD是顶角平分线).
等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
简称“等腰三角形三线合一”
A
D
C
B
如果已知AB=AC,AD⊥BC(AD是底边上的高).
那么有什么结论?
如果已知AB=AC,BD=CD (AD是底边
上的中线).那么有什么结论?
顶角平分线
底边上的中线
底边上的高
BD=CD(AD是底边上的中线),
∠BAD=∠CAD(AD是顶角平分线).
AD⊥BC(AD是底边上的高),
∠BAD=∠CAD(AD是顶角平分线)
(1)∵ AB=AC ,AD⊥BC,
∴∠____ = ∠____,___= ___
(2)∵ AB=AC , AD是中线,
∴___⊥___ ,∠____ =∠____
(3)∵ AB=AC , AD是角平分线,
∴___ ⊥___ ,___ =___
BAD CAD
BD CD
AD BC
AD BC
BAD CAD
BD CD
等腰三角形三线合一性质应用的几何语言,如图所示,在△ABC中
A
D
C
B
课本引例:
将一把三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道为什么吗?
D
A
B
性质运用一:生活实际
探究:
如图,已知∠ABC=20°,BD=DE=EF=FG. ∠ABC内符合条件BD=DE=EF=FG的折线有几条?
若∠ABC=10°呢?试一试,并说明理由.
如图,把一张长方形的纸按图中虚线对折,然后沿
实线剪开,再把它展开,得到的△ABC是等腰三角形吗?
A
C
B
D
A
B
C
(3)
E
F
等腰三角形两腰上
的中线相等
A
B
C
(4)
E
F
等腰三角形两底角
平分线相等
A
B
C
(5)
E
F
等腰三角形两腰上的高
相等
利用类似的方法,你还可以得到等腰三角形
中哪些线段相等?
A
B
C
E
F
DE、DF分别是AB、
AC边上的中线
D
A
B
D
C
DE、DF分别是∠ADB、∠ADC
的角平分线
E
F
(1)
A
B
D
C
E
AD上任意一点与B、C
的连接线
(2)
⒈等腰三角形一个底角为70°,它的顶角为______.
⒉等腰三角形一个角为70°,它的另外两个角为
__________________.
⒊等腰三角形一个角为110°,它的另外两个角为___________.
① 顶角+2×底角=180°
② 顶角=180°-2×底角
③ 底角=(180°-顶角)÷2
④0°<顶角<180°
⑤0°<底角<90°
结论:在等腰三角形中,
40 °
35 °,35 °
70°,40°或55°,55°
例
如图,在△ABC中,AB=AC,D是BC边上的中点, ∠B=30°,求∠1和∠ADC的度数.
A
B
C
·
·
D
1
2
另解:
因为等腰三角形的“三线合一”,所以AD是△ABC的顶角平分线、底边上的高,即
∠1= ∠2, ∠ADC=90°
因为∠BAC=180°- 30°- 30°=
120°
所以 ∠1=
2
∠BAC
=
120°
2
=60°.
答: ∠1为60°, ∠ADC为90°.
·
30°
∟
等腰三角形的腰长等于9,另一边长等于4,
那么周长=___________.
2. 等腰三角形的腰长等于另一边的2倍,周长为30,
那么它的各边长分别为_____________.
3. 等腰三角形的一边长比腰长多2cm,周长等于29cm,
则三边长分别为_________________.
填空题:
22
12,12,6.
9,9,11.
4. 正三角形的边长等于8,则周长等于_____________.
5. 等边三角形的周长等于72cm,则边长=______________.
6. 等腰三角形若两边长为3和7,则其周长为___________.
7. 在等腰三角形中,一个内角为30°,则另外两个内角为
______________.
填空题:
24
24
17
75°, 75°或
或30°,120°
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
3、这个命题正确吗?你能证明吗?
自学指导:
阅读课本P73—74内容,思考并回答下列问题:
等腰三角形的判定定理 与性质定理有何不同?
等腰三角形判定定理与性质定理的证明思路是否一样?
两个推论 是怎样得到的?你有什么新的发现吗?
8分钟后,比谁能回答以上问题,并能做与例题 类似的练习。
已知:⊿ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在⊿BAD和⊿CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴ ⊿BAD≌ ⊿CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
推论1证明
已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?
推论2证明
第一种情况:当顶角是600时。
第二种情况:当底角是600时。
已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BC
A
B
C
证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:AB=AC=BC
A
B
C
证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴AB=AC=BC
例1 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
如图,∠CAE是⊿ABC的外角,∠1=∠2,
AD∥BC。
求证:AB=AC
分析:
从求证看:要证AB=AC,需证∠B=∠C,
从已知看:因为∠1=∠2,AD∥BC
可以找出∠B,∠C与的关系。
已知:
证明:
∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角)。
A
B
C
D
E
1
2
例3 在△ABC中,已知∠A=40°,
∠B=70°,判断△ABC是什么
三角形,为什么?
A
B
C
解:∵∠A+∠B+∠C=180°
(三角形内角和等于180°)
∴∠C=180°-∠A-∠B(等式的性质)
=180°-40°-70°=70°,
∴ ∠C=∠B.
∴ △ABC是等腰三角形.(等角对等边)
三、等腰三角形的识别方法(应用):
40°
70°
?
课本P99页“做一做”
四、特殊的等腰三角形
△ABC, △ACD, △BCD
45°
45°
45°
45°
△ABC是等腰直角三角形,∠ACB=90°,CD是底边上的高,那么图10.3.6中
共有哪几个等腰直角三角形?
同时标出图10.3.6所有
锐角的度数。
B
A
D
C
图10.3.6
等边
四、特殊的等腰三角形
1.三个角都是60°的三角形是等边
三角形吗?你能说明理由吗?
2.有两个角是60°的三角形是等边三角形吗?
3.有一个角是60°的等腰三角形是等边三角形吗?
B
A
C
有三个角相等的三角形是等边三角形。
思考:
结论:
(2) 三角形
P99页/练习3
1.如图,在等腰三角形△ABC中两底角的平分线BE和CD相交于O点,那么△OBC是什么三角形?为什么?
O
D
E
A
B
C
六、要做到熟练运用知识解决问题
O
D
E
A
B
C
解:
△OBC是等腰三角形.
∵BE平分∠ABC,CD平分∠ACB(已知)
又∵AD=AC(已知)
∴∠ABC= ∠ACB .(等边对等角)
∴∠OBC= ∠OCB
∴OB=OC (等角对等边)
∴△ABC是等腰三角形.
∴∠OBC= ∠ ABC , ∠OCB= ∠ACB
(角平分线定义),
则 ∠ABC= ∠ACB .
2.如图,在△ABC中,DE||BC,
∠A=70 °, ∠C=55°,则△ADE
是什么三角形?为什么?
B
D
E
C
A
六、要做到熟练运用知识解决问题
70 °
55 °
?
?
B
D
E
C
A
解
六、要做到熟练运用知识解决问题
2. 若等腰三角形的一个内角是45°,则它的顶角为90°( )
1.若等腰三角形两条边的长分别是5和8,则它的周长为 .
21或18
总结:在解等腰三角形的题目时,经常会运用
分类思想讨论,以防止掉入数学“陷阱”!
1、如果等腰三角形的一个外角为100°, 则这个等腰三角形的顶角为 。
2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。
A
B
C
D
说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。
解:设∠A=x ,∠EBD=y,∠C=z
∵AB=AC
∴∠ABC=∠C=z
∵BD=BC
∴∠C=∠BDC=z
∵BE=DE
∴∠EBD=∠EDB=90°
∵AD=DE
∴∠A=∠AED=x
又∵∠BDC=∠A+∠ABD,∠AED=∠EBD+∠EDB
(三角形的外角等于和它不相邻的两个内角的和)
∠A+∠ABC+∠ACB=180°(三角形内角和为180°)
∴解得x=45°
即:∠A=45°
证明:连结CM
∵∠C=90°,BC=AC
∴∠A=∠B=45°
∵M是AB的中点
∴CM平分∠BCA(等腰三角形顶角的平分线和底边上的中线重合)
∴∠MCE=∠MCB=∠BCA=45°
∴∠B=∠MCE=∠MCB
∴CM=MB(等角对等边)
在△BDE和△CEM中
∴△BDM≌△CEM(SAS)
∴MD=ME
∴△MDE是等腰三角形
说明:证明等边三角形有三种思路:
①证明三边相等 ②证明三角相等 ③证明三角形是有一个角为60°的等腰三角形。
具体问题中可利用不同的方式进行求解。
证明:过D作DH∥AE,交BC于H
∴
∵AB=AC ∴
∴
∴DB=DH
又∵DB=CE
∴DH=CE
又∵
∴
∴DG=EG.
说明 本题易明显得出DG和EG所在的△DBG和△ECG不全等,故要构造三角形的全等,本题的另一种证法是过E作EF∥BD,交BC的延长线于F,证明△DBG≌△EFG,同学们不妨试一试。
证明 ∵AB=CA,∠BAE=∠ACD=60°,AE=CD,
∴△BAE≌△ACD
∴∠ABE=∠CAD
∴∠BPQ=∠ABE+∠BAP
=∠CAD+∠BAP=60°
又∵BQ⊥AD
∴∠PBQ=30°
∴BP=2PQ
说明 本题把证明线段之间的关系转化为证明角的度数,这种转换问题的方法值得同学们细心体会。
B
C
A
B
C
A
E
D
在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E. C点在AB边上的落点为D,连结DE.
2. 若CE=1,则DE=_____.
3. 你还能找出哪些相等的线段吗?
4. 若AB=6,则△DEB的周长等于多少?
1. DE⊥AB吗?
1
1
DB=______.
即:CE=DE=DB
AD=AC=BC
C
A
B
O
C
A
E
F
O
B
等腰直角三角形ABC两底角的平分线AO与BO交于点O, 过O点作底边AB的平行线交AC于点F,交BC于点E. 则:
3. 若AC=10,则△CEF的周长为多少?
2. AF、FE、EB三条线段的长度有何关系?
1. 图中有几个等腰三角形?
AF+ EB=FE
相等角之间的转化
相等线段之间的转化
C
A
E
F
O
B
㈠
A
B
C
F
E
O
(二)
如图(二)当AC=12,BC=8.求△CFE的周长?
解:因为OA平分∠CAB.
所以∠FAO=∠OAB.
又因为EF∥AB.
所以∠FOA=∠OAB.
所以∠FAO=∠FOA
即:AF=OF
所以AC=AF+FC=OF+FC.
同理可得:BC=BE+EC=OE+EC.
所以△CFE的周长: =OF+FC+OE+EC
=AC+BC=12+8=20
如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?
O
D
150°
⌒
C
a
E
F
H
36°
⌒
A
B
C
B
C
⌒
A
D
36°
A
B
C
36°
⌒
D
请把这个三角形纸片折成两个等腰三角形!
⌒
⌒
⌒
20°
40°
120°
A
B
C
⌒
⌒
⌒
20°
40°
120°
C
A
B
D
⌒
⌒
⌒
20°
40°
120°
A
B
C
D
在下图三角形的边上找出一点,使得该点与
三角形的其中两顶点构成等腰三角形!
B
A
C
50°
110°
20°
1、对∠A进行讨论
2、对∠B进行讨论
3、对∠C进行讨论
C
A
B
A
C
B
20°
20°
20°
20°
C
A
B
50°
50°
C
A
B
80°
80°
20°
C
A
B
65°
65°
50°
C
A
B
35°
35°
110°
(分类讨论)
说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。
解:设∠A=x ,∠EBD=y,∠C=z
∵AB=AC
∴∠ABC=∠C=z
∵BD=BC
∴∠C=∠BDC=z
∵BE=DE
∴∠EBD=∠EDB=90°
∵AD=DE
∴∠A=∠AED=x
又∵∠BDC=∠A+∠ABD,∠AED=∠EBD+∠EDB
(三角形的外角等于和它不相邻的两个内角的和)
∠A+∠ABC+∠ACB=180°(三角形内角和为180°)
∴解得x=45°
即:∠A=45°
证明:连结CM
∵∠C=90°,BC=AC
∴∠A=∠B=45°
∵M是AB的中点
∴CM平分∠BCA(等腰三角形顶角的平分线和底边上的中线重合)
∴∠MCE=∠MCB=∠BCA=45°
∴∠B=∠MCE=∠MCB
∴CM=MB(等角对等边)
在△BDE和△CEM中
∴△BDM≌△CEM(SAS)
∴MD=ME
∴△MDE是等腰三角形
B
C
A
B
C
A
E
D
在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E. C点在AB边上的落点为D,连结DE.
2. 若CE=1,则DE=_____.
3. 你还能找出哪些相等的线段吗?
4. 若AB=6,则△DEB的周长等于多少?
1. DE⊥AB吗?
1
1
DB=______.
即:CE=DE=DB
AD=AC=BC
应用举例一
例1.在△ABC中,已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么?
答: △ABC是等腰三角形。
理由:
在△ABC中,
∵∠C=180°-∠A-∠B
(三角形内角和等于180°)
=180°-40°-70°
=70°
∴∠B=∠C=70°
∴AB=AC
(等角对等边)
即△ABC是等腰三角形
巩固练习一
口答:
1.在△ABC中,有两个内角分别是100°和40°,试判断△ABC是什么三角形?
2.“有两个底角相等的三角形是等腰三角形”,这句话对吗?
答:△ABC是等腰三角形。
答:这句话是错的。
因为在还没有判定是等腰三角形前不能讲“底角”。
巩固练习二
36°
36°
72°
1
2
72°
1
2
36°
72°
36°
△ABC,
△ABD,
△BDC
A
B
C
D
1.如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 中的等腰三角形有 。
图
巩固练习二
2.在等腰直角三角形ABC中, ∠ACB =90°,CD是底边上的高,那么图中有 个等腰直角三角形,分别是 。
A
B
C
D
45°
45°
45°
45°
△ACB、
△ADC、
△BDC
3
应用举例二
1
2
B
D
A
C
E
2
1
答:△ABC是等腰三角形。
理由:
∵AD平分∠EAC
∴∠1=∠2
(角平分线定义)
∵AD∥BC
∴∠1=∠B
(两直线平行,同位角相等)
∠2=∠C
(两直线平行,内错角相等)
∴∠B=∠C
∴AB=AC
(等角对等边)
即△ABC是等腰三角形。
例2.如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC,试判断△ABC的形状,并说明理由?
巩固练习三
答:△ABD是等腰三角形.
1
2
3
2
1.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?
A
B
D
C
理由:
∵BD平分∠ABC
∴∠1=∠2
(角平分线定义)
∵AD∥BC
∴∠2=∠3
(两直线平行,内错角相等)
∴∠1=∠3
∴AB=AD
(等角对等边)
即△ABD是等腰三角形.
巩固练习三
2.如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于点O,那么△OBC是什么三角形?为什么?
A
B
C
E
D
O
1
2
答:△OBC是等腰三角形。
理由:
∵△ABC中,AB=AC
∴∠ABC=∠ACB
(等边对等角)
∵BE平分∠ABC,CD平分∠ACB
∴∠1= ∠ABC,
∠2= ∠ACB,
(角平分线定义)
∴∠1=∠2
∴OB=OC
(等角对等边)
即△OBC是等腰三角形。
1.若等腰三角形二条边的长分别是4和8,则它的周长为______.
20
2.等腰三角形一个内角为80o ,则另外两个内角分别为_________ ____。
50°、50°或80°、20°
3.方程 的两个根是等腰三角形的底和腰,则这个三角形的周长为( )
A.12 B.12或15 C.15 D.不能确定
4.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A.30o B.40o C.45o D.36o
5.如图, ,请你添加一个条件: ,使 (只添一个即可).
D
O
C
B
A
第5题图
6.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
C
D
∠C= ∠D等
A
1.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A.(4,0) B.(1.0)
C.(-2 ,0) D.(2,0)
1
2
3
4
-1
1
2
x
y
A
0
2.在边长为4和6的矩形中作等腰三角形,使等腰三角形的一条边是矩形的长或宽,第三个顶点在矩形的边上,求所作三角形的面积.
(注:形状相同的三角形按一种计算.)
B
巩固训练:
D
A
B
C
例3 已知:AB=AC,BD平分∠ ABC,CD平分
∠ ACB,问:图中有几个等腰三角形?
△ ABC、 △ DBC
变式一:若过D作EF ∥ BC交AB于E,交AC于F,则图中又增加了几个等腰三角形?
增加了3个分别为
△ AEF、 △ EDB、 △ FDC
E
F
相等角之间的转化
开动脑筋 议一议:
EF= BE+CF
变式二:若将题中△ABC改为一般的三角形,其他条件不变,问:线段EF与线段BE,CF有何数量关系?
A
E D F
B C
相等线段之间的转化
变式三:若过△ABC的一个内角和一个外角平分线的交点作这两角的公共边的平行线,则线段EF与线段BE,CF有何数量关系?
EF= BE — CF
A
B
C
D
E
F
H
变式四:若过△ABC的两个外角平分线的交点作这两个角的公共边的平行线,则线段EF与线段AE,CF有何数量关系?
A
B
C
D
E
F
