冀教版数学七年级上5.4 第2课时 列一元一次方程解决相遇问题、工程问题 导学案(含答案)
文档属性
| 名称 | 冀教版数学七年级上5.4 第2课时 列一元一次方程解决相遇问题、工程问题 导学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 105.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 00:00:00 | ||
图片预览


文档简介
5.4
一元一次方程的应用
第2课时
列一元一次方程解决相遇问题、工程问题
学习目标:
1.掌握相遇问题、工程问题中的基本等量关系;
2.学会利用线段图分析相遇问题及工程问题,分清有关数量关系,正确找出作为列方程依据的主要等量关系;(难点)
3.进一步掌握用一元一次方程解决实际问题的基本过程.(重点)
学习重点:进一步掌握用一元一次方程解决实际问题的基本过程.
学习难点:学会利用线段图分析问题,找出等量关系,准确列出方程.
知识链接
1.行程问题
(1)慢车每小时行驶48千米,x小时可行驶
千米,快车每小时行驶72千米,如果快车先开小时,那么在慢车开出x小时后快车行驶
千米.
(2)路程、时间、平均速度之间有怎样的关系?
路程=___________
×
_____________;
时间=___________
÷
_____________
;
平均速度=___________
÷
_____________
。
2.工程问题
(1)一项工作甲独做5天完成,乙独做10天完成,那么甲每天的工作效率是
,乙每天的工作效率是
,两人合作3天完成的工作量是
,此时剩余的工作量是
.
(2)一项工作甲独做a天完成,乙独做b天完成,那么甲每天的工作效率是
,乙每天的工作效率是
,两人合作3天完成的工作量是
,此时剩余的工作量是
.
(3)工作量、工作时间、工作效率之间有怎样的关系?
工作量
=___________
×
_____________
;
工作时间=___________
÷
_____________
;
工作效率=___________
÷
_____________
.
新知预习
自主探究
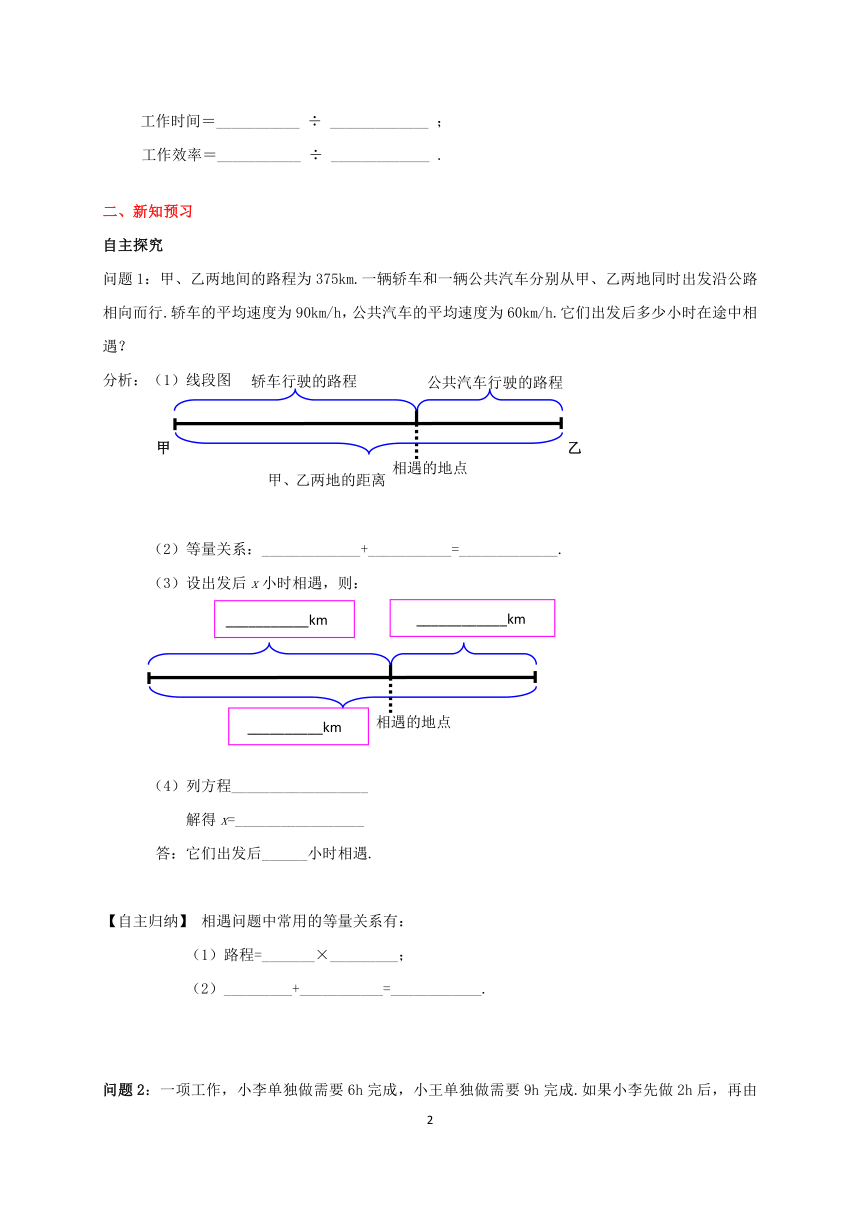
问题1:甲、乙两地间的路程为375km.一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行.轿车的平均速度为90km/h,公共汽车的平均速度为60km/h.它们出发后多少小时在途中相遇?
分析:(1)线段图
甲
乙
(2)等量关系:_____________+___________=_____________.
(3)设出发后x小时相遇,则:
(4)列方程__________________
解得x=_________________
答:它们出发后______小时相遇.
【自主归纳】
相遇问题中常用的等量关系有:
(1)路程=_______×_________;
(2)_________+___________=____________.
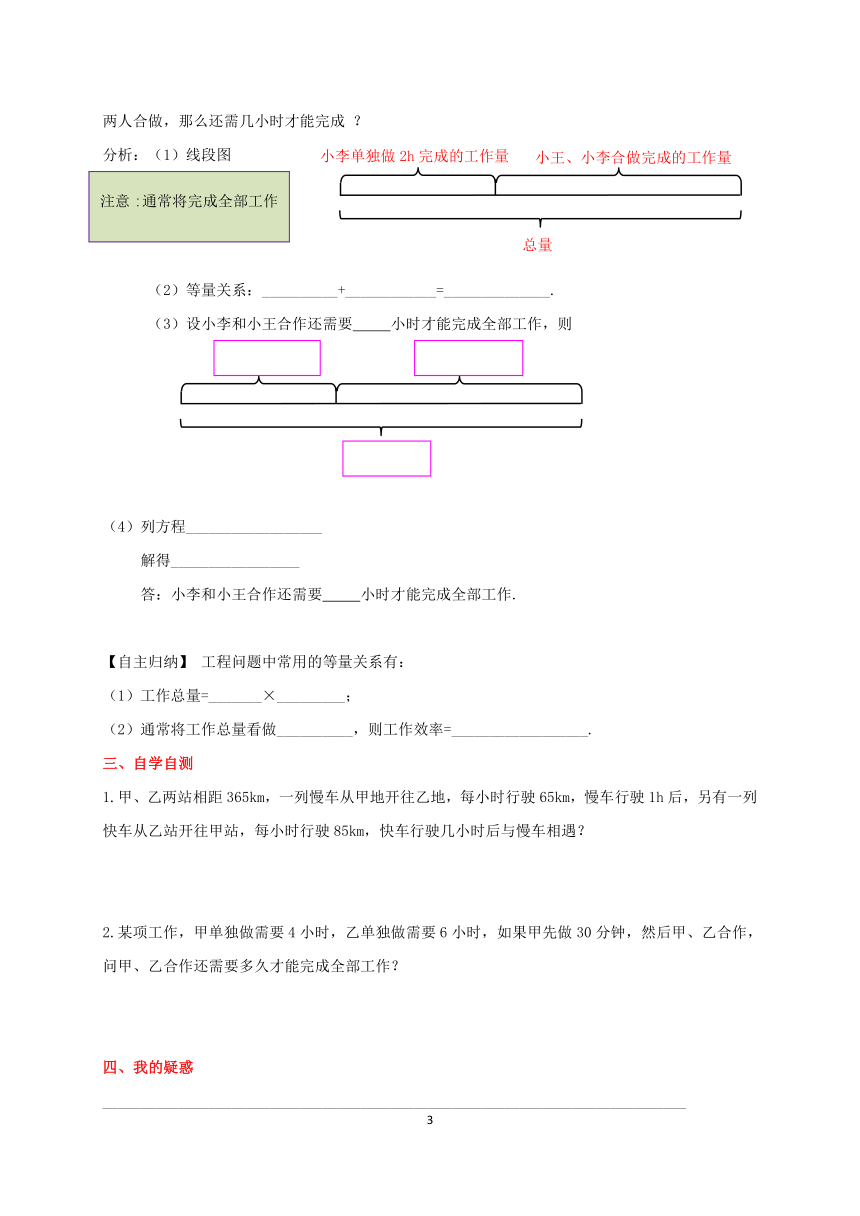
问题2:一项工作,小李单独做需要6h完成,小王单独做需要9h完成.如果小李先做2h后,再由两人合做,那么还需几小时才能完成
?
分析:(1)线段图
(2)等量关系:__________+____________=______________.
(3)设小李和小王合作还需要
小时才能完成全部工作,则
(4)列方程__________________
解得_________________
答:小李和小王合作还需要
小时才能完成全部工作.
【自主归纳】
工程问题中常用的等量关系有:
(1)工作总量=_______×_________;
(2)通常将工作总量看做__________,则工作效率=__________________.
自学自测
甲、乙两站相距365km,一列慢车从甲地开往乙地,每小时行驶65km,慢车行驶1h后,另有一列快车从乙站开往甲站,每小时行驶85km,快车行驶几小时后与慢车相遇?
2.某项工作,甲单独做需要4小时,乙单独做需要6小时,如果甲先做30分钟,然后甲、乙合作,问甲、乙合作还需要多久才能完成全部工作?
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:相遇问题
例1:小明家离学校2.9千米,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明?
【归纳总结】找出问题中的等量关系是列方程解应用题的关键,对于行程问题,通常借助“线段图”来分析问题中的数量关系.这样可以比较直观地反映出方程中的等量关系.此外,注意单位要统一.
例2:甲、乙两人在一条长400米的环形跑道上跑步,甲的速度为360米/分,乙的速度是240米/分.两人同时同地反向跑,问几秒后两人第一次相遇?
【归纳总结】环形问题中的等量关系:两个人同地背向而行:相遇问题(首次相遇),甲的行程+乙的行程=一圈周长.
【针对训练】
1.甲、乙两人骑自行车同时从相距65千米的两地相向而行,2小时相遇,若甲比乙每小时多骑2.5千米,求乙的速度.
2.甲、乙两人在环形跑道上练习跑步,已知跑道一圈长400m,甲每秒钟跑6m,乙每秒钟跑8m,如果甲、乙两人在跑道上相距8m,同时反向出发,那么经过几秒两人首次相遇?
探究点2:工程问题
例3:一个道路工程,甲队单独施工9天完成,乙队单独做24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,问乙队还需几天才能完成?
【归纳总结】在工程问题中,如果工作总量没有明确给出,将工作总量设为1是常用的解决办法.工程问题中常用的相等关系有:(1)按工作时间,各时间段的工作量之和=完成的工作量.
(2)按工作者,若一项工作有甲、乙两人参与,则甲的工作量+乙的工作量=完成的工作量.
【针对训练】
整理一批图书,由一个人做要40小时完成。现在计划由一部分人先做4小时,再增加两人和他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应安排多少人工作?
二、课堂小结
内容
相遇问题
路程=_______×________;
__________+__________=总路程.
工程问题
工作总量=_______×________;
按工作时间:__________=______________;
按工作者:________+________=___________.
某公路的干线上有相距108公里的A.B两个车站,某日16点整,甲、乙两车分别从A.B两站同时出发,相向而行,已知甲车的速度为45公里/时,乙车的速度为36公里/时,则两车相遇的时间是(
)
A.16时20分
B.17时20分
C.17时40分
D.16时40分
2.加工1
500个零件,甲单独做需要12小时,乙单独做需要15小时,若两人合做x小时可以完工,依题意可列方程为(
)
A.
B.
C.
D.
一项工程,甲队单独完成需要20天,乙队单独完成需要30天,如果先由甲队单独做5天,则剩下部分由甲、乙两队合作完成还需要的天数是(
)
A.9
B.10
C.12
D.15
4.A.B两地相距450千米,甲、乙两车分别从A.B两地同时出发,相向而行.已知甲车的速度为120千米/时,乙车的速度为80千米/时,t小时后两车相遇,则t=_______.
5.一项工程由甲单独做需12天完成,由乙单独做需8天完成,若两人合做3天后,剩下的部分由乙单独完成,乙还需做____天.
6.运动场的跑道一圈长400米,甲练习骑自行车,平均每分钟骑350米,乙练习跑步,平均每分钟跑250米.两人从同一处同时反向出发,经过多长时间首次相遇?
7.甲车由A城到B城需4小时,乙车由B城到A城需6小时,若两车同时出发,相向而行,多少小时在中途相遇?
8.一项工作,由1人做要40小时完成,现计划由2人先做4小时,剩下的工作要8小时完成,问还需增加几人?(假定每个人的工作效率都相同)
9.一件工作由一个人做要500小时完成,现在计划由一部分人先做5小时,再增加8人和他们一起做10小时,完成了这项工作,问:先安排多少人工作?
10.电气机车和磁悬浮列车从相距298千米的两地同时出发相对而行,磁悬浮列车的速度比电气机车速度的5倍还快20千米/时,半小时后两车相遇.两车的速度各是多少?
当堂检测参考答案:
B
2.B
3.A
4.
2.25
5.
3
6.解:设x分钟后首次相遇,由题意得
350x+250x=400
解得x=
答:二人经过分钟后首次相遇.
7.解:设x小时后两车在途中相遇,由题意得
解得
x=2.4.
答:经过2.4小时后两车在途中相遇.
8.解:设还需增加x人,由题意得
.
解得
x=2.
答:还需增加2人.
9.解:设先安排x人工作,由题意得
解得
x=28.
答:先安排28人工作.
10.解:设电气机车的速度为xkm/h,则磁悬浮列车的速度为(5x+20)km/h,由题意得
.
解得
x=96,
故
5x+20=500.
答:电气机车的速度为96km/h,磁悬浮列车的速度为500km/h.
1
一元一次方程的应用
第2课时
列一元一次方程解决相遇问题、工程问题
学习目标:
1.掌握相遇问题、工程问题中的基本等量关系;
2.学会利用线段图分析相遇问题及工程问题,分清有关数量关系,正确找出作为列方程依据的主要等量关系;(难点)
3.进一步掌握用一元一次方程解决实际问题的基本过程.(重点)
学习重点:进一步掌握用一元一次方程解决实际问题的基本过程.
学习难点:学会利用线段图分析问题,找出等量关系,准确列出方程.
知识链接
1.行程问题
(1)慢车每小时行驶48千米,x小时可行驶
千米,快车每小时行驶72千米,如果快车先开小时,那么在慢车开出x小时后快车行驶
千米.
(2)路程、时间、平均速度之间有怎样的关系?
路程=___________
×
_____________;
时间=___________
÷
_____________
;
平均速度=___________
÷
_____________
。
2.工程问题
(1)一项工作甲独做5天完成,乙独做10天完成,那么甲每天的工作效率是
,乙每天的工作效率是
,两人合作3天完成的工作量是
,此时剩余的工作量是
.
(2)一项工作甲独做a天完成,乙独做b天完成,那么甲每天的工作效率是
,乙每天的工作效率是
,两人合作3天完成的工作量是
,此时剩余的工作量是
.
(3)工作量、工作时间、工作效率之间有怎样的关系?
工作量
=___________
×
_____________
;
工作时间=___________
÷
_____________
;
工作效率=___________
÷
_____________
.
新知预习
自主探究
问题1:甲、乙两地间的路程为375km.一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行.轿车的平均速度为90km/h,公共汽车的平均速度为60km/h.它们出发后多少小时在途中相遇?
分析:(1)线段图
甲
乙
(2)等量关系:_____________+___________=_____________.
(3)设出发后x小时相遇,则:
(4)列方程__________________
解得x=_________________
答:它们出发后______小时相遇.
【自主归纳】
相遇问题中常用的等量关系有:
(1)路程=_______×_________;
(2)_________+___________=____________.
问题2:一项工作,小李单独做需要6h完成,小王单独做需要9h完成.如果小李先做2h后,再由两人合做,那么还需几小时才能完成
?
分析:(1)线段图
(2)等量关系:__________+____________=______________.
(3)设小李和小王合作还需要
小时才能完成全部工作,则
(4)列方程__________________
解得_________________
答:小李和小王合作还需要
小时才能完成全部工作.
【自主归纳】
工程问题中常用的等量关系有:
(1)工作总量=_______×_________;
(2)通常将工作总量看做__________,则工作效率=__________________.
自学自测
甲、乙两站相距365km,一列慢车从甲地开往乙地,每小时行驶65km,慢车行驶1h后,另有一列快车从乙站开往甲站,每小时行驶85km,快车行驶几小时后与慢车相遇?
2.某项工作,甲单独做需要4小时,乙单独做需要6小时,如果甲先做30分钟,然后甲、乙合作,问甲、乙合作还需要多久才能完成全部工作?
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:相遇问题
例1:小明家离学校2.9千米,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明?
【归纳总结】找出问题中的等量关系是列方程解应用题的关键,对于行程问题,通常借助“线段图”来分析问题中的数量关系.这样可以比较直观地反映出方程中的等量关系.此外,注意单位要统一.
例2:甲、乙两人在一条长400米的环形跑道上跑步,甲的速度为360米/分,乙的速度是240米/分.两人同时同地反向跑,问几秒后两人第一次相遇?
【归纳总结】环形问题中的等量关系:两个人同地背向而行:相遇问题(首次相遇),甲的行程+乙的行程=一圈周长.
【针对训练】
1.甲、乙两人骑自行车同时从相距65千米的两地相向而行,2小时相遇,若甲比乙每小时多骑2.5千米,求乙的速度.
2.甲、乙两人在环形跑道上练习跑步,已知跑道一圈长400m,甲每秒钟跑6m,乙每秒钟跑8m,如果甲、乙两人在跑道上相距8m,同时反向出发,那么经过几秒两人首次相遇?
探究点2:工程问题
例3:一个道路工程,甲队单独施工9天完成,乙队单独做24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,问乙队还需几天才能完成?
【归纳总结】在工程问题中,如果工作总量没有明确给出,将工作总量设为1是常用的解决办法.工程问题中常用的相等关系有:(1)按工作时间,各时间段的工作量之和=完成的工作量.
(2)按工作者,若一项工作有甲、乙两人参与,则甲的工作量+乙的工作量=完成的工作量.
【针对训练】
整理一批图书,由一个人做要40小时完成。现在计划由一部分人先做4小时,再增加两人和他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应安排多少人工作?
二、课堂小结
内容
相遇问题
路程=_______×________;
__________+__________=总路程.
工程问题
工作总量=_______×________;
按工作时间:__________=______________;
按工作者:________+________=___________.
某公路的干线上有相距108公里的A.B两个车站,某日16点整,甲、乙两车分别从A.B两站同时出发,相向而行,已知甲车的速度为45公里/时,乙车的速度为36公里/时,则两车相遇的时间是(
)
A.16时20分
B.17时20分
C.17时40分
D.16时40分
2.加工1
500个零件,甲单独做需要12小时,乙单独做需要15小时,若两人合做x小时可以完工,依题意可列方程为(
)
A.
B.
C.
D.
一项工程,甲队单独完成需要20天,乙队单独完成需要30天,如果先由甲队单独做5天,则剩下部分由甲、乙两队合作完成还需要的天数是(
)
A.9
B.10
C.12
D.15
4.A.B两地相距450千米,甲、乙两车分别从A.B两地同时出发,相向而行.已知甲车的速度为120千米/时,乙车的速度为80千米/时,t小时后两车相遇,则t=_______.
5.一项工程由甲单独做需12天完成,由乙单独做需8天完成,若两人合做3天后,剩下的部分由乙单独完成,乙还需做____天.
6.运动场的跑道一圈长400米,甲练习骑自行车,平均每分钟骑350米,乙练习跑步,平均每分钟跑250米.两人从同一处同时反向出发,经过多长时间首次相遇?
7.甲车由A城到B城需4小时,乙车由B城到A城需6小时,若两车同时出发,相向而行,多少小时在中途相遇?
8.一项工作,由1人做要40小时完成,现计划由2人先做4小时,剩下的工作要8小时完成,问还需增加几人?(假定每个人的工作效率都相同)
9.一件工作由一个人做要500小时完成,现在计划由一部分人先做5小时,再增加8人和他们一起做10小时,完成了这项工作,问:先安排多少人工作?
10.电气机车和磁悬浮列车从相距298千米的两地同时出发相对而行,磁悬浮列车的速度比电气机车速度的5倍还快20千米/时,半小时后两车相遇.两车的速度各是多少?
当堂检测参考答案:
B
2.B
3.A
4.
2.25
5.
3
6.解:设x分钟后首次相遇,由题意得
350x+250x=400
解得x=
答:二人经过分钟后首次相遇.
7.解:设x小时后两车在途中相遇,由题意得
解得
x=2.4.
答:经过2.4小时后两车在途中相遇.
8.解:设还需增加x人,由题意得
.
解得
x=2.
答:还需增加2人.
9.解:设先安排x人工作,由题意得
解得
x=28.
答:先安排28人工作.
10.解:设电气机车的速度为xkm/h,则磁悬浮列车的速度为(5x+20)km/h,由题意得
.
解得
x=96,
故
5x+20=500.
答:电气机车的速度为96km/h,磁悬浮列车的速度为500km/h.
1
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
