人教版九年级上册数学中考真题分类(选择题)专练:24.1圆有关系的性质综合(word版,含解析)
文档属性
| 名称 | 人教版九年级上册数学中考真题分类(选择题)专练:24.1圆有关系的性质综合(word版,含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 252.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 00:00:00 | ||
图片预览


文档简介
人教版九年级上册数学中考真题分类(选择题)专练:
24.1圆有关系的性质综合
1.(2020?阜新)如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A.57°
B.52°
C.38°
D.26°
2.(2020?眉山)如图,四边形ABCD的外接圆为⊙O,BC=CD,∠DAC=35°,∠ACD=45°,则∠ADB的度数为( )
A.55°
B.60°
C.65°
D.70°
3.(2020?长春)如图,AB是⊙O的直径,点C、D在⊙O上,∠BDC=20°,则∠AOC的大小为( )
A.40°
B.140°
C.160°
D.170°
4.(2020?镇江)如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
A.10°
B.14°
C.16°
D.26°
5.(2020?吉林)如图,四边形ABCD内接于⊙O,若∠B=108°,则∠D的大小为( )
A.54°
B.62°
C.72°
D.82°
6.(2020?海南)如图,已知AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
A.54°
B.56°
C.64°
D.66°
7.(2020?十堰)如图,点A,B,C,D在⊙O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
A.2
B.4
C.
D.2
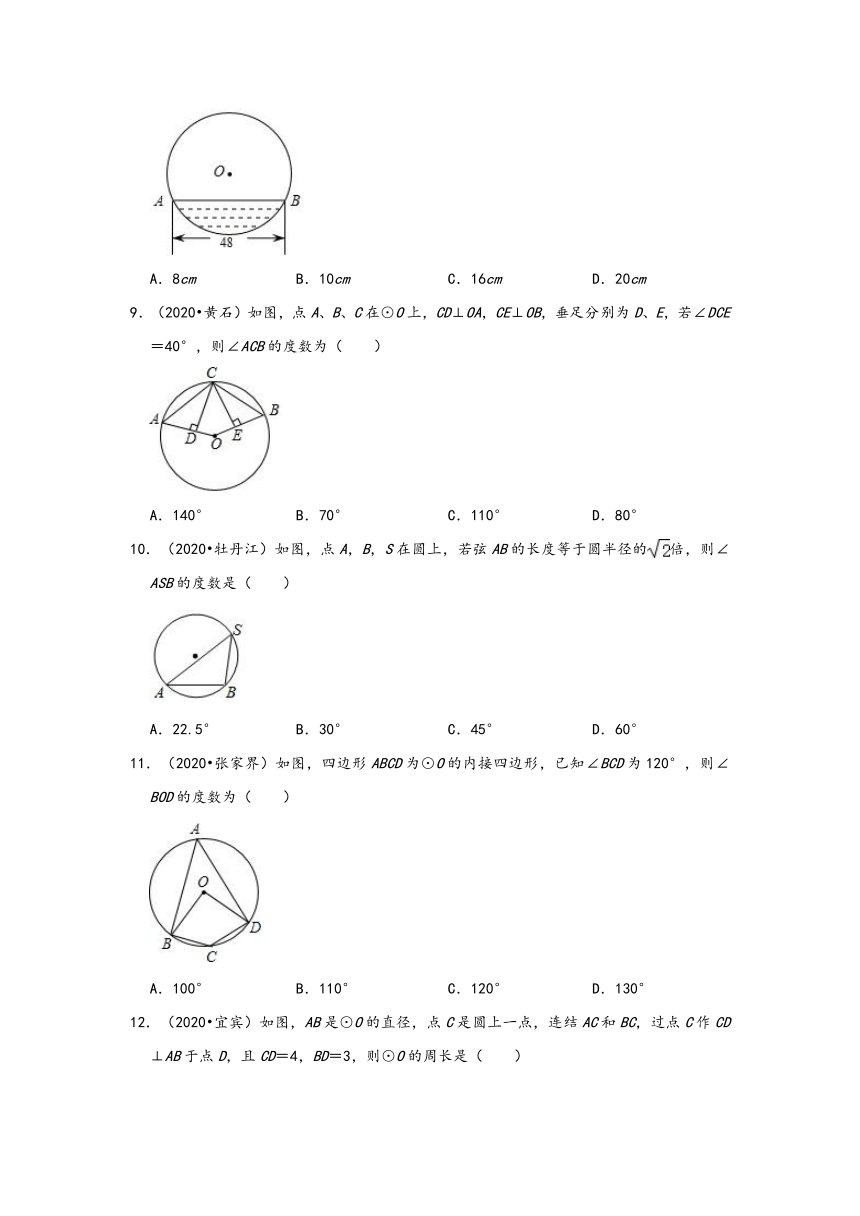
8.(2020?广州)往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
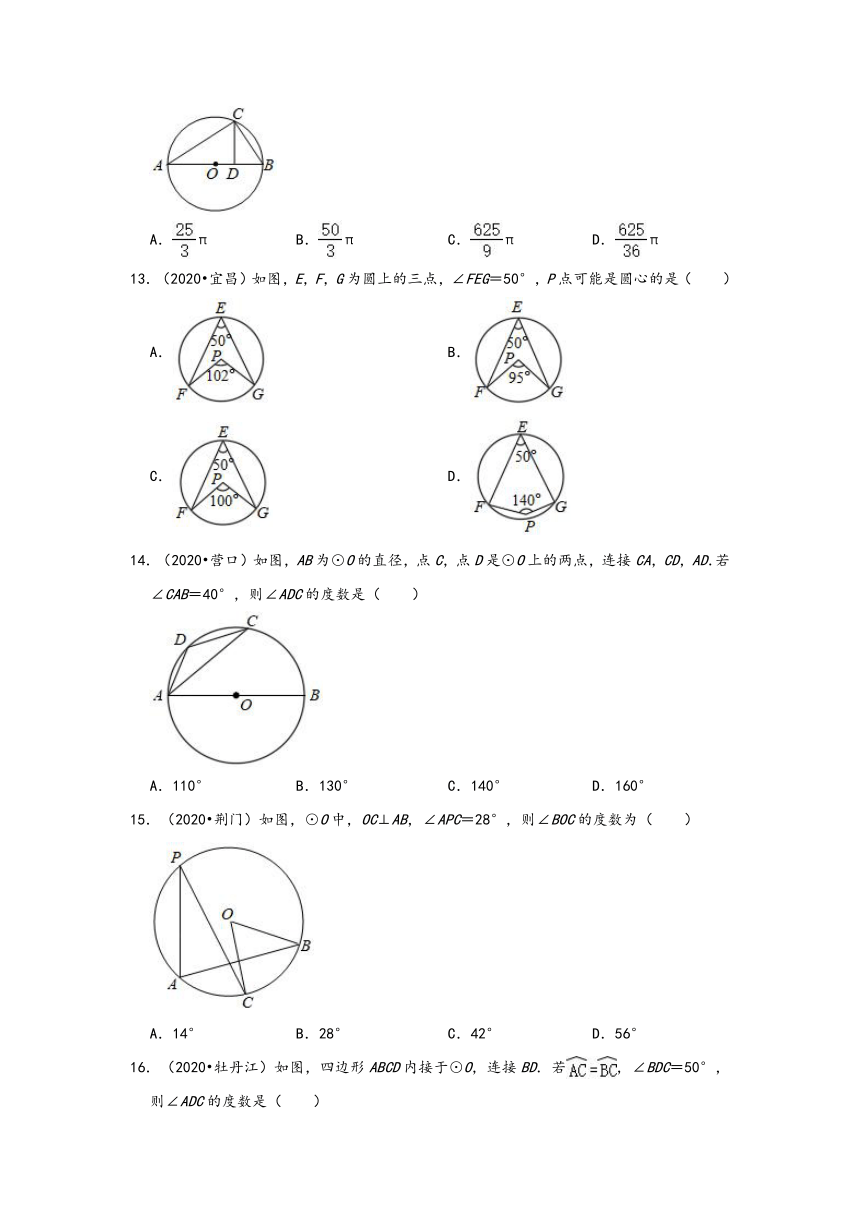
9.(2020?黄石)如图,点A、B、C在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D、E,若∠DCE=40°,则∠ACB的度数为( )
A.140°
B.70°
C.110°
D.80°
10.(2020?牡丹江)如图,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是( )
A.22.5°
B.30°
C.45°
D.60°
11.(2020?张家界)如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100°
B.110°
C.120°
D.130°
12.(2020?宜宾)如图,AB是⊙O的直径,点C是圆上一点,连结AC和BC,过点C作CD⊥AB于点D,且CD=4,BD=3,则⊙O的周长是( )
A.π
B.π
C.π
D.π
13.(2020?宜昌)如图,E,F,G为圆上的三点,∠FEG=50°,P点可能是圆心的是( )
A.
B.
C.
D.
14.(2020?营口)如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )
A.110°
B.130°
C.140°
D.160°
15.(2020?荆门)如图,⊙O中,OC⊥AB,∠APC=28°,则∠BOC的度数为( )
A.14°
B.28°
C.42°
D.56°
16.(2020?牡丹江)如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125°
B.130°
C.135°
D.140°
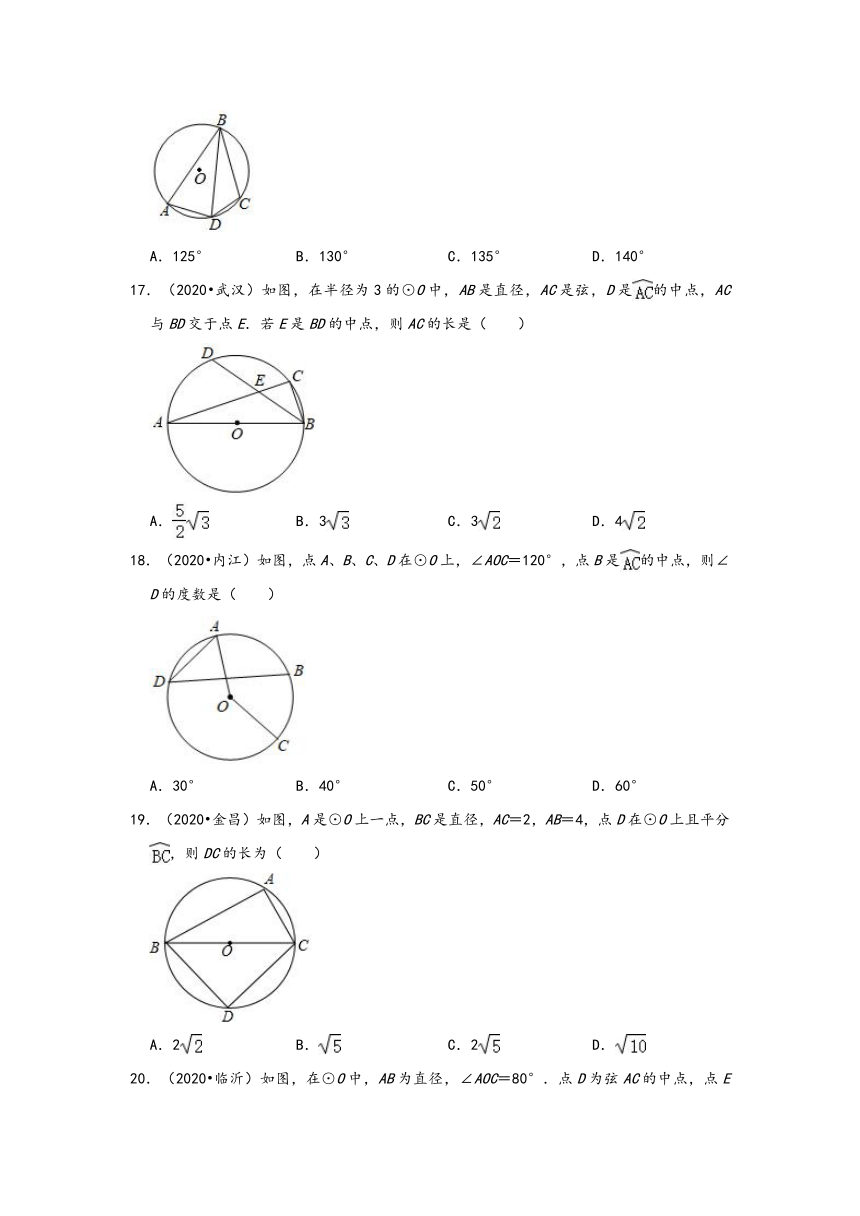
17.(2020?武汉)如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
18.(2020?内江)如图,点A、B、C、D在⊙O上,∠AOC=120°,点B是的中点,则∠D的度数是( )
A.30°
B.40°
C.50°
D.60°
19.(2020?金昌)如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分,则DC的长为( )
A.2
B.
C.2
D.
20.(2020?临沂)如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
参考答案
1.解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=38°,
∴∠BAC=90°﹣∠ABC=52°,
∴∠BDC=∠BAC=52°.
故选:B.
2.解:∵BC=CD,
∴=,
∵∠ABD和∠ACD所对的弧都是,
∴∠BAC=∠DAC=35°,
∵∠ABD=∠ACD=45°,
∴∠ADB=180°﹣∠BAD﹣∠ABD=180°﹣70°﹣45°=65°.
故选:C.
3.解:∵∠BOC=2∠BDC=2×20°=40°,
∴∠AOC=180°﹣40°=140°.
故选:B.
4.解:连接BD,如图,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠BDC=∠ADC﹣∠ADB=106°﹣90°=16°,
∴∠CAB=∠BDC=16°.
故选:C.
5.解:∵四边形ABCD内接于⊙O,∠B=108°,
∴∠D=180°﹣∠B=180°﹣108°=72°,
故选:C.
6.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠DAB=∠BCD=36°,
∴∠ABD=∠ADB﹣∠DAB,
即∠ABD=90°﹣∠DAB=90°﹣36°=54°.
故选:A.
7.解:连接OC,如图,
∵∠ADC=30°,
∴∠AOC=60°,
∵OA⊥BC,
∴CE=BE,
在Rt△COE中,OE=OC,CE=OE,
∵OE=OA﹣AE=OC﹣1,
∴OC﹣1=OC,
∴OC=2,
∴OE=1,
∴CE=,
∴BC=2CE=2.
故选:D.
8.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
9.解:如图,在优弧AB上取一点P,连接AP,BP,
∵CD⊥OA,CE⊥OB,
∴∠ODC=∠OEC=90°,
∵∠DCE=40°,
∴∠AOB=360°﹣90°﹣90°﹣40°=140°,
∴∠P=∠AOB=70°,
∵A、C、B、P四点共圆,
∴∠P+∠ACB=180°,
∴∠ACB=180°﹣70°=110°,
故选:C.
10.解:设圆心为O,连接OA、OB,如图,
∵弦AB的长度等于圆半径的倍,
即AB=OA,
∴OA2+OB2=AB2,
∴∠AOB=90°,
∴∠ASB=∠AOB=45°.
故选:C.
11.解:∵四边形ABCD是⊙O的内接四边形,
∴∠A=180°﹣∠BCD=60°,
由圆周角定理得,∠BOD=2∠A=120°,
故选:C.
12.解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD⊥AB,
∴Rt△ABC∽Rt△CBD,
∴,
∵CD=4,BD=3,
∴BC===5
∴,
∴AB=,
∴⊙O的周长是π,
故选:A.
13.解:∵∠FEG=50°,
若P点圆心,
∴∠FPG=2∠FEG=100°.
故选:C.
14.解:如图,连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠CAB=90°﹣40°=50°,
∵∠B+∠ADC=180°,
∴∠ADC=180°﹣50°=130°.
故选:B.
15.解:∵在⊙O中,OC⊥AB,
∴=,
∵∠APC=28°,
∴∠BOC=2∠APC=56°,
故选:D.
16.解:连接OA,OB,OC,
∵∠BDC=50°,
∴∠BOC=2∠BDC=100°,
∵,
∴∠BOC=∠AOC=100°,
∴∠ABC=∠AOC=50°,
∴∠ADC=180°﹣∠ABC=130°.
故选:B.
17.解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
18.解:连接OB,如图,
∵点B是的中点,
∴∠AOB=∠AOC=×120°=60°,
∴∠D=∠AOB=30°.
故选:A.
19.解:∵BC是⊙O的直径,
∴∠BAC=∠D=90°,
∵AC=2,AB=4,
∴BC===2,
∵点D在⊙O上,且平分,
∴DC=BD.
Rt△BDC中,DC2+BD2=BC2,
∴2DC2=20,
∴DC=,
故选:D.
20.解:连接OD、OE,
∵OC=OA,
∴△OAC是等腰三角形,
∵点D为弦AC的中点,
∴∠DOC=40°,∠BOC=100°,
设∠BOE=x,则∠COE=100°﹣x,∠DOE=100°﹣x+40°,
∵OC=OE,∠COE=100°﹣x,
∴∠OEC=∠OCE=40°+x,
∵OD<OE,∠DOE=100°﹣x+40°=140°﹣x,
∴∠OED<20°+x,
∴∠CED=∠OEC﹣∠OED>(40°+x)﹣(20°+x)=20°,
∵∠CED<∠ABC=40°,
∴20°<∠CED<40°
故选:C.
24.1圆有关系的性质综合
1.(2020?阜新)如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A.57°
B.52°
C.38°
D.26°
2.(2020?眉山)如图,四边形ABCD的外接圆为⊙O,BC=CD,∠DAC=35°,∠ACD=45°,则∠ADB的度数为( )
A.55°
B.60°
C.65°
D.70°
3.(2020?长春)如图,AB是⊙O的直径,点C、D在⊙O上,∠BDC=20°,则∠AOC的大小为( )
A.40°
B.140°
C.160°
D.170°
4.(2020?镇江)如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
A.10°
B.14°
C.16°
D.26°
5.(2020?吉林)如图,四边形ABCD内接于⊙O,若∠B=108°,则∠D的大小为( )
A.54°
B.62°
C.72°
D.82°
6.(2020?海南)如图,已知AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
A.54°
B.56°
C.64°
D.66°
7.(2020?十堰)如图,点A,B,C,D在⊙O上,OA⊥BC,垂足为E.若∠ADC=30°,AE=1,则BC=( )
A.2
B.4
C.
D.2
8.(2020?广州)往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
9.(2020?黄石)如图,点A、B、C在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D、E,若∠DCE=40°,则∠ACB的度数为( )
A.140°
B.70°
C.110°
D.80°
10.(2020?牡丹江)如图,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是( )
A.22.5°
B.30°
C.45°
D.60°
11.(2020?张家界)如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100°
B.110°
C.120°
D.130°
12.(2020?宜宾)如图,AB是⊙O的直径,点C是圆上一点,连结AC和BC,过点C作CD⊥AB于点D,且CD=4,BD=3,则⊙O的周长是( )
A.π
B.π
C.π
D.π
13.(2020?宜昌)如图,E,F,G为圆上的三点,∠FEG=50°,P点可能是圆心的是( )
A.
B.
C.
D.
14.(2020?营口)如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )
A.110°
B.130°
C.140°
D.160°
15.(2020?荆门)如图,⊙O中,OC⊥AB,∠APC=28°,则∠BOC的度数为( )
A.14°
B.28°
C.42°
D.56°
16.(2020?牡丹江)如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125°
B.130°
C.135°
D.140°
17.(2020?武汉)如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
18.(2020?内江)如图,点A、B、C、D在⊙O上,∠AOC=120°,点B是的中点,则∠D的度数是( )
A.30°
B.40°
C.50°
D.60°
19.(2020?金昌)如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分,则DC的长为( )
A.2
B.
C.2
D.
20.(2020?临沂)如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
参考答案
1.解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=38°,
∴∠BAC=90°﹣∠ABC=52°,
∴∠BDC=∠BAC=52°.
故选:B.
2.解:∵BC=CD,
∴=,
∵∠ABD和∠ACD所对的弧都是,
∴∠BAC=∠DAC=35°,
∵∠ABD=∠ACD=45°,
∴∠ADB=180°﹣∠BAD﹣∠ABD=180°﹣70°﹣45°=65°.
故选:C.
3.解:∵∠BOC=2∠BDC=2×20°=40°,
∴∠AOC=180°﹣40°=140°.
故选:B.
4.解:连接BD,如图,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠BDC=∠ADC﹣∠ADB=106°﹣90°=16°,
∴∠CAB=∠BDC=16°.
故选:C.
5.解:∵四边形ABCD内接于⊙O,∠B=108°,
∴∠D=180°﹣∠B=180°﹣108°=72°,
故选:C.
6.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠DAB=∠BCD=36°,
∴∠ABD=∠ADB﹣∠DAB,
即∠ABD=90°﹣∠DAB=90°﹣36°=54°.
故选:A.
7.解:连接OC,如图,
∵∠ADC=30°,
∴∠AOC=60°,
∵OA⊥BC,
∴CE=BE,
在Rt△COE中,OE=OC,CE=OE,
∵OE=OA﹣AE=OC﹣1,
∴OC﹣1=OC,
∴OC=2,
∴OE=1,
∴CE=,
∴BC=2CE=2.
故选:D.
8.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
9.解:如图,在优弧AB上取一点P,连接AP,BP,
∵CD⊥OA,CE⊥OB,
∴∠ODC=∠OEC=90°,
∵∠DCE=40°,
∴∠AOB=360°﹣90°﹣90°﹣40°=140°,
∴∠P=∠AOB=70°,
∵A、C、B、P四点共圆,
∴∠P+∠ACB=180°,
∴∠ACB=180°﹣70°=110°,
故选:C.
10.解:设圆心为O,连接OA、OB,如图,
∵弦AB的长度等于圆半径的倍,
即AB=OA,
∴OA2+OB2=AB2,
∴∠AOB=90°,
∴∠ASB=∠AOB=45°.
故选:C.
11.解:∵四边形ABCD是⊙O的内接四边形,
∴∠A=180°﹣∠BCD=60°,
由圆周角定理得,∠BOD=2∠A=120°,
故选:C.
12.解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD⊥AB,
∴Rt△ABC∽Rt△CBD,
∴,
∵CD=4,BD=3,
∴BC===5
∴,
∴AB=,
∴⊙O的周长是π,
故选:A.
13.解:∵∠FEG=50°,
若P点圆心,
∴∠FPG=2∠FEG=100°.
故选:C.
14.解:如图,连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠CAB=90°﹣40°=50°,
∵∠B+∠ADC=180°,
∴∠ADC=180°﹣50°=130°.
故选:B.
15.解:∵在⊙O中,OC⊥AB,
∴=,
∵∠APC=28°,
∴∠BOC=2∠APC=56°,
故选:D.
16.解:连接OA,OB,OC,
∵∠BDC=50°,
∴∠BOC=2∠BDC=100°,
∵,
∴∠BOC=∠AOC=100°,
∴∠ABC=∠AOC=50°,
∴∠ADC=180°﹣∠ABC=130°.
故选:B.
17.解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
18.解:连接OB,如图,
∵点B是的中点,
∴∠AOB=∠AOC=×120°=60°,
∴∠D=∠AOB=30°.
故选:A.
19.解:∵BC是⊙O的直径,
∴∠BAC=∠D=90°,
∵AC=2,AB=4,
∴BC===2,
∵点D在⊙O上,且平分,
∴DC=BD.
Rt△BDC中,DC2+BD2=BC2,
∴2DC2=20,
∴DC=,
故选:D.
20.解:连接OD、OE,
∵OC=OA,
∴△OAC是等腰三角形,
∵点D为弦AC的中点,
∴∠DOC=40°,∠BOC=100°,
设∠BOE=x,则∠COE=100°﹣x,∠DOE=100°﹣x+40°,
∵OC=OE,∠COE=100°﹣x,
∴∠OEC=∠OCE=40°+x,
∵OD<OE,∠DOE=100°﹣x+40°=140°﹣x,
∴∠OED<20°+x,
∴∠CED=∠OEC﹣∠OED>(40°+x)﹣(20°+x)=20°,
∵∠CED<∠ABC=40°,
∴20°<∠CED<40°
故选:C.
同课章节目录
