13.1.2 线段的垂直平分线的性质同步练习题(含答案)
文档属性
| 名称 | 13.1.2 线段的垂直平分线的性质同步练习题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-20 20:19:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十三章 轴对称
13.1.2 线段的垂直平分线的性质
练习
一、单选题(共10小题)
1.(2020·张家口市期中)到三角形三个顶点的距离相等的点是三角形( )的交点.
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高
2.(2019·保定市期中)如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
A.8 B.9 C.10 D.11
3.(2020·龙岗区期中)如图,已知,以两点为圆心,大于的长为半径画圆,两弧相交于点,连接与相较于点,则的周长为( )
A.8 B.10 C.11 D.13
4.(2019·深圳市期中)如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )
A.65° B.60°
C.55° D.45°
5.(2020·邵阳市期末)如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
6.(2020·滁州市期末)如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
A.1cm B.2cm C.3cm D.4cm
7.(2019·聊城市期中)如图,DE垂直平分AB,交AC于点D,交AB于点E,连接BD,若AC=6cm,BC=4cm,则△BCD的周长为( )
A.6cm B.8cm C.10cm D.12cm
8.(2018·青岛市期中)在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在的( )
A.三边中垂线的交点 B.三边中线的交点
C.三条角平分线的交点 D.三边上高的交点
9.(2019·德州市期末)如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )
A.8 B.11 C.16 D.17
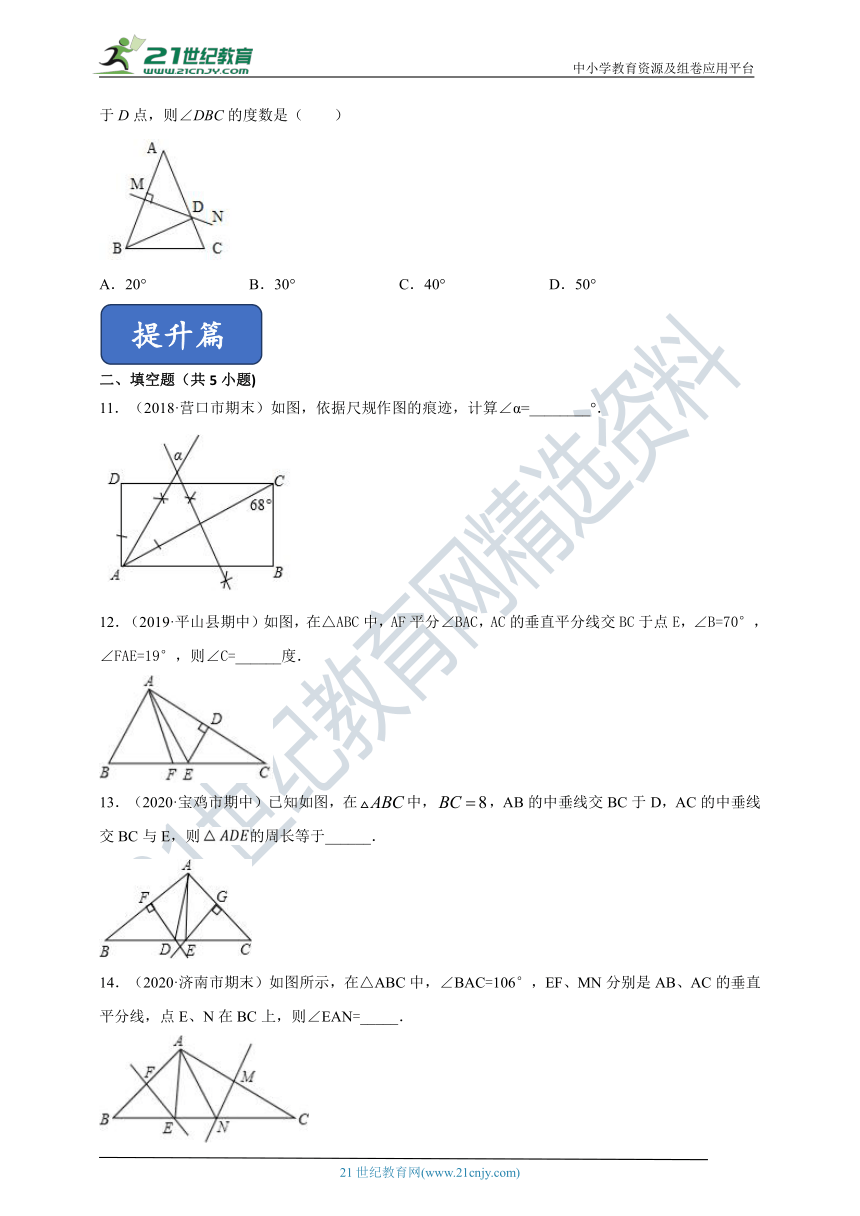
10.(2018·巴彦淖尔市中)如图,在△ABC 中,AB =AC ,∠A= 40°,AB 的垂直平分线MN 交 AC 于D点,则∠DBC的度数是( )
A.20° B.30° C.40° D.50°
二、填空题(共5小题)
11.(2018·营口市期末)如图,依据尺规作图的痕迹,计算∠α=________°.
12.(2019·平山县期中)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C=______度.
13.(2020·宝鸡市期中)已知如图,在中,,AB的中垂线交BC于D,AC的中垂线交BC与E,则的周长等于______.
14.(2020·济南市期末)如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=_____.
15.(2019·上饶市期中)如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是______.
三、解答题(共2小题)
16.(2019·淄博市期中)尺规作图:校园有两条路OA、OB,在交叉路口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置P.(不写画图过程,保留作图痕迹)
17.(2020·白银市期中)如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
答案
一、单选题(共10小题)
1.B.2.C3.A4.A.5.A.6.C.7.C.8.A.9.B10.B
二、填空题(共5小题)
11.【答案】56.【详解】如图,
∵四边形ABCD是矩形,∴AD∥BC,
∴∠DAC=∠ACB=68°.
∵由作法可知,AF是∠DAC的平分线,
∴∠EAF=∠DAC=34°.
∵由作法可知,EF是线段AC的垂直平分线,
∴∠AEF=90°,
∴∠AFE=90°-34°=56°,
∴∠α=56°.
故答案为:56.
12.【答案】24【详解】
∵DE是AC的垂直平分线,
∴EA=EC,
∠EAC=∠C,
∴∠FAC=∠FAE+∠EAC=19°+∠EAC,
∵AF平分∠BAC,
∴∠FAB=∠FAC.
在△ABC中,∠B+∠C+∠BAC=180°所以70°+∠C+2∠FAC=180°,
∴70°+∠EAC+2×(19°+∠EAC)=180° ,
∴∠C=∠EAC=24°,
故本题正确答案为24.
13.【答案】8【解析】
因为AB的中垂线交BC于D,AC的中垂线交BC与E,所以AD=DB,AE=CE.
△ADE的周长为AD+DE+AE=BD+DE+EC=BC=8.
故答案为8.
14.【答案】32°【详解】
解:在△ABC中,∠BAC=106°,
∴∠B+∠C=180°?∠BAC=180°?106°=74°,
∵EF、MN分别是AB、AC的中垂线,
∴∠B=∠BAE,∠C=∠CAN,
即∠B+∠C=∠BAE+∠CAN=74°,
∴∠EAN=∠BAC?(∠BAE+∠CAN)=106°?74°=32°.
故答案为32°.
15.【答案】40°【解析】
∵MP与NQ分别垂直平分AB和AC
∴∠B=∠BAP,∠QAC=∠C
∵∠BAC=110°,∴∠B+∠C=70°
又∵∠APQ=∠B+∠BAP
∠AQP=∠C+∠QAC
∴∠APQ+∠AQP=2∠B+2∠C=140°
在△APQ中
∠PAQ=180°-∠APQ-∠AQP
=180°-140°=40°
三、解答题(共2小题)
16.【答案】见解析.【详解】如图,点P为所作.
17.【答案】(1)65°(2)证明见解析【详解】
(1)∵AD平分∠BAC,∠BAC=50°,
∴∠EAD=∠BAC=25°,
∵DE⊥AB,
∴∠AED=90°,
∴∠ADE=90°-∠EAD=90°-25°=65°;
(2)∵DE⊥AB,
∴∠AED=90°=∠ACB,
又AD平分∠BAC,
∴∠DAE=∠DAC,
又∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,DE=DC
∴点A在线段CE的垂直平分线上,点D在线段CE的垂直平分线上,
∴直线AD是线段CE的垂直平分线.
_21?????????è?????(www.21cnjy.com)_
第十三章 轴对称
13.1.2 线段的垂直平分线的性质
练习
一、单选题(共10小题)
1.(2020·张家口市期中)到三角形三个顶点的距离相等的点是三角形( )的交点.
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高
2.(2019·保定市期中)如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
A.8 B.9 C.10 D.11
3.(2020·龙岗区期中)如图,已知,以两点为圆心,大于的长为半径画圆,两弧相交于点,连接与相较于点,则的周长为( )
A.8 B.10 C.11 D.13
4.(2019·深圳市期中)如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )
A.65° B.60°
C.55° D.45°
5.(2020·邵阳市期末)如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
6.(2020·滁州市期末)如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
A.1cm B.2cm C.3cm D.4cm
7.(2019·聊城市期中)如图,DE垂直平分AB,交AC于点D,交AB于点E,连接BD,若AC=6cm,BC=4cm,则△BCD的周长为( )
A.6cm B.8cm C.10cm D.12cm
8.(2018·青岛市期中)在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在的( )
A.三边中垂线的交点 B.三边中线的交点
C.三条角平分线的交点 D.三边上高的交点
9.(2019·德州市期末)如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )
A.8 B.11 C.16 D.17
10.(2018·巴彦淖尔市中)如图,在△ABC 中,AB =AC ,∠A= 40°,AB 的垂直平分线MN 交 AC 于D点,则∠DBC的度数是( )
A.20° B.30° C.40° D.50°
二、填空题(共5小题)
11.(2018·营口市期末)如图,依据尺规作图的痕迹,计算∠α=________°.
12.(2019·平山县期中)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C=______度.
13.(2020·宝鸡市期中)已知如图,在中,,AB的中垂线交BC于D,AC的中垂线交BC与E,则的周长等于______.
14.(2020·济南市期末)如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=_____.
15.(2019·上饶市期中)如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是______.
三、解答题(共2小题)
16.(2019·淄博市期中)尺规作图:校园有两条路OA、OB,在交叉路口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置P.(不写画图过程,保留作图痕迹)
17.(2020·白银市期中)如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
答案
一、单选题(共10小题)
1.B.2.C3.A4.A.5.A.6.C.7.C.8.A.9.B10.B
二、填空题(共5小题)
11.【答案】56.【详解】如图,
∵四边形ABCD是矩形,∴AD∥BC,
∴∠DAC=∠ACB=68°.
∵由作法可知,AF是∠DAC的平分线,
∴∠EAF=∠DAC=34°.
∵由作法可知,EF是线段AC的垂直平分线,
∴∠AEF=90°,
∴∠AFE=90°-34°=56°,
∴∠α=56°.
故答案为:56.
12.【答案】24【详解】
∵DE是AC的垂直平分线,
∴EA=EC,
∠EAC=∠C,
∴∠FAC=∠FAE+∠EAC=19°+∠EAC,
∵AF平分∠BAC,
∴∠FAB=∠FAC.
在△ABC中,∠B+∠C+∠BAC=180°所以70°+∠C+2∠FAC=180°,
∴70°+∠EAC+2×(19°+∠EAC)=180° ,
∴∠C=∠EAC=24°,
故本题正确答案为24.
13.【答案】8【解析】
因为AB的中垂线交BC于D,AC的中垂线交BC与E,所以AD=DB,AE=CE.
△ADE的周长为AD+DE+AE=BD+DE+EC=BC=8.
故答案为8.
14.【答案】32°【详解】
解:在△ABC中,∠BAC=106°,
∴∠B+∠C=180°?∠BAC=180°?106°=74°,
∵EF、MN分别是AB、AC的中垂线,
∴∠B=∠BAE,∠C=∠CAN,
即∠B+∠C=∠BAE+∠CAN=74°,
∴∠EAN=∠BAC?(∠BAE+∠CAN)=106°?74°=32°.
故答案为32°.
15.【答案】40°【解析】
∵MP与NQ分别垂直平分AB和AC
∴∠B=∠BAP,∠QAC=∠C
∵∠BAC=110°,∴∠B+∠C=70°
又∵∠APQ=∠B+∠BAP
∠AQP=∠C+∠QAC
∴∠APQ+∠AQP=2∠B+2∠C=140°
在△APQ中
∠PAQ=180°-∠APQ-∠AQP
=180°-140°=40°
三、解答题(共2小题)
16.【答案】见解析.【详解】如图,点P为所作.
17.【答案】(1)65°(2)证明见解析【详解】
(1)∵AD平分∠BAC,∠BAC=50°,
∴∠EAD=∠BAC=25°,
∵DE⊥AB,
∴∠AED=90°,
∴∠ADE=90°-∠EAD=90°-25°=65°;
(2)∵DE⊥AB,
∴∠AED=90°=∠ACB,
又AD平分∠BAC,
∴∠DAE=∠DAC,
又∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,DE=DC
∴点A在线段CE的垂直平分线上,点D在线段CE的垂直平分线上,
∴直线AD是线段CE的垂直平分线.
_21?????????è?????(www.21cnjy.com)_
