人教版高一物理必修一第二章 2.3位移和时间的关系 21张PPT
文档属性
| 名称 | 人教版高一物理必修一第二章 2.3位移和时间的关系 21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1004.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-21 08:39:32 | ||
图片预览







文档简介
(共25张PPT)
2.3、匀变速直线运动的
位移和时间的关系
一、匀速直线运动的位移和时间的关系
v/m.s
-1
t/s
0
5
2
2.在速度-时间图象中:
图像与坐标轴所围的面积在数值上等于位移大小。
1.用公式表述:X=vt
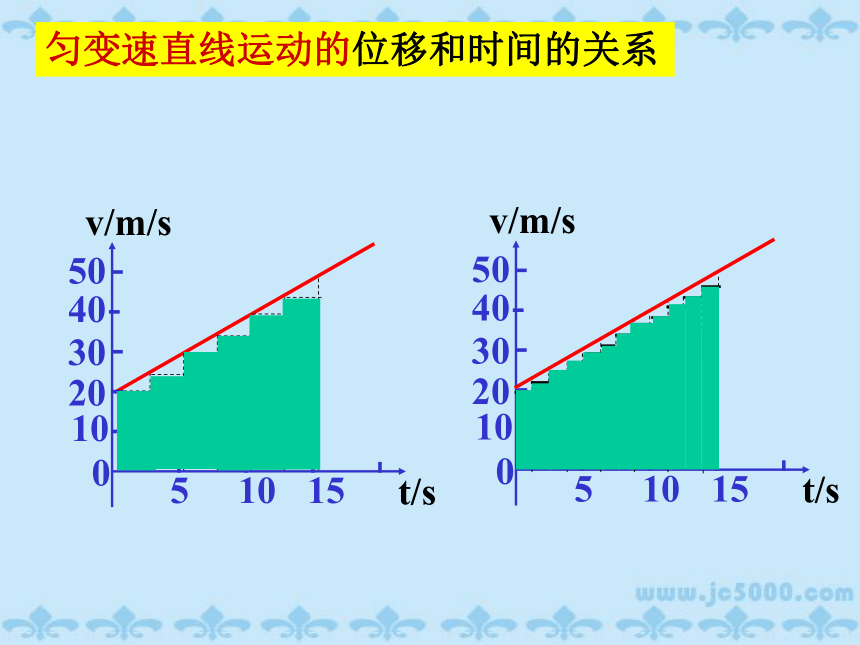
思考
匀变速直线运动的位移是否可用
图线与坐标轴所围的面积表示
匀变速直线运动的位移和时间的关系
v/m/s
0
20
40
5
10
15
30
t/s
50
10
v/m/s
0
20
40
5
10
15
30
t/s
50
10
v/m/s
0
20
40
5
10
15
30
t/s
50
10
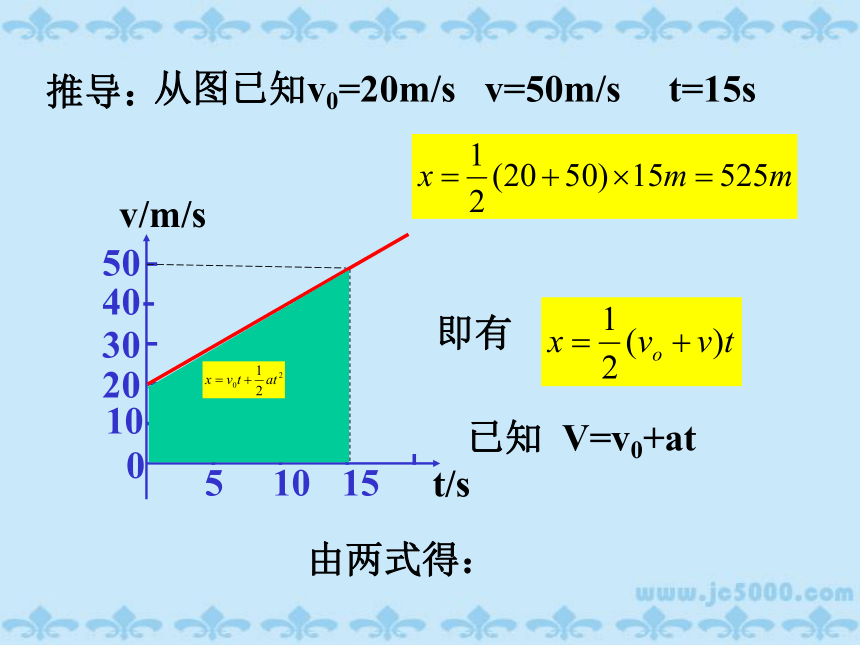
从图已知v0=20m/s
v=50m/s
t=15s
推导:
已知
V=v0+at
由两式得:
即有
三、匀变速直线运动的位移和时间的关系
讨论:上式对匀减速直线运动和初速度为零的匀加速直线运动
适用:1、当v0=0
公式变为
2、若取初速度方向为正,匀减速直线运动中,加速度取负即可
【例1】一辆汽车匀速行驶,然后以1m/s2的加速度加速行驶,从加速行驶开始,经12s行驶了180m,问:汽车开始加速时的速度是多大?
【解析】:依据题意由
得
即:汽车开始加速时的速度为9m/s。
【例2】一辆汽车以10m/s的速度匀速前进,制动后,加速度为2.5m/s2,问:3s后的位移、10s后的位移。
解:根据公式求出:
讨论x2的求法是否有问题?
2
1
at2
s
=
v
=
v0
+
a
t
v
2
–
v02
=
2
a
x
大家联立求解两式
消去t
得
此式即为:匀变速直线运动位移与速度的关系式
注意:
1、此式优点:不需计算时间t
。
2、公式中四个矢量
v、v0、a、x
要规定统一的正方向。
3、若v0
=
0
,则v
=
?
例1:一辆汽车做匀减速直线运动,初速度为15m/s,加速度大小为3m/s2,求:
(1)汽车3s末速度的大小。
(2)汽车的速度减为零所经历的时间。
(3)汽车2s内的位移。
(4)汽车第2s内的位移。
(5)汽车8s的位移。
寻找更多的方法!
注意做题的格式、用字母符号来表示物理量
15
0
t=?
v/m/s
t/s
例2:骑自行车的人以5m/s的初速度匀减地上一个斜坡,加速度的大小为0.4m/s2,斜坡长30m,骑自行车的人通过斜坡需要多少时间?
解:以初速度v0方向为正方向
由位移公式
代入数据解得:t1=10s,t2=15s
?
讨论:
把两个时间代入速度公式可算出对应的末速度:
v1=1m/s,v2=-1m/s
与实际情况不符,舍去!
答案:t=10s
根据题意得:v0
=5m/s
a=0.4m/s2
x
=30m
例题3:如图是一个物体运动的速度图线。从图中可知AB段的加速度为____m/s2,BC段的加速度为_______m/s2,CD段的加速度为____m/s2,在这段时间内物体通过的总位移为____m。
分析:AB段的加速度为:AB段物体做匀减速直线运动,所以加速度是负的。
而BC段物体做匀速直线运动,故a=0。
CD段物体做匀加速直线运动,故加速度为
物体在这段9s内运动的总位移可用三种方法计算
1、用位移公式计算
2、用图像计算
3、用x=v平t计算
答:X=17.5m
例4:
某物体从静止开始做匀加速直线运动,经过4s达到2m/s,然后以这个速度运动12s最后做匀减速直线运动,经过停下来。求物体4s
内位移大小。
x
=
1/2(
12+20
)×2
=
32
m
2
v/m/s
0
t/s
4
8
12
16
20
先作出v-t图像
例5、一质点沿ot坐标轴运动,t=0时位于坐标原点,下图为质点做直线运动的速度-时间图线,由图可知,
(1)该质点的位移随时间变化的关系式是
s=____;
(2)在20秒内,时刻t=__s时,
质点距坐标原点最远;
(3)从
t=0
到
t=
20s
内质点
的位移是多少?
通过的路程是多少?
例6、甲乙两个物体在同一直线上运动。若它们从同一位置出发,其运动的v-t图线如图所示。下列说法中正确的是:
A、甲、乙都做匀变速直线运动
B、甲比乙早出发t1时间
C、甲、乙在时刻t2相遇
D、甲的加速度的值一定
比乙大
V
t
乙
甲
t1
t2
O
v0
分析和解:甲、乙v-t图线都是直线,斜率即加速度恒定,故作匀加速直线运动,由图无法判断斜率的绝对值是否相等。由图可知,甲比乙早出发t1时间,甲、乙在时刻t2速度相等。
故选A、B
7.甲、乙两物体同时从一点向同一方向做直线运动,各自速度随时间变化的情况如图2-2-1所示,由图可知()
A.甲做匀速直线运动,乙
做初速为0的匀加速直线运动
B.开始时甲比乙快,20s后乙比甲快
C.40s末甲、乙两物体相遇
D.20s末甲、乙两物体相遇
2.3、匀变速直线运动的
位移和时间的关系
一、匀速直线运动的位移和时间的关系
v/m.s
-1
t/s
0
5
2
2.在速度-时间图象中:
图像与坐标轴所围的面积在数值上等于位移大小。
1.用公式表述:X=vt
思考
匀变速直线运动的位移是否可用
图线与坐标轴所围的面积表示
匀变速直线运动的位移和时间的关系
v/m/s
0
20
40
5
10
15
30
t/s
50
10
v/m/s
0
20
40
5
10
15
30
t/s
50
10
v/m/s
0
20
40
5
10
15
30
t/s
50
10
从图已知v0=20m/s
v=50m/s
t=15s
推导:
已知
V=v0+at
由两式得:
即有
三、匀变速直线运动的位移和时间的关系
讨论:上式对匀减速直线运动和初速度为零的匀加速直线运动
适用:1、当v0=0
公式变为
2、若取初速度方向为正,匀减速直线运动中,加速度取负即可
【例1】一辆汽车匀速行驶,然后以1m/s2的加速度加速行驶,从加速行驶开始,经12s行驶了180m,问:汽车开始加速时的速度是多大?
【解析】:依据题意由
得
即:汽车开始加速时的速度为9m/s。
【例2】一辆汽车以10m/s的速度匀速前进,制动后,加速度为2.5m/s2,问:3s后的位移、10s后的位移。
解:根据公式求出:
讨论x2的求法是否有问题?
2
1
at2
s
=
v
=
v0
+
a
t
v
2
–
v02
=
2
a
x
大家联立求解两式
消去t
得
此式即为:匀变速直线运动位移与速度的关系式
注意:
1、此式优点:不需计算时间t
。
2、公式中四个矢量
v、v0、a、x
要规定统一的正方向。
3、若v0
=
0
,则v
=
?
例1:一辆汽车做匀减速直线运动,初速度为15m/s,加速度大小为3m/s2,求:
(1)汽车3s末速度的大小。
(2)汽车的速度减为零所经历的时间。
(3)汽车2s内的位移。
(4)汽车第2s内的位移。
(5)汽车8s的位移。
寻找更多的方法!
注意做题的格式、用字母符号来表示物理量
15
0
t=?
v/m/s
t/s
例2:骑自行车的人以5m/s的初速度匀减地上一个斜坡,加速度的大小为0.4m/s2,斜坡长30m,骑自行车的人通过斜坡需要多少时间?
解:以初速度v0方向为正方向
由位移公式
代入数据解得:t1=10s,t2=15s
?
讨论:
把两个时间代入速度公式可算出对应的末速度:
v1=1m/s,v2=-1m/s
与实际情况不符,舍去!
答案:t=10s
根据题意得:v0
=5m/s
a=0.4m/s2
x
=30m
例题3:如图是一个物体运动的速度图线。从图中可知AB段的加速度为____m/s2,BC段的加速度为_______m/s2,CD段的加速度为____m/s2,在这段时间内物体通过的总位移为____m。
分析:AB段的加速度为:AB段物体做匀减速直线运动,所以加速度是负的。
而BC段物体做匀速直线运动,故a=0。
CD段物体做匀加速直线运动,故加速度为
物体在这段9s内运动的总位移可用三种方法计算
1、用位移公式计算
2、用图像计算
3、用x=v平t计算
答:X=17.5m
例4:
某物体从静止开始做匀加速直线运动,经过4s达到2m/s,然后以这个速度运动12s最后做匀减速直线运动,经过停下来。求物体4s
内位移大小。
x
=
1/2(
12+20
)×2
=
32
m
2
v/m/s
0
t/s
4
8
12
16
20
先作出v-t图像
例5、一质点沿ot坐标轴运动,t=0时位于坐标原点,下图为质点做直线运动的速度-时间图线,由图可知,
(1)该质点的位移随时间变化的关系式是
s=____;
(2)在20秒内,时刻t=__s时,
质点距坐标原点最远;
(3)从
t=0
到
t=
20s
内质点
的位移是多少?
通过的路程是多少?
例6、甲乙两个物体在同一直线上运动。若它们从同一位置出发,其运动的v-t图线如图所示。下列说法中正确的是:
A、甲、乙都做匀变速直线运动
B、甲比乙早出发t1时间
C、甲、乙在时刻t2相遇
D、甲的加速度的值一定
比乙大
V
t
乙
甲
t1
t2
O
v0
分析和解:甲、乙v-t图线都是直线,斜率即加速度恒定,故作匀加速直线运动,由图无法判断斜率的绝对值是否相等。由图可知,甲比乙早出发t1时间,甲、乙在时刻t2速度相等。
故选A、B
7.甲、乙两物体同时从一点向同一方向做直线运动,各自速度随时间变化的情况如图2-2-1所示,由图可知()
A.甲做匀速直线运动,乙
做初速为0的匀加速直线运动
B.开始时甲比乙快,20s后乙比甲快
C.40s末甲、乙两物体相遇
D.20s末甲、乙两物体相遇
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
