人教版高中物理选修3-3第八章气体达标检测(解析版)
文档属性
| 名称 | 人教版高中物理选修3-3第八章气体达标检测(解析版) | 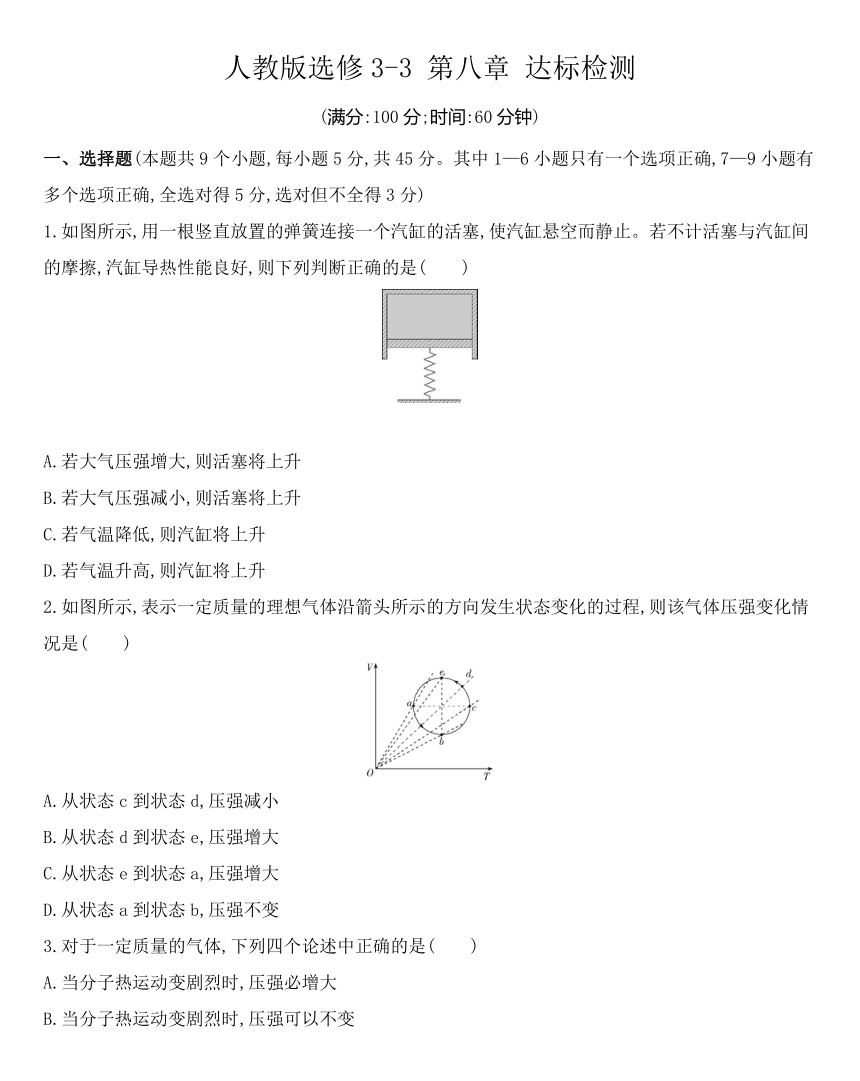 | |
| 格式 | zip | ||
| 文件大小 | 224.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-21 09:02:29 | ||
图片预览



文档简介
人教版选修3-3
第八章
达标检测
(满分:100分;时间:60分钟)
一、选择题(本题共9个小题,每小题5分,共45分。其中1—6小题只有一个选项正确,7—9小题有多个选项正确,全选对得5分,选对但不全得3分)
1.如图所示,用一根竖直放置的弹簧连接一个汽缸的活塞,使汽缸悬空而静止。若不计活塞与汽缸间的摩擦,汽缸导热性能良好,则下列判断正确的是( )
A.若大气压强增大,则活塞将上升
B.若大气压强减小,则活塞将上升
C.若气温降低,则汽缸将上升
D.若气温升高,则汽缸将上升
2.如图所示,表示一定质量的理想气体沿箭头所示的方向发生状态变化的过程,则该气体压强变化情况是( )
A.从状态c到状态d,压强减小
B.从状态d到状态e,压强增大
C.从状态e到状态a,压强增大
D.从状态a到状态b,压强不变
3.对于一定质量的气体,下列四个论述中正确的是( )
A.当分子热运动变剧烈时,压强必增大
B.当分子热运动变剧烈时,压强可以不变
C.当分子间平均距离变大时,压强必变大
D.当分子间平均距离变大时,压强必变小
4.一定质量的气体,从初态(p0、V0、T0)先经等压变化使温度上升到T0,再经等容变化使压强减小到p0,则气体最后状态的参量为( )
A.p0、V0、T0
B.p0、V0、T0
C.p0、V0、T0
D.p0、V0、T0
5.如图所示是一定质量的理想气体的p-V图线,若其状态由A→B→C→A,且A→B等容,B→C等压,C→A等温,则气体在A、B、C三个状态时( )
A.单位体积内气体的分子数nA=nB=nC
B.气体分子的平均速率vA>vB>vC
C.气体分子在单位时间内对器壁单位面积的平均作用力FA>FB,FB=FC
D.气体分子在单位时间内对器壁单位面积碰撞的次数NA>NB,NC>NA
6.一只两用活塞气筒的原理如图所示(打气时如图甲,抽气时如图乙),其筒内体积为V0,现将它与另一只容积为V的容器相连接,气筒和容器内的空气压强为p0,已知气筒和容器导热性能良好,当分别作为打气筒和抽气筒时,活塞工作n次后,在上述两种情况下,容器内的气体压强分别为( )
A.np0,p0
B.p0,
p0
C.(1+)np0,(1+)np0
D.(1+)p0,()np0
7.如图所示,在光滑的水平面上,有一个内外壁都光滑的汽缸,汽缸的质量为M,汽缸内有一质量为m(mA.p1>p2
B.p1C.V1>V2
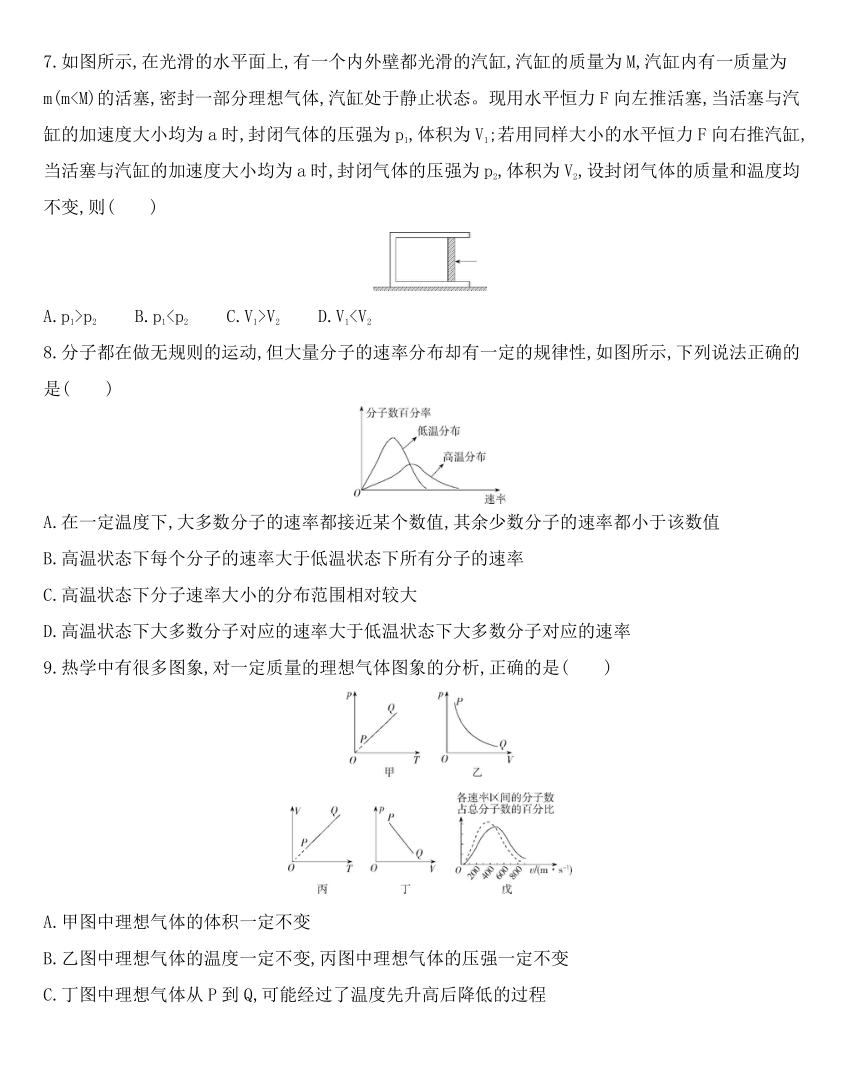
D.V18.分子都在做无规则的运动,但大量分子的速率分布却有一定的规律性,如图所示,下列说法正确的是( )
A.在一定温度下,大多数分子的速率都接近某个数值,其余少数分子的速率都小于该数值
B.高温状态下每个分子的速率大于低温状态下所有分子的速率
C.高温状态下分子速率大小的分布范围相对较大
D.高温状态下大多数分子对应的速率大于低温状态下大多数分子对应的速率
9.热学中有很多图象,对一定质量的理想气体图象的分析,正确的是( )
A.甲图中理想气体的体积一定不变
B.乙图中理想气体的温度一定不变,丙图中理想气体的压强一定不变
C.丁图中理想气体从P到Q,可能经过了温度先升高后降低的过程
D.戊图中实线对应的气体温度高于虚线对应的气体温度
二、非选择题(本题共5小题,共55分)
10.(10分)如图所示,在玻璃筒内装入一些塑料小球,这些小球代表气体分子。在小球上面放一个轻质活塞,用电动机带动玻璃筒底部的振动器使小球无规则运动。当电动机启动后,活塞受到小球的撞击,悬浮在一定的高度。增加电动机的转速,活塞高度将 ,保持电动机的转速不变,减少塑料小球的数目,活塞高度将 。(填“增大”“减小”或“不变”)?
11.(10分)如图所示为一种测定“肺活量”(标准大气压下人一次呼出气体的体积)的装置,A为开口薄壁圆筒,排尽其中的空气,倒扣在水中。测量时,被测者尽力吸尽空气,再通过B管用力将气体吹入A中,使A浮起。设整个过程中呼出气体的温度保持不变。
(1)呼出气体的分子热运动的平均动能 (填“增大”“减小”或“不变”)。?
(2)设圆筒A的横截面积为S,大气压强为p0,水的密度为ρ,桶底浮出水面的高度为h,桶内外水面的高度差为Δh,被测者的“肺活量”,即V0= 。?
12.(10分)一定质量的理想气体由状态A经状态B变为状态C,其体积V与热力学温度T的关系图象如图所示,已知气体在状态A时的压强pA=p0,线段AB与V轴平行,BC的延长线过原点。求:
(1)气体在状态B时的压强pB;
(2)气体在状态C时的压强pC和温度TC;
(3)画出全过程的p-V图象。
13.(10分)如图所示为一竖直放置、上粗下细且上端开口的薄壁玻璃管,上部和下部的横截面积之比为2∶1,上管足够长,下管长度l=34
cm,在管内用长度h=4
cm的水银柱封闭一定质量的气体,气柱长度l1=20
cm。大气压强p0=76
cmHg,气体初始温度T1=300
K。
(1)若缓慢升高气体温度,使水银上表面到达粗管和细管交界处,求此时的温度T2;
(2)继续缓慢升高温度至水银恰好全部进入粗管,求此时的温度T3。
14.(15分)如图所示,在一导热性能良好开口向上的汽缸,用一质量不计、横截面积为S的活塞封闭有体积为V0的理想气体,已知外界大气压强为p0,环境温度为T0,活塞与汽缸之间的摩擦不计,现在活塞上面轻放一质量为m的物块,使活塞缓慢下移,最终活塞静止在某一位置,重力加速度为g,则:
(1)当活塞静止时,活塞与汽缸底端的距离是多少?
(2)如果将物块拿掉,要活塞保持在(1)问所处的位置,环境温度需要变为多少?
答案
一、选择题
1.D 以活塞与汽缸整体为研究对象,受到重力和弹簧的弹力作用,且弹簧的弹力等于重力,故外界大气压增大或减小时,弹簧压缩量不变,活塞将静止不动,故A、B错误;若气温升高,弹簧压缩量不变,则由=可知,气体的体积增大,汽缸将上升,选项C
错误,D正确。
2.A 在V
-T图象中,等压线是过坐标原点的直线。由理想气体状态方程知=,可见,当压强增大,等压线的斜率k==变小。由题图可确定pa3.B 分子热运动变剧烈,表明气体温度升高,分子平均动能增大,但不知气体分子的密集程度怎么变化,故压强的变化趋势不明确,故A错,B对。分子的平均距离变大,表明气体分子的密集程度变小,但因不知此时分子的平均动能怎么变化,故气体的压强不知怎么变化,故C、D错。
4.B 由盖—吕萨克定律=C可知,温度上升到T0时体积增大到V0,由查理定律=可知,压强减小到p0时,温度变成T0,故最后状态的参量为:p0、V0、T0,选项B正确。
5.C 由题图可知B→C气体的体积增大,密度减小,故选项A错。C→A为等温变化,分子平均速率vA=vC,故选项B错。关于气体分子在单位时间内对器壁单位面积的平均作用力,B→C为等压过程,pB=pC,FB=FC,由题图知,pA>pB,则FA>FB,故C选项正确。A→B为等容降压过程,分子密集程度不变,温度降低,NA>NB,C→A为等温压缩过程,温度不变,分子密集程度增大,应有NA>NC,故D选项错误。
6.D 打气时,活塞每推动一次,把体积为V0、压强为p0的气体推入容器内,若活塞工作n次,就是把压强为p0、体积为nV0的气体推入容器内,容器内原来有压强为p0、体积为V的气体,根据玻意耳定律得:p0(V+nV0)=p'V,所以p'=p0=(1+n)p0;抽气时,活塞每拉动一次,把容器中的气体的体积从V膨胀为V+V0,而容器中的气体压强就要减小,活塞推动时,将抽气筒中的V0气体排出,而再次拉动活塞时,将容器中剩余的气体从V又膨胀到V+V0,容器内的压强继续减小,根据玻意耳定律得,第一次抽气:p0V=p1(V+V0),则p1=p0,第二次抽气:p1V=p2(V+V0),则p2=p1=()2p0,则第n次抽气后:pn=()np0,故D正确。
7.AD 向左推时,对于汽缸:p1S-p0S=Ma,解得p1=p0+;向右推时,对于活塞:p2S-p0S=ma,解得p2=p0+,可见p1>p2,由玻意耳定律得V18.CD 由题中图象可知,在一定温度下,大多数分子的速率接近某个数值,其余少数分子的速率有的大于该值、有的小于该值,故选项A错误。高温状态下每个分子的速率并非都大于低温状态下所有分子的速率,选项B错误。由题中图象可看出,高温状态下分子速率大小的分布范围相对较大,且高温状态下大多数分子对应的速率大于低温状态下大多数分子对应的速率,选项C、D正确。
9.ACD 题图甲中,p-T图线是过原点的直线,则理想气体的体积一定不变,选项A正确;题图乙中图线不一定是双曲线,则题图乙中理想气体的温度不一定不变;题图丙中V-T图线是过原点的直线,理想气体的压强一定不变,选项B错误;由题图丁可知,从P到Q的过程中,pV乘积先增加后减小,则温度先升高,后降低,故C正确;温度升高时,速率分布最大的区间将向速率增大处移动,所以气体由虚线状态变成实线状态时,温度升高,实线对应的温度一定高于虚线对应的温度,故D正确。
二、非选择题
10.答案 增大 减小
解析 增大转速,小球(气体分子)运动剧烈程度增加,单位时间内撞击的次数和力度均增大,所以产生的压强增大,活塞高度会增大;保持转速不变,即小球(气体分子)运动剧烈程度不变,但是减少小球数目,单位时间撞击次数减少,压强变小,活塞高度将减小。
11.答案 (1)不变 (2)
解析 (1)由于温度是分子平均动能大小的标志,因为气体温度不变,所以分子平均动能不变。
(2)设A中气体压强为p,该部分气体在标准大气压下的体积为V0,由于整个过程中温度不变,由玻意耳定律可得:p0V0=pV,即p0V0=(p0+ρgΔh)(h+Δh)S,被测者的肺活量V0=。
12.答案 (1)p0 (2)p0 T0 (3)见解析
解析 (1)A→B为等温变化,由玻意耳定律得,pAV0=pB·2V0
解得pB=pA=p0
(2)B→C为等压变化,则pC=pB=p0
由=得TC=T0
(3)如图所示
13.答案 (1)450
K (2)497.25
K
解析 (1)从初态到水银上表面到达粗管和细管交界处,压强不变,设细管口的横截面积为S。
初态:p1=p0+ph=80
cmHg,V1=l1S,T1=300
K
末态:p2=p0+ph=80
cmHg,V2=(l-h)S
由盖—吕萨克定律:=
解得:T2=450
K
(2)水银恰好全部进入粗管时,水银高度为h'=2
cm
此时:p3=p0+ph'=78
cmHg,V3=lS
由理想气体状态方程:=
解得:T3=497.25
K
14.答案 (1) (2)
解析 (1)放上物块并稳定后,由平衡条件得:
pS=p0S+mg
达到稳定过程,根据玻意耳定律得:p0V0=pSx
解得:x=
(2)拿掉物块后要保持活塞位置不变,即气体体积不变,根据查理定律得:=
解得:T=
第八章
达标检测
(满分:100分;时间:60分钟)
一、选择题(本题共9个小题,每小题5分,共45分。其中1—6小题只有一个选项正确,7—9小题有多个选项正确,全选对得5分,选对但不全得3分)
1.如图所示,用一根竖直放置的弹簧连接一个汽缸的活塞,使汽缸悬空而静止。若不计活塞与汽缸间的摩擦,汽缸导热性能良好,则下列判断正确的是( )
A.若大气压强增大,则活塞将上升
B.若大气压强减小,则活塞将上升
C.若气温降低,则汽缸将上升
D.若气温升高,则汽缸将上升
2.如图所示,表示一定质量的理想气体沿箭头所示的方向发生状态变化的过程,则该气体压强变化情况是( )
A.从状态c到状态d,压强减小
B.从状态d到状态e,压强增大
C.从状态e到状态a,压强增大
D.从状态a到状态b,压强不变
3.对于一定质量的气体,下列四个论述中正确的是( )
A.当分子热运动变剧烈时,压强必增大
B.当分子热运动变剧烈时,压强可以不变
C.当分子间平均距离变大时,压强必变大
D.当分子间平均距离变大时,压强必变小
4.一定质量的气体,从初态(p0、V0、T0)先经等压变化使温度上升到T0,再经等容变化使压强减小到p0,则气体最后状态的参量为( )
A.p0、V0、T0
B.p0、V0、T0
C.p0、V0、T0
D.p0、V0、T0
5.如图所示是一定质量的理想气体的p-V图线,若其状态由A→B→C→A,且A→B等容,B→C等压,C→A等温,则气体在A、B、C三个状态时( )
A.单位体积内气体的分子数nA=nB=nC
B.气体分子的平均速率vA>vB>vC
C.气体分子在单位时间内对器壁单位面积的平均作用力FA>FB,FB=FC
D.气体分子在单位时间内对器壁单位面积碰撞的次数NA>NB,NC>NA
6.一只两用活塞气筒的原理如图所示(打气时如图甲,抽气时如图乙),其筒内体积为V0,现将它与另一只容积为V的容器相连接,气筒和容器内的空气压强为p0,已知气筒和容器导热性能良好,当分别作为打气筒和抽气筒时,活塞工作n次后,在上述两种情况下,容器内的气体压强分别为( )
A.np0,p0
B.p0,
p0
C.(1+)np0,(1+)np0
D.(1+)p0,()np0
7.如图所示,在光滑的水平面上,有一个内外壁都光滑的汽缸,汽缸的质量为M,汽缸内有一质量为m(m
B.p1
D.V1
A.在一定温度下,大多数分子的速率都接近某个数值,其余少数分子的速率都小于该数值
B.高温状态下每个分子的速率大于低温状态下所有分子的速率
C.高温状态下分子速率大小的分布范围相对较大
D.高温状态下大多数分子对应的速率大于低温状态下大多数分子对应的速率
9.热学中有很多图象,对一定质量的理想气体图象的分析,正确的是( )
A.甲图中理想气体的体积一定不变
B.乙图中理想气体的温度一定不变,丙图中理想气体的压强一定不变
C.丁图中理想气体从P到Q,可能经过了温度先升高后降低的过程
D.戊图中实线对应的气体温度高于虚线对应的气体温度
二、非选择题(本题共5小题,共55分)
10.(10分)如图所示,在玻璃筒内装入一些塑料小球,这些小球代表气体分子。在小球上面放一个轻质活塞,用电动机带动玻璃筒底部的振动器使小球无规则运动。当电动机启动后,活塞受到小球的撞击,悬浮在一定的高度。增加电动机的转速,活塞高度将 ,保持电动机的转速不变,减少塑料小球的数目,活塞高度将 。(填“增大”“减小”或“不变”)?
11.(10分)如图所示为一种测定“肺活量”(标准大气压下人一次呼出气体的体积)的装置,A为开口薄壁圆筒,排尽其中的空气,倒扣在水中。测量时,被测者尽力吸尽空气,再通过B管用力将气体吹入A中,使A浮起。设整个过程中呼出气体的温度保持不变。
(1)呼出气体的分子热运动的平均动能 (填“增大”“减小”或“不变”)。?
(2)设圆筒A的横截面积为S,大气压强为p0,水的密度为ρ,桶底浮出水面的高度为h,桶内外水面的高度差为Δh,被测者的“肺活量”,即V0= 。?
12.(10分)一定质量的理想气体由状态A经状态B变为状态C,其体积V与热力学温度T的关系图象如图所示,已知气体在状态A时的压强pA=p0,线段AB与V轴平行,BC的延长线过原点。求:
(1)气体在状态B时的压强pB;
(2)气体在状态C时的压强pC和温度TC;
(3)画出全过程的p-V图象。
13.(10分)如图所示为一竖直放置、上粗下细且上端开口的薄壁玻璃管,上部和下部的横截面积之比为2∶1,上管足够长,下管长度l=34
cm,在管内用长度h=4
cm的水银柱封闭一定质量的气体,气柱长度l1=20
cm。大气压强p0=76
cmHg,气体初始温度T1=300
K。
(1)若缓慢升高气体温度,使水银上表面到达粗管和细管交界处,求此时的温度T2;
(2)继续缓慢升高温度至水银恰好全部进入粗管,求此时的温度T3。
14.(15分)如图所示,在一导热性能良好开口向上的汽缸,用一质量不计、横截面积为S的活塞封闭有体积为V0的理想气体,已知外界大气压强为p0,环境温度为T0,活塞与汽缸之间的摩擦不计,现在活塞上面轻放一质量为m的物块,使活塞缓慢下移,最终活塞静止在某一位置,重力加速度为g,则:
(1)当活塞静止时,活塞与汽缸底端的距离是多少?
(2)如果将物块拿掉,要活塞保持在(1)问所处的位置,环境温度需要变为多少?
答案
一、选择题
1.D 以活塞与汽缸整体为研究对象,受到重力和弹簧的弹力作用,且弹簧的弹力等于重力,故外界大气压增大或减小时,弹簧压缩量不变,活塞将静止不动,故A、B错误;若气温升高,弹簧压缩量不变,则由=可知,气体的体积增大,汽缸将上升,选项C
错误,D正确。
2.A 在V
-T图象中,等压线是过坐标原点的直线。由理想气体状态方程知=,可见,当压强增大,等压线的斜率k==变小。由题图可确定pa
4.B 由盖—吕萨克定律=C可知,温度上升到T0时体积增大到V0,由查理定律=可知,压强减小到p0时,温度变成T0,故最后状态的参量为:p0、V0、T0,选项B正确。
5.C 由题图可知B→C气体的体积增大,密度减小,故选项A错。C→A为等温变化,分子平均速率vA=vC,故选项B错。关于气体分子在单位时间内对器壁单位面积的平均作用力,B→C为等压过程,pB=pC,FB=FC,由题图知,pA>pB,则FA>FB,故C选项正确。A→B为等容降压过程,分子密集程度不变,温度降低,NA>NB,C→A为等温压缩过程,温度不变,分子密集程度增大,应有NA>NC,故D选项错误。
6.D 打气时,活塞每推动一次,把体积为V0、压强为p0的气体推入容器内,若活塞工作n次,就是把压强为p0、体积为nV0的气体推入容器内,容器内原来有压强为p0、体积为V的气体,根据玻意耳定律得:p0(V+nV0)=p'V,所以p'=p0=(1+n)p0;抽气时,活塞每拉动一次,把容器中的气体的体积从V膨胀为V+V0,而容器中的气体压强就要减小,活塞推动时,将抽气筒中的V0气体排出,而再次拉动活塞时,将容器中剩余的气体从V又膨胀到V+V0,容器内的压强继续减小,根据玻意耳定律得,第一次抽气:p0V=p1(V+V0),则p1=p0,第二次抽气:p1V=p2(V+V0),则p2=p1=()2p0,则第n次抽气后:pn=()np0,故D正确。
7.AD 向左推时,对于汽缸:p1S-p0S=Ma,解得p1=p0+;向右推时,对于活塞:p2S-p0S=ma,解得p2=p0+,可见p1>p2,由玻意耳定律得V1
9.ACD 题图甲中,p-T图线是过原点的直线,则理想气体的体积一定不变,选项A正确;题图乙中图线不一定是双曲线,则题图乙中理想气体的温度不一定不变;题图丙中V-T图线是过原点的直线,理想气体的压强一定不变,选项B错误;由题图丁可知,从P到Q的过程中,pV乘积先增加后减小,则温度先升高,后降低,故C正确;温度升高时,速率分布最大的区间将向速率增大处移动,所以气体由虚线状态变成实线状态时,温度升高,实线对应的温度一定高于虚线对应的温度,故D正确。
二、非选择题
10.答案 增大 减小
解析 增大转速,小球(气体分子)运动剧烈程度增加,单位时间内撞击的次数和力度均增大,所以产生的压强增大,活塞高度会增大;保持转速不变,即小球(气体分子)运动剧烈程度不变,但是减少小球数目,单位时间撞击次数减少,压强变小,活塞高度将减小。
11.答案 (1)不变 (2)
解析 (1)由于温度是分子平均动能大小的标志,因为气体温度不变,所以分子平均动能不变。
(2)设A中气体压强为p,该部分气体在标准大气压下的体积为V0,由于整个过程中温度不变,由玻意耳定律可得:p0V0=pV,即p0V0=(p0+ρgΔh)(h+Δh)S,被测者的肺活量V0=。
12.答案 (1)p0 (2)p0 T0 (3)见解析
解析 (1)A→B为等温变化,由玻意耳定律得,pAV0=pB·2V0
解得pB=pA=p0
(2)B→C为等压变化,则pC=pB=p0
由=得TC=T0
(3)如图所示
13.答案 (1)450
K (2)497.25
K
解析 (1)从初态到水银上表面到达粗管和细管交界处,压强不变,设细管口的横截面积为S。
初态:p1=p0+ph=80
cmHg,V1=l1S,T1=300
K
末态:p2=p0+ph=80
cmHg,V2=(l-h)S
由盖—吕萨克定律:=
解得:T2=450
K
(2)水银恰好全部进入粗管时,水银高度为h'=2
cm
此时:p3=p0+ph'=78
cmHg,V3=lS
由理想气体状态方程:=
解得:T3=497.25
K
14.答案 (1) (2)
解析 (1)放上物块并稳定后,由平衡条件得:
pS=p0S+mg
达到稳定过程,根据玻意耳定律得:p0V0=pSx
解得:x=
(2)拿掉物块后要保持活塞位置不变,即气体体积不变,根据查理定律得:=
解得:T=
