高中物理必修第三册知识点归纳(附同步练习)9.4静电的防止与利用-人教版(2019)
文档属性
| 名称 | 高中物理必修第三册知识点归纳(附同步练习)9.4静电的防止与利用-人教版(2019) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-21 10:30:04 | ||
图片预览




文档简介
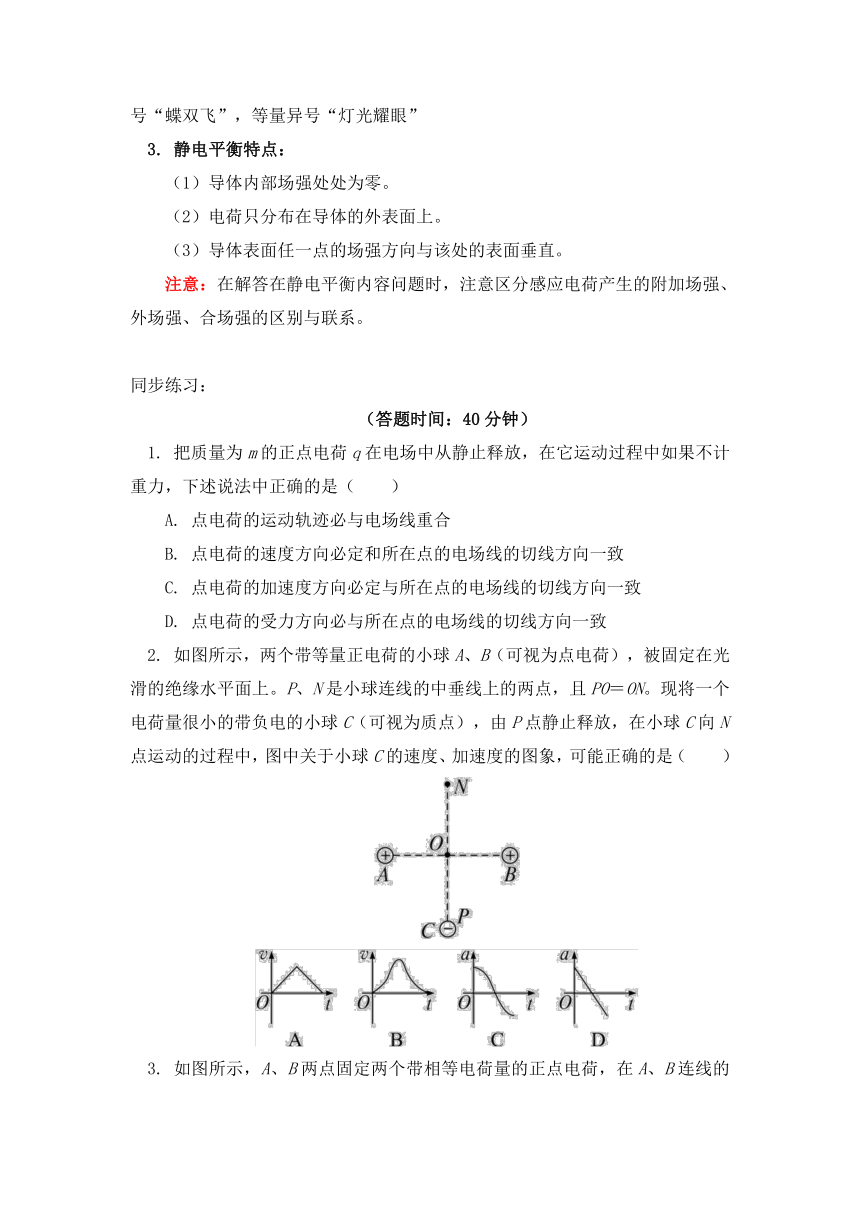
静电的防止与利用
重难点
题型
分值
重点
各种电场的电场线分布
选择
计算
6-8分
难点
利用电场线解决问题
知识脉络:
知识精讲:
电场线
1. 定义
电场线是画在电场中的一条条有方向的曲线,曲线上每一点的切线方向表示该点的电场强度方向。如图所示。
2. 特点
电场线是由法拉第首先引入和使用的,是描述电场的重要工具。
(1)电场线从正电荷或无限远处出发,终止于无限远处或负电荷,不是闭合曲线。
(2)电场线在电场中不相交,不闭合。若电场线在某点相交,则交点相对两条电场线有两个切线方向,该点的电场强度方向有两个,这是不可能的。
(3)在同一电场中,电场强度较大的地方电场线较密集,电场强度较小的地方电场线较稀疏,因此可以用电场线的疏密来表示电场强度的相对大小。如图中,由于A点处的电场线比B点处的密,可知EA>EB。
(4)电场线是人为画出的,是为了形象描述电场而假想的一些线(实际并不存在)。
3. 几种常见电场的电场线分布特征
(1)孤立的点电荷电场:
a. 离点电荷越近,电场线越密,场强越大
b. 以点电荷为球心作个球面,电场线处处与球面垂直,在此球面上场强大小处处相等,方向不同。
(2)匀强电场的电场线是平行等距的直线。
注意:常见电场线的记忆:“光芒四射”正电荷,“万箭穿心”负电荷,等量同号“蝶双飞”,等量异号“灯光耀眼”
4. 两种等量点电荷的电场分析
等量异种点电荷
等量同种点电荷
电场线分布图
电荷连线上的电场强度
沿连线先变小后变大
O点最小,但不为零
O点为零
中垂线上的电场强度
O点最大,向外逐渐减小
O点最小,向外先变大后变小
关于O点对称位置的电场强度
A与A′、B与B′、C与C′
等大同向
等大反向
5. 电场线的应用
判断电场强度的大小
电场线密处电场强度大,电场线疏处电场强度小,进而可判断电荷受力大小和加速度的大小
判断电场力的方向
正电荷的受力方向和电场线在该点切线方向相同,负电荷的受力方向和电场线在该点切线方向相反
核心知识二:
静电平衡
1. 静电平衡
(1)定义:导体中没有电荷定向移动的状态。
(2)特点:
①导体内部场强处处为零。
②电荷只分布在导体的外表面上。
③导体表面任一点的场强方向与该处的表面垂直。
2. 静电平衡的分析
(1)自由电荷的移动:导体刚放入电场E0中的瞬间,导体中的自由电荷受电场力F的作用,产生定向运动(如图甲),同时在导体中产生一个与E0方向相反的附加电场E′(如图乙)。这两个电场叠加,使导体内部电场E减弱。
(2)电场叠加:当E0=E′时,导体内合场强为零,即E=0(如图丙),自由电荷受合力也为零,这时导体中无电荷定向移动,即达到了静电平衡状态。
(3)结论:处于静电平衡的导体内部电场强度处处为零。导体内部场强为零指的是外部电场和附加电场的合场强为零,其效果相互抵消。
3. 静电屏蔽
当中空的导体达到静电平衡时,内部无电场,因而导体的外壳会对其内部起屏蔽作用,使它内部不受电场影响的现象。
归纳总结:
1. 电场线特点:
(1)电场线实际不存在。
(2)电场线的切线方向——电场强度的方向;电场线的疏密程度——电场强度的大小,电场线越密的地方,电场强度越大,电场线越稀的地方,电场强度越小。
注意:仅由一条电场线不能判定电场强度的大小。
如图所示是一条水平向右的电场线,我们只能确定三点的电场强度方向都为水平向右,但不能判断三点电场强度的大小。
①若该电场线是左边某正点电荷发出的,则有Ea>Eb>Ec;
②若该电场线是右边某负点电荷发出的,则有Ea③若该电场线是某匀强电场的电场线中的一条,则有Ea=Eb=Ec。
(3)电场线在电场中不相交,不闭合。
2. 常见电场线的记忆:“光芒四射”正电荷,“万箭穿心”负电荷,等量同号“蝶双飞”,等量异号“灯光耀眼”
3. 静电平衡特点:
(1)导体内部场强处处为零。
(2)电荷只分布在导体的外表面上。
(3)导体表面任一点的场强方向与该处的表面垂直。
注意:在解答在静电平衡内容问题时,注意区分感应电荷产生的附加场强、外场强、合场强的区别与联系。
同步练习:
(答题时间:40分钟)
1. 把质量为m的正点电荷q在电场中从静止释放,在它运动过程中如果不计重力,下述说法中正确的是( )
A. 点电荷的运动轨迹必与电场线重合
B. 点电荷的速度方向必定和所在点的电场线的切线方向一致
C. 点电荷的加速度方向必定与所在点的电场线的切线方向一致
D. 点电荷的受力方向必与所在点的电场线的切线方向一致
2. 如图所示,两个带等量正电荷的小球A、B(可视为点电荷),被固定在光滑的绝缘水平面上。P、N是小球连线的中垂线上的两点,且PO=ON。现将一个电荷量很小的带负电的小球C(可视为质点),由P点静止释放,在小球C向N点运动的过程中,图中关于小球C的速度、加速度的图象,可能正确的是( )
3. 如图所示,A、B两点固定两个带相等电荷量的正点电荷,在A、B连线的中点C处放一点电荷(不计重力)。若给该点电荷一个初速度v0,v0方向与A、B连线垂直,则该点电荷的运动情况是( )
A. 如果C处的电荷为正电荷,则它可能做往复直线运动
B. 如果C处的电荷为负电荷,则它可能做往复直线运动
C. 如果C处的电荷为正电荷,则它做加速度先增大后减小、速度不断增大的直线运动
D. 如果C处的电荷为负电荷,则它做加速度先增大后减小、速度不断增大的直线运动
4. 将悬挂在细线上的带正电的小球A放在不带电的金属空心球C内(不与球接触),另有一个悬挂在细线上的带负电的小于B向C靠近,如图所示,于是有( )
A. A向左偏离竖直方向,B向右偏离竖直方向
B. A的位置不变,B向右偏离竖直方向
C. A向左偏离竖直方向,B的位置不变
D. A和B的位置都不变
5. 如图所示是某静电场的一部分电场线分布情况,下列说法中正确的是( )
A. 这个电场可能是负点电荷的电场
B. 点电荷q在A点处受到的静电力比在B点处受到的静电力大
C. 点电荷q在A点处的瞬时加速度比在B点处的瞬时加速度小(不计重力)
D. 负电荷在B点处受到的静电力的方向沿B点切线方向
6. 有一接地的导体球壳,如图所示,球心处放一点电荷q,达到静电平衡时,则( )
A. q的电量变化时,球壳外电场随之改变
B. q在球壳外产生的电场强度为零
C. 球壳内、外表面的电荷在壳外的合场强为零
D. q与球壳内表面的电荷在壳外的合场强为零
*7. y轴上放置一块不带电的无限大接地金属板,现在x轴上的(L,0)点放一电荷量为q的正点电荷,它们之间的电场线分布如图甲所示。两个相距为2L的电荷量均为q的等量异种点电荷之间的电场线分布如图乙所示。某同学经过探究之后发现图甲所示的电场线分布与图乙中虚线(两点电荷连线的中垂线)右侧的电场线分布相同,求P(2L,0)点的电场强度的大小。
*8. 如图所示,在一足够大的空间内存在着水平向右的匀强电场,电场强度大小E=3.0×104 N/C。有一个质量m=4. 0×10-3 kg的带电小球,用绝缘轻细线悬挂起来,静止时细线偏离竖直方向的夹角θ=37°. 取g=10 m/s2,sin 37°=0. 60,cos 37°=0. 80,不计空气阻力的作用。
(1)求小球所带的电荷量及电性;
(2)如果将细线轻轻剪断,求细线剪断后,小球运动的加速度大小;
(3)从剪断细线开始经过时间t=0. 20 s,求这一段时间内小球电场力做的功。
答案:
1. 【答案】CD
【解析】正点电荷q由静止释放,如果电场线为直线,电荷将沿电场线运动,但电场线如果是曲线,电荷一定不沿电场线运动(因为如果沿电场线运动,其速度方向与受力方向重合,不符合曲线运动的条件),故A选项不正确;由于点电荷做曲线运动时,其速度方向与静电力方向不再一致(初始时刻除外),故B选项不正确;而点电荷的加速度方向,也即电荷所受静电力方向必与该点电场强度方向一致,即与所在点的电场线的切线方向一致,故C、D选项正确。
2. 【答案】BC
【解析】小球C向N点运动过程中,受到的静电力是变力,在中点O时受力为零,所以速度—时间图象不是直线,A错误,B可能;由牛顿第二定律结合库仑定律可知C可能,D错误。
3. 【答案】BC
【解析】带相等电荷量的两个正电荷中垂线上的场强变化情况是,C点合场强为零,从C向外电强度先变大后变小,电场强度方向向外。因此如果C处放点电荷为正电荷,则释放后点电荷先做加速度逐渐增大的加速运动,然后再做加速度逐渐减小的加速运动,故C正确;如果C处所放点电荷为负电荷,则点电荷先做加速度增大的减速运动,再做加速度减小的减速运动,当速度减为零时再向下加速,到C点后再向下减速,速度减为零后,再向上加速,做往复直线运动,故B正确。
4. 【答案】B
【解析】考虑B对A的作用时,A处在球壳C内,球壳C会对其内的A有屏蔽作用,使A不受B的作用。A通过静电感应使C的内、外壳分别带负电荷和正电荷,从而知道B受C外壳正电荷吸引,所以B往右偏离竖直方向,故B正确。
5. 【答案】B
【解析】电场线的疏密反映了电场强度的大小,而加速度的大小关键是看静电力的大小。判断A、B两处电场线的疏密是解答本题的关键。负点电荷的电场线是从四周无限远处不同方向指向负点电荷的直线,故A错;电场线越密的地方电场强度越大,由图知FA>FB,故B正确;由a=false知,a∝F,而F∝E,EA>EB,所以aA>aB,故C错;负电荷在B点受到的静电力的方向与B点电场强度的方向相反,故D错误。故选B。
6. 【答案】D
【解析】当导体球壳接地时,壳内电荷在壳外表面所产生的感应电荷流入大地,这时壳内电荷与壳内表面的感应电荷在壳内壁以外(包含导体壳层)任一点的合场强为零。故选项D正确。
7. 【答案】false
【解析】图甲所示的电场线分布与图乙中虚线(两点电荷连线的中垂线)右侧的电场线分布相同,因此P(2L,0)点的电场强度与乙图中正、负电荷连线上正电荷右侧L处电场强度相同,此处有两个电场,正电荷电场E1=false,方向向右,负电荷的电场E2=false,方向向左,两个电场的合电场强度就是P点电场强度E=E1-E2=false。
8. 【答案】(1)1. 0×10-6 C 正电荷 (2)12. 5 m/s2 (3)4. 5×10-3 J
【解析】(1)小球受到重力mg、电场力F和细线的拉力T的作用,
如图所示,由共点力平衡条件有:
F=qE=mgtan θ
解得:q=false =1. 0×10-6 C
电场力的方向与电场强度的方向相同,故小球所带电荷为正电荷。
(2)剪断细线后,小球做匀加速直线运动,设其加速度为a,由牛顿第二定律有:false=ma
解得:a=false=12. 5 m/s2.
(3)在t=0. 20 s的时间内,小球的位移为:
l=falseat2=0. 25 m
小球运动过程中,电场力做的功为:
W=qElsin θ=mglsin θtan θ=4. 5×10-3 J
重难点
题型
分值
重点
各种电场的电场线分布
选择
计算
6-8分
难点
利用电场线解决问题
知识脉络:
知识精讲:
电场线
1. 定义
电场线是画在电场中的一条条有方向的曲线,曲线上每一点的切线方向表示该点的电场强度方向。如图所示。
2. 特点
电场线是由法拉第首先引入和使用的,是描述电场的重要工具。
(1)电场线从正电荷或无限远处出发,终止于无限远处或负电荷,不是闭合曲线。
(2)电场线在电场中不相交,不闭合。若电场线在某点相交,则交点相对两条电场线有两个切线方向,该点的电场强度方向有两个,这是不可能的。
(3)在同一电场中,电场强度较大的地方电场线较密集,电场强度较小的地方电场线较稀疏,因此可以用电场线的疏密来表示电场强度的相对大小。如图中,由于A点处的电场线比B点处的密,可知EA>EB。
(4)电场线是人为画出的,是为了形象描述电场而假想的一些线(实际并不存在)。
3. 几种常见电场的电场线分布特征
(1)孤立的点电荷电场:
a. 离点电荷越近,电场线越密,场强越大
b. 以点电荷为球心作个球面,电场线处处与球面垂直,在此球面上场强大小处处相等,方向不同。
(2)匀强电场的电场线是平行等距的直线。
注意:常见电场线的记忆:“光芒四射”正电荷,“万箭穿心”负电荷,等量同号“蝶双飞”,等量异号“灯光耀眼”
4. 两种等量点电荷的电场分析
等量异种点电荷
等量同种点电荷
电场线分布图
电荷连线上的电场强度
沿连线先变小后变大
O点最小,但不为零
O点为零
中垂线上的电场强度
O点最大,向外逐渐减小
O点最小,向外先变大后变小
关于O点对称位置的电场强度
A与A′、B与B′、C与C′
等大同向
等大反向
5. 电场线的应用
判断电场强度的大小
电场线密处电场强度大,电场线疏处电场强度小,进而可判断电荷受力大小和加速度的大小
判断电场力的方向
正电荷的受力方向和电场线在该点切线方向相同,负电荷的受力方向和电场线在该点切线方向相反
核心知识二:
静电平衡
1. 静电平衡
(1)定义:导体中没有电荷定向移动的状态。
(2)特点:
①导体内部场强处处为零。
②电荷只分布在导体的外表面上。
③导体表面任一点的场强方向与该处的表面垂直。
2. 静电平衡的分析
(1)自由电荷的移动:导体刚放入电场E0中的瞬间,导体中的自由电荷受电场力F的作用,产生定向运动(如图甲),同时在导体中产生一个与E0方向相反的附加电场E′(如图乙)。这两个电场叠加,使导体内部电场E减弱。
(2)电场叠加:当E0=E′时,导体内合场强为零,即E=0(如图丙),自由电荷受合力也为零,这时导体中无电荷定向移动,即达到了静电平衡状态。
(3)结论:处于静电平衡的导体内部电场强度处处为零。导体内部场强为零指的是外部电场和附加电场的合场强为零,其效果相互抵消。
3. 静电屏蔽
当中空的导体达到静电平衡时,内部无电场,因而导体的外壳会对其内部起屏蔽作用,使它内部不受电场影响的现象。
归纳总结:
1. 电场线特点:
(1)电场线实际不存在。
(2)电场线的切线方向——电场强度的方向;电场线的疏密程度——电场强度的大小,电场线越密的地方,电场强度越大,电场线越稀的地方,电场强度越小。
注意:仅由一条电场线不能判定电场强度的大小。
如图所示是一条水平向右的电场线,我们只能确定三点的电场强度方向都为水平向右,但不能判断三点电场强度的大小。
①若该电场线是左边某正点电荷发出的,则有Ea>Eb>Ec;
②若该电场线是右边某负点电荷发出的,则有Ea
(3)电场线在电场中不相交,不闭合。
2. 常见电场线的记忆:“光芒四射”正电荷,“万箭穿心”负电荷,等量同号“蝶双飞”,等量异号“灯光耀眼”
3. 静电平衡特点:
(1)导体内部场强处处为零。
(2)电荷只分布在导体的外表面上。
(3)导体表面任一点的场强方向与该处的表面垂直。
注意:在解答在静电平衡内容问题时,注意区分感应电荷产生的附加场强、外场强、合场强的区别与联系。
同步练习:
(答题时间:40分钟)
1. 把质量为m的正点电荷q在电场中从静止释放,在它运动过程中如果不计重力,下述说法中正确的是( )
A. 点电荷的运动轨迹必与电场线重合
B. 点电荷的速度方向必定和所在点的电场线的切线方向一致
C. 点电荷的加速度方向必定与所在点的电场线的切线方向一致
D. 点电荷的受力方向必与所在点的电场线的切线方向一致
2. 如图所示,两个带等量正电荷的小球A、B(可视为点电荷),被固定在光滑的绝缘水平面上。P、N是小球连线的中垂线上的两点,且PO=ON。现将一个电荷量很小的带负电的小球C(可视为质点),由P点静止释放,在小球C向N点运动的过程中,图中关于小球C的速度、加速度的图象,可能正确的是( )
3. 如图所示,A、B两点固定两个带相等电荷量的正点电荷,在A、B连线的中点C处放一点电荷(不计重力)。若给该点电荷一个初速度v0,v0方向与A、B连线垂直,则该点电荷的运动情况是( )
A. 如果C处的电荷为正电荷,则它可能做往复直线运动
B. 如果C处的电荷为负电荷,则它可能做往复直线运动
C. 如果C处的电荷为正电荷,则它做加速度先增大后减小、速度不断增大的直线运动
D. 如果C处的电荷为负电荷,则它做加速度先增大后减小、速度不断增大的直线运动
4. 将悬挂在细线上的带正电的小球A放在不带电的金属空心球C内(不与球接触),另有一个悬挂在细线上的带负电的小于B向C靠近,如图所示,于是有( )
A. A向左偏离竖直方向,B向右偏离竖直方向
B. A的位置不变,B向右偏离竖直方向
C. A向左偏离竖直方向,B的位置不变
D. A和B的位置都不变
5. 如图所示是某静电场的一部分电场线分布情况,下列说法中正确的是( )
A. 这个电场可能是负点电荷的电场
B. 点电荷q在A点处受到的静电力比在B点处受到的静电力大
C. 点电荷q在A点处的瞬时加速度比在B点处的瞬时加速度小(不计重力)
D. 负电荷在B点处受到的静电力的方向沿B点切线方向
6. 有一接地的导体球壳,如图所示,球心处放一点电荷q,达到静电平衡时,则( )
A. q的电量变化时,球壳外电场随之改变
B. q在球壳外产生的电场强度为零
C. 球壳内、外表面的电荷在壳外的合场强为零
D. q与球壳内表面的电荷在壳外的合场强为零
*7. y轴上放置一块不带电的无限大接地金属板,现在x轴上的(L,0)点放一电荷量为q的正点电荷,它们之间的电场线分布如图甲所示。两个相距为2L的电荷量均为q的等量异种点电荷之间的电场线分布如图乙所示。某同学经过探究之后发现图甲所示的电场线分布与图乙中虚线(两点电荷连线的中垂线)右侧的电场线分布相同,求P(2L,0)点的电场强度的大小。
*8. 如图所示,在一足够大的空间内存在着水平向右的匀强电场,电场强度大小E=3.0×104 N/C。有一个质量m=4. 0×10-3 kg的带电小球,用绝缘轻细线悬挂起来,静止时细线偏离竖直方向的夹角θ=37°. 取g=10 m/s2,sin 37°=0. 60,cos 37°=0. 80,不计空气阻力的作用。
(1)求小球所带的电荷量及电性;
(2)如果将细线轻轻剪断,求细线剪断后,小球运动的加速度大小;
(3)从剪断细线开始经过时间t=0. 20 s,求这一段时间内小球电场力做的功。
答案:
1. 【答案】CD
【解析】正点电荷q由静止释放,如果电场线为直线,电荷将沿电场线运动,但电场线如果是曲线,电荷一定不沿电场线运动(因为如果沿电场线运动,其速度方向与受力方向重合,不符合曲线运动的条件),故A选项不正确;由于点电荷做曲线运动时,其速度方向与静电力方向不再一致(初始时刻除外),故B选项不正确;而点电荷的加速度方向,也即电荷所受静电力方向必与该点电场强度方向一致,即与所在点的电场线的切线方向一致,故C、D选项正确。
2. 【答案】BC
【解析】小球C向N点运动过程中,受到的静电力是变力,在中点O时受力为零,所以速度—时间图象不是直线,A错误,B可能;由牛顿第二定律结合库仑定律可知C可能,D错误。
3. 【答案】BC
【解析】带相等电荷量的两个正电荷中垂线上的场强变化情况是,C点合场强为零,从C向外电强度先变大后变小,电场强度方向向外。因此如果C处放点电荷为正电荷,则释放后点电荷先做加速度逐渐增大的加速运动,然后再做加速度逐渐减小的加速运动,故C正确;如果C处所放点电荷为负电荷,则点电荷先做加速度增大的减速运动,再做加速度减小的减速运动,当速度减为零时再向下加速,到C点后再向下减速,速度减为零后,再向上加速,做往复直线运动,故B正确。
4. 【答案】B
【解析】考虑B对A的作用时,A处在球壳C内,球壳C会对其内的A有屏蔽作用,使A不受B的作用。A通过静电感应使C的内、外壳分别带负电荷和正电荷,从而知道B受C外壳正电荷吸引,所以B往右偏离竖直方向,故B正确。
5. 【答案】B
【解析】电场线的疏密反映了电场强度的大小,而加速度的大小关键是看静电力的大小。判断A、B两处电场线的疏密是解答本题的关键。负点电荷的电场线是从四周无限远处不同方向指向负点电荷的直线,故A错;电场线越密的地方电场强度越大,由图知FA>FB,故B正确;由a=false知,a∝F,而F∝E,EA>EB,所以aA>aB,故C错;负电荷在B点受到的静电力的方向与B点电场强度的方向相反,故D错误。故选B。
6. 【答案】D
【解析】当导体球壳接地时,壳内电荷在壳外表面所产生的感应电荷流入大地,这时壳内电荷与壳内表面的感应电荷在壳内壁以外(包含导体壳层)任一点的合场强为零。故选项D正确。
7. 【答案】false
【解析】图甲所示的电场线分布与图乙中虚线(两点电荷连线的中垂线)右侧的电场线分布相同,因此P(2L,0)点的电场强度与乙图中正、负电荷连线上正电荷右侧L处电场强度相同,此处有两个电场,正电荷电场E1=false,方向向右,负电荷的电场E2=false,方向向左,两个电场的合电场强度就是P点电场强度E=E1-E2=false。
8. 【答案】(1)1. 0×10-6 C 正电荷 (2)12. 5 m/s2 (3)4. 5×10-3 J
【解析】(1)小球受到重力mg、电场力F和细线的拉力T的作用,
如图所示,由共点力平衡条件有:
F=qE=mgtan θ
解得:q=false =1. 0×10-6 C
电场力的方向与电场强度的方向相同,故小球所带电荷为正电荷。
(2)剪断细线后,小球做匀加速直线运动,设其加速度为a,由牛顿第二定律有:false=ma
解得:a=false=12. 5 m/s2.
(3)在t=0. 20 s的时间内,小球的位移为:
l=falseat2=0. 25 m
小球运动过程中,电场力做的功为:
W=qElsin θ=mglsin θtan θ=4. 5×10-3 J
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
