平行四边形的性质1

(共10张PPT)
1.3平行四边形的性质1
教学目标
1.会证明平行四边形的性质,会利用性质解决有关的数学问题;
2.通过用全等来证明平行四边形的性质,感受数学中转化思想的应用;
动动脑,回忆一下
平行四边形的定义是什么
两组对边分别_____四边形叫做平行四边形;
根据平行四边形的定义可知,平行四边形的两组对边_______;
平行四边形 矩形 菱形 正方形
对边平行
对边相等
四边相等
对角相等
4个角是直角
对角线互相平分
对角线相等
对角线互相垂直
两条对角线平分两组对角
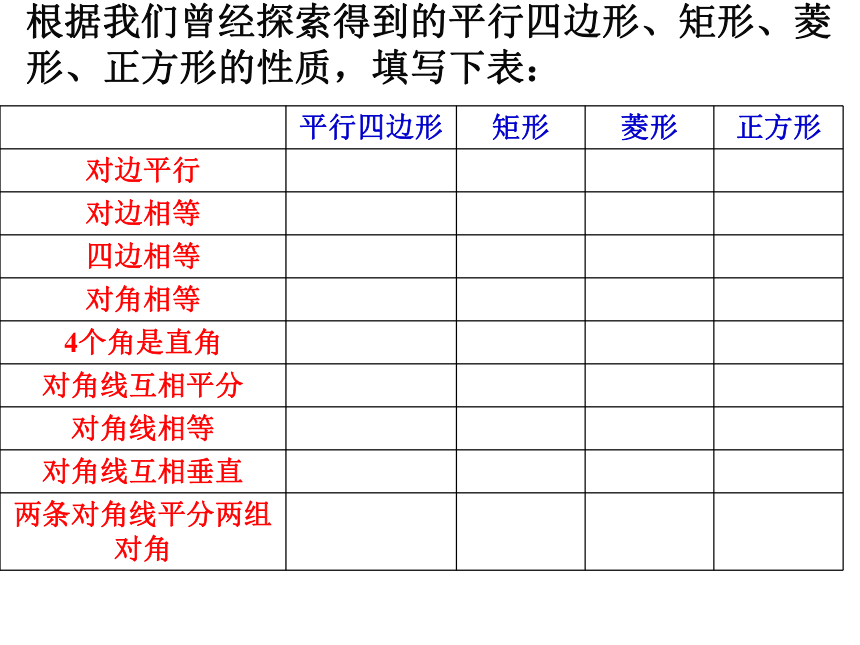
根据我们曾经探索得到的平行四边形、矩形、菱形、正方形的性质，填写下表：
再努力一下
除了由定义得到的性质(两组对边分别平行),平行四边形还有哪些性质
平行四边形的两组对边________;
平行四边形的两组对角________;
平行四边形的对角线__________;
思考与表达
怎样想 怎样写
要证AO=CO，BO=DO
只需证△AOB≌△COD
只需证AB=CD
只需证△ABC≌△CDA
已知，如图，在平行四边形ABCD中，对角线AC、BD相交于点O，
求证：AO=CO，BO=DO
例1 ：已知：如图，□ ABCD中，E、F分别是DC、AB的中点。求证：AE=CF
若将例1中的“E、F分别是DC、AB的中点”改为“DE=1/3DC，BF=1/3AB
是否还能得到同样的结论？
例2、 证明“夹在两条平行线之间的平行线段相等”
分析：根据命题先画出相应图形，再由命题与所画图形写出已知、求证，最后根据已知条件写出证明过程。
例3如图，四边形ABCD是平行四边形，点F在BA的延长线上，连结CF交于AD点E．
求证：(1)△CDE∽△FAE
(2)当E是AD的中点，且BC=2CD时，求证：∠F=∠BCF
四、小结：
1、平行四边形对边相等，对角相等，邻角互补，对角线互相平分。
2、是中心对称图形，两条对角线的交点是对称中心。
3、平行线之间的距离处处相等。