平行四边形性质训练

(共9张PPT)
平行四边形性质训练
选择题：
1. ABCD中,∠A比∠B大20°则∠C的度数为( )
A、60 ° B、80 °C、100°D、120°
2. ABCD的周长为40cm,⊿ABC的周长为25cm,则对角 线AC长为( )
A.5cm B.15cm C. 6cm D. 16cm
ABCD中,∠ A=43 ° ,过点A作BC和CD的垂线，那么这两条垂线的夹角度数为 ( )
A、113° B、115 ° C、137°D、90°
C
A
C
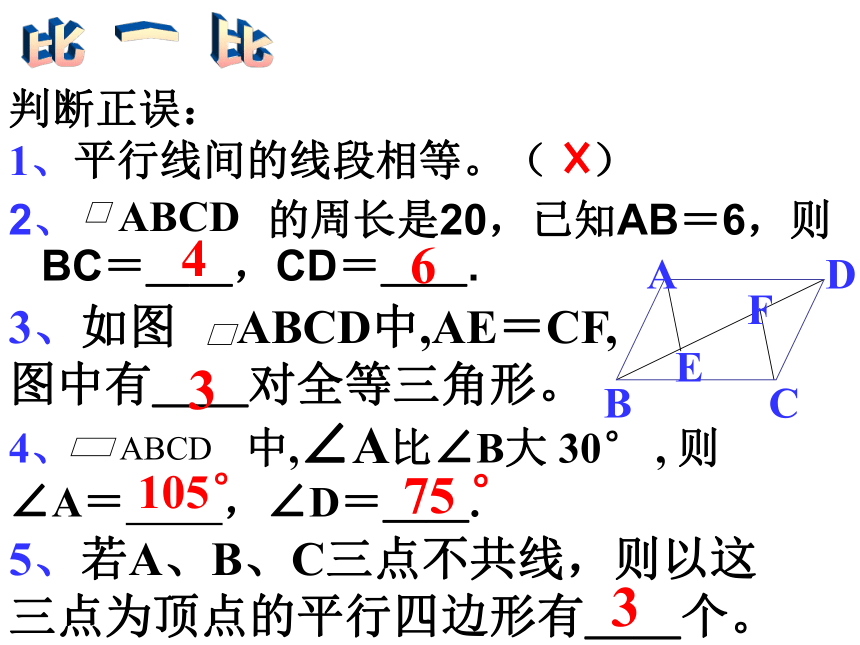
2、 的周长是20，已知AB＝6，则BC＝＿＿，CD＝＿＿.
判断正误：
1、平行线间的线段相等。（ ）
3、如图 ABCD中,AE＝CF,图中有＿＿对全等三角形。
4
ABCD
A
D
C
B
E
F
6
3
4、 中,∠A比∠B大 30° , 则∠A＝ ，∠D＝＿＿.
ABCD
5、若A、B、C三点不共线，则以这三点为顶点的平行四边形有＿＿个。
3
105°
75 °
M
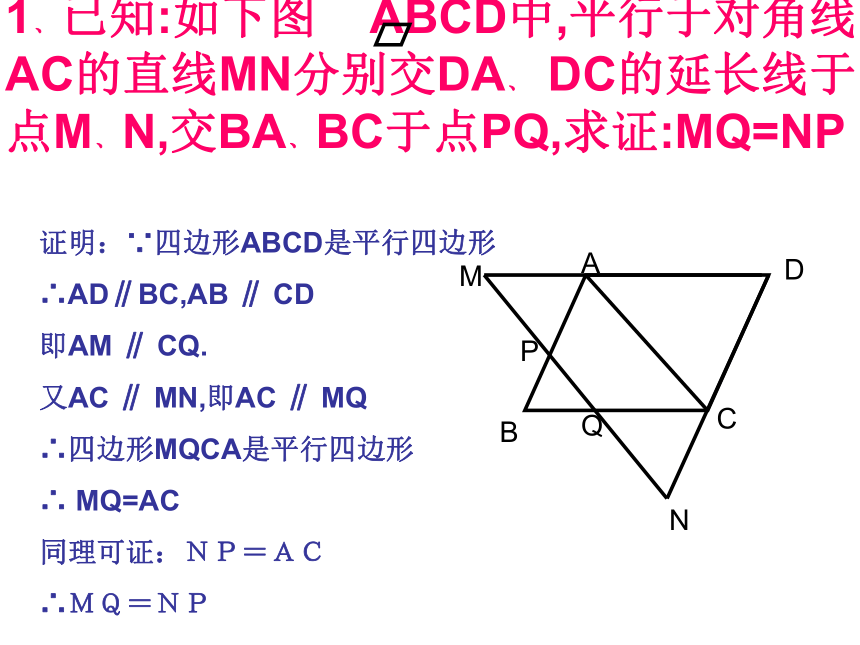
1﹑已知:如下图 ABCD中,平行于对角线AC的直线MN分别交DA﹑ DC的延长线于点M﹑N,交BA﹑BC于点PQ,求证:MQ=NP
A
D
B
N
Q
C
P
证明：∵四边形ABCD是平行四边形
∴AD∥BC,AB ∥ CD
即AM ∥ CQ.
又AC ∥ MN,即AC ∥ MQ
∴四边形MQCA是平行四边形
∴ MQ=AC
同理可证：ＮＰ＝ＡＣ
∴ＭＱ＝ＮＰ
2.已知 ABCD中,AE⊥BD,AF⊥BD,垂足为E、F,
求证：EB=DF
A
B
C
D
E
F
证明：∵AE⊥BD，CF ⊥ BD
∴∠AEB=90°，∠CFD=90°
∴∠ AEB=∠CFD
又四边形ABCD是平行四边形
∴ AB=CD，∠ABE=∠CDF
∴ ⊿ABE≌⊿CDF
∴ BE=DF
ABCD中,∠A=150°,AB=8cm,
BC=10cm,
求：四边形ABCD的面积
A
B
C
D
E
解：过点A作AE ⊥ BC交BC于E。
∵四边形ABCD是平行四边形，
∴AD∥BC
∴∠BAD+∠B=180°
∵ ∠BAD=150 °
∴∠B=30 °
在Rt⊿ABE中，∠B=30 °
∴AE= AB=4， ∴ S ABCD=4×10=40（cm)
已知如图,在 ABCD中,AC与BD相交于点O,点E、F在AC上,且BE∥DF。
求证：BE=DF
A
B
C
D
O
E
F
证明：∵BE∥DF
∴∠BEO=∠DFO（ ）
∵四边形ABCD是平行四边形
∴OB=OD （ ）
又∠BOE=∠DOF
∴⊿BOE≌⊿DOF （ ）
∴BE=DF （ ）
如图：在 ABCD中，O是对角线AC和BD的交点，OE⊥AD于E，OF⊥BC于F。
求证：OE=OF
A
B
C
D
E
F
O
证明： ∵ OE⊥AD， OF⊥BC，
∴∠AEO=∠CFO=90 °
∵ 四边形ABCD为平行四边形
∴OA=OC（ ）
AD ∥ BC
∴∠ DAC=∠ACB，
∴ ⊿ AEO ≌⊿ CFO（AAS）
∴ OE=OF
已知如图: ABCD中,E为CD的中
点,连结BE并延长交AD的延长线于
点F.
A
B
C
D
E
F
(1)求证:BE=EF
(2)当 ABCD的边
长满足什么条件时,
有∠F=∠ABC