人教版九年级上数学22.2二次函数与一元二次方程的关系课件(16张)
文档属性
| 名称 | 人教版九年级上数学22.2二次函数与一元二次方程的关系课件(16张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 00:00:00 | ||
图片预览




文档简介
白石中学 邱衍平
要点回顾
y=ax2+bx+c的图象和x轴交点
方程ax2+bx+c=0的根
b2-4ac
函数的图象
有两个交点
方程有两个不相等的实数根
b2-4ac > 0
只有一个交点
方程有两个相等的实数根
b2-4ac = 0
没有交点
方程没有实数根
b2-4ac < 0
x
y
o
.
.
x
y
o
x
y
o
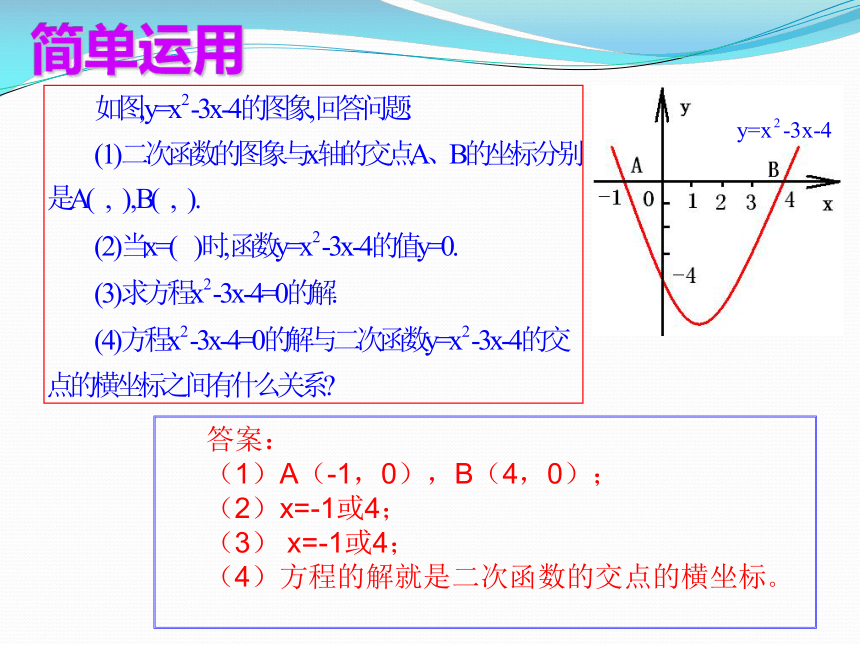
简单运用
答案:
(1)A(-1,0),B(4,0);
(2)x=-1或4;
(3) x=-1或4;
(4)方程的解就是二次函数的交点的横坐标。
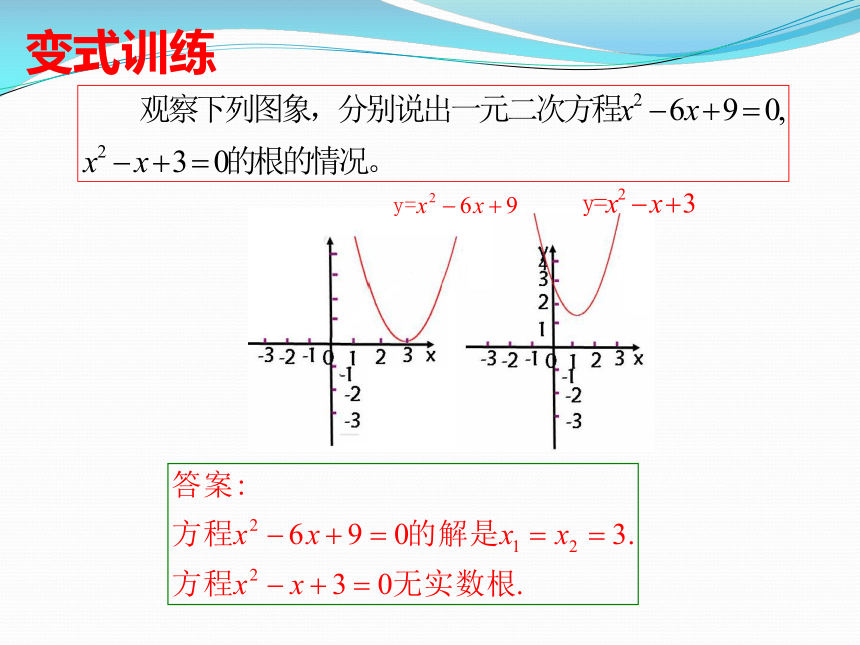
变式训练
例题精析
小试牛刀
答案:
(1)△>0,函数的图象与x轴有两个交点;
(2)△=0,函数的图象与x轴有一个交点;
(3)△<0,函数的图象与x 轴没有交点。
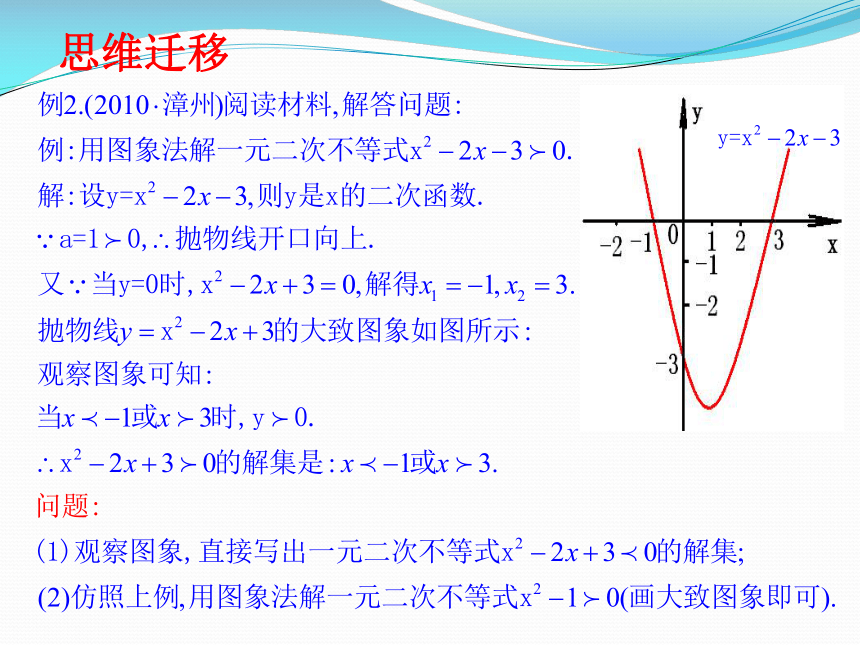
思维迁移
基础过关
B
D
能力提升
证明:∵△ =
=
=
又∵不论m为何值,
∴ >0
∴ △>0,
∴无论 m取何值,抛物线总与x轴有两个交点.
5.已知二次函数 的图像与X轴有两个不同的交点.
(1) 求k的取值范围
(2) 当k为何值时,这两个交点横坐标的平方和等于50.
能力提升
解:△=
∵ >0
∴k的取值为
解:
解之得:
k的取值为
∴k的值为±1.
要点小结
一般地,关于x的一元二次方程ax2+bx+c=0(a≠0)的根就是二次函数y=ax2+bx+c(a≠0)的值为0时自变量x的值,也就是函数y=ax2+bx+c的图象与x轴交点的横坐标。
可由一元二次方程的根的判别式来判定二次函数图象与x轴的交点的情况,由根与系数的关系来解决相关问题。
在函数问题中,往往需要解方程:反过来也可以利用函数图象解方程。
课后练习
祝同学们学心进步!
共同进步!
2019
ppt资料
*
欢迎批评指导!!
要点回顾
y=ax2+bx+c的图象和x轴交点
方程ax2+bx+c=0的根
b2-4ac
函数的图象
有两个交点
方程有两个不相等的实数根
b2-4ac > 0
只有一个交点
方程有两个相等的实数根
b2-4ac = 0
没有交点
方程没有实数根
b2-4ac < 0
x
y
o
.
.
x
y
o
x
y
o
简单运用
答案:
(1)A(-1,0),B(4,0);
(2)x=-1或4;
(3) x=-1或4;
(4)方程的解就是二次函数的交点的横坐标。
变式训练
例题精析
小试牛刀
答案:
(1)△>0,函数的图象与x轴有两个交点;
(2)△=0,函数的图象与x轴有一个交点;
(3)△<0,函数的图象与x 轴没有交点。
思维迁移
基础过关
B
D
能力提升
证明:∵△ =
=
=
又∵不论m为何值,
∴ >0
∴ △>0,
∴无论 m取何值,抛物线总与x轴有两个交点.
5.已知二次函数 的图像与X轴有两个不同的交点.
(1) 求k的取值范围
(2) 当k为何值时,这两个交点横坐标的平方和等于50.
能力提升
解:△=
∵ >0
∴k的取值为
解:
解之得:
k的取值为
∴k的值为±1.
要点小结
一般地,关于x的一元二次方程ax2+bx+c=0(a≠0)的根就是二次函数y=ax2+bx+c(a≠0)的值为0时自变量x的值,也就是函数y=ax2+bx+c的图象与x轴交点的横坐标。
可由一元二次方程的根的判别式来判定二次函数图象与x轴的交点的情况,由根与系数的关系来解决相关问题。
在函数问题中,往往需要解方程:反过来也可以利用函数图象解方程。
课后练习
祝同学们学心进步!
共同进步!
2019
ppt资料
*
欢迎批评指导!!
同课章节目录
