沪科版 2020年九年级上册22.2相似三角形的判定练习(Word版 含解析)
文档属性
| 名称 | 沪科版 2020年九年级上册22.2相似三角形的判定练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 386.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 06:29:58 | ||
图片预览



文档简介
22.2相似三角形的判定
1.如图20-K-3,F是?ABCD的对角线BD上的一点,BF∶FD=1∶3,则BE∶EC的值为( )
图20-K-3
A.
B.
C.
D.
2.2018·南充
如图20-K-6,在△ABC中,DE∥BC,BF平分∠ABC,交DE的延长线于点F.若AD=1,BD=2,BC=4,则EF=________.
图20-K-6
3.如图20-K-7,AC∥BD,AD,BC相交于点E,EF∥BD.求证:+=
图20-K-7
4.如图21-K-1,在△ABC中,∠AED=∠B,则下列等式成立的是( )
A.=
B.=
C.=
D.=
图21-K-1
5.如图21-K-2,在△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD∶DC=5∶3,则DE的长为( )
A.
B.
C.
D.
6.如图21-K-3,在矩形ABCD中,将△ABF沿着AF折叠,点B恰好落在DC边上的点E处,则一定有( )
A.△ADE∽△ECF
B.△ECF∽△AEF
C.△ADE∽△AEF
D.△AEF∽△AFB
图21-K-3
7.2018·包头改编如图21-K-6,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,求DF的长.
图21-K-6
8.2017·合肥54中一模如图22-K-3,△ACD和△ABC相似需具备的条件是( )
A.=
B.=
C.AC2=AD·AB
D.CD2=AD·BD
图22-K-3
9.如图22-K-5,在△ABC中,AB=6,AC=4,P是AC的中点,过点P的直线交AB于点Q.若以A,P,Q为顶点的三角形与△ABC相似,则AQ的长为( )
A.3
B.3或
C.3或
D.
图22-K-5
10.已知等腰三角形ABC的两边长分别是4和9,等腰三角形DEF的腰长为6,则当它的底边长为________时,等腰三角形ABC和等腰三角形DEF相似.
11.2018·肥东县月考
如图23-K-2,在矩形ABEF中,四边形ABCH、四边形CDGH和四边形DEFG都是正方形.
(1)求证:△ACD∽△ECA;
(2)求∠AED与∠ADC的度数和.
图23-K-2
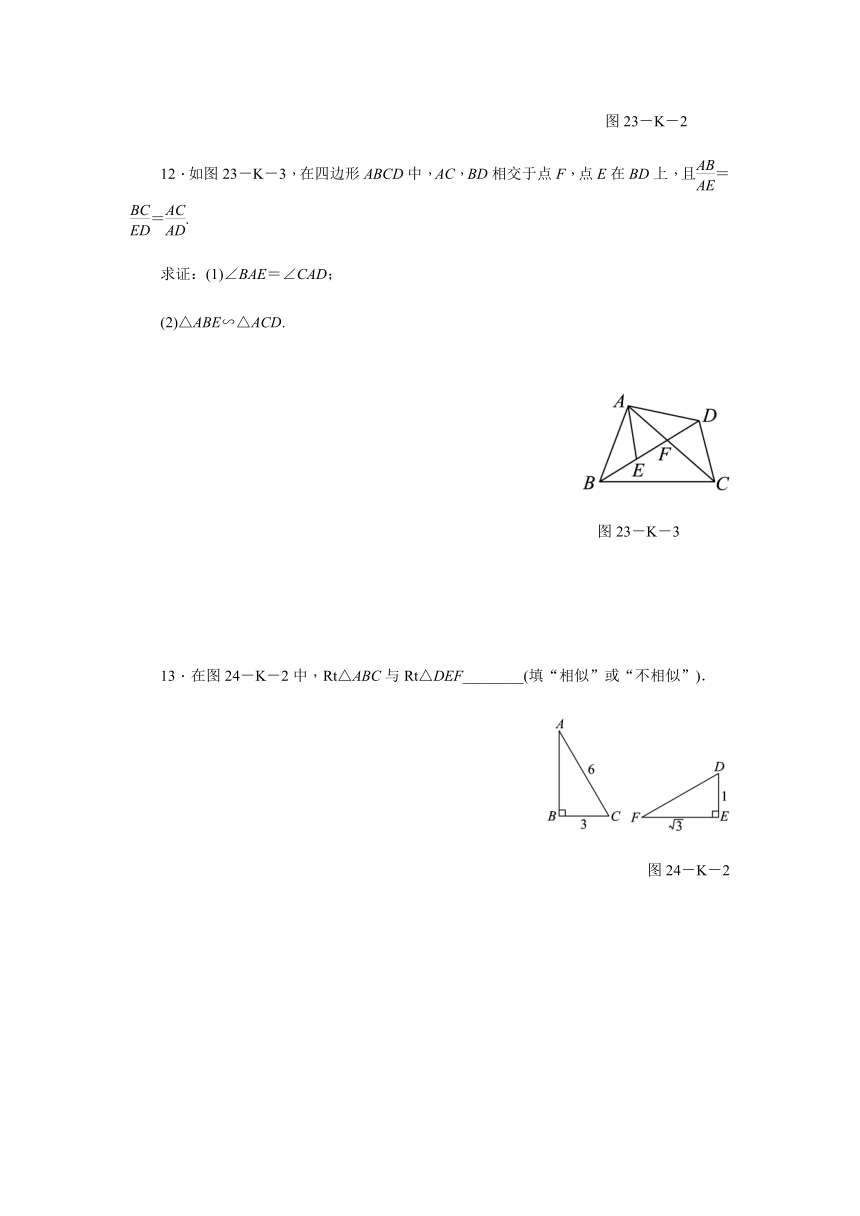
12.如图23-K-3,在四边形ABCD中,AC,BD相交于点F,点E在BD上,且==.
求证:(1)∠BAE=∠CAD;
(2)△ABE∽△ACD.
图23-K-3
13.在图24-K-2中,Rt△ABC与Rt△DEF________(填“相似”或“不相似”).
图24-K-2
1.[解析]
A ∵四边形ABCD是平行四边形,
∴AD=BC,BE∥AD,∴△BEF∽△DAF,
∴BE∶DA=BF∶DF=1∶3,∴BE∶BC=1∶3,∴BE∶EC=1∶2.
2.[答案]
[解析]
∵DE∥BC,∴∠F=∠FBC.
∵BF平分∠ABC,∴∠DBF=∠FBC,
∴∠F=∠DBF,∴DF=BD=2.
∵DE∥BC,∴△ADE∽△ABC,
∴=,即=,
解得DE=,
∴EF=DF-DE=2-=,
故答案为.
3.证明:∵AC∥BD∥EF,
∴△BEF∽△BCA,△AEF∽△ADB,
∴=,=,
∴+=+==1,
∴+=.
4.[解析]
C 根据“一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似”可以判定△ADE∽△ACB,再根据相似三角形的对应边成比例,可知等式=正确.
5.[解析]
D ∵BD∶DC=5∶3,BC=8,∴BD=5,DC=3.∵∠ADC=∠BDE,
∠C=∠E,
∴△ADC∽△BDE,∴=,即=,解得DE=.
6.[解析]
A 根据题意可知,∠DAE+∠AED=∠AED+∠CEF=90°,∴∠DAE=∠CEF.
又∵∠D=∠C=90°,∴△ADE∽△ECF.
7.解:如图,连接DE.
在Rt△BDC中,BC=4,∠DBC=30°,
∴DC=BC=2,由勾股定理得BD=2
.
∵∠BDC=90°,E是BC的中点,
∴DE=BE=CE=BC=2.
∵∠DBC=30°,∴∠BDE=∠DBC=30°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠ABD=∠BDE,∴DE∥AB,
∴△DEF∽△BAF,∴=.
在Rt△ABD中,∠ABD=30°,BD=2
,
∴AD=,由勾股定理得AB=3,
∴==,∴=,
∴DF=BD=×2
=.
8.[解析]
C 在△ACD和△ABC中,∠A=∠A,根据两边成比例,且夹角相等的两个三角形相似,得添加的条件是=,
∴AC2=AD·AB.
9.[解析]
B 已知∠A是公共角,则当=或=时,可满足题目要求,解得AQ=3或AQ=.
10.[答案]
[解析]
∵等腰三角形ABC的两边长分别是4和9,4+4<9,
∴等腰三角形ABC的腰长是9,底边长为4.
∵等腰三角形DEF的腰长为6.
设等腰△DEF的底边长为x,则有=,
∴x=.
11.解:(1)证明:设AB=1,则三个正方形的边长均为1.由图及勾股定理,得AC=,CD=1,AD=,EC=2,EA=.
∵===,
∴△ACD∽△ECA.
(2)由(1)可知∠AED=∠CAD,
∴∠AED+∠ADC=∠CAD+∠ADC=∠ACB=45°.
12.证明:(1)在△ABC与△AED中,
∵==,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAC-∠EAF=∠EAD-∠EAF,
即∠BAE=∠CAD.
(2)∵=,
∴=.
在△ABE与△ACD中,
∵∠BAE=∠CAD,=,
∴△ABE∽△ACD.
13.相似
1.如图20-K-3,F是?ABCD的对角线BD上的一点,BF∶FD=1∶3,则BE∶EC的值为( )
图20-K-3
A.
B.
C.
D.
2.2018·南充
如图20-K-6,在△ABC中,DE∥BC,BF平分∠ABC,交DE的延长线于点F.若AD=1,BD=2,BC=4,则EF=________.
图20-K-6
3.如图20-K-7,AC∥BD,AD,BC相交于点E,EF∥BD.求证:+=
图20-K-7
4.如图21-K-1,在△ABC中,∠AED=∠B,则下列等式成立的是( )
A.=
B.=
C.=
D.=
图21-K-1
5.如图21-K-2,在△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD∶DC=5∶3,则DE的长为( )
A.
B.
C.
D.
6.如图21-K-3,在矩形ABCD中,将△ABF沿着AF折叠,点B恰好落在DC边上的点E处,则一定有( )
A.△ADE∽△ECF
B.△ECF∽△AEF
C.△ADE∽△AEF
D.△AEF∽△AFB
图21-K-3
7.2018·包头改编如图21-K-6,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,求DF的长.
图21-K-6
8.2017·合肥54中一模如图22-K-3,△ACD和△ABC相似需具备的条件是( )
A.=
B.=
C.AC2=AD·AB
D.CD2=AD·BD
图22-K-3
9.如图22-K-5,在△ABC中,AB=6,AC=4,P是AC的中点,过点P的直线交AB于点Q.若以A,P,Q为顶点的三角形与△ABC相似,则AQ的长为( )
A.3
B.3或
C.3或
D.
图22-K-5
10.已知等腰三角形ABC的两边长分别是4和9,等腰三角形DEF的腰长为6,则当它的底边长为________时,等腰三角形ABC和等腰三角形DEF相似.
11.2018·肥东县月考
如图23-K-2,在矩形ABEF中,四边形ABCH、四边形CDGH和四边形DEFG都是正方形.
(1)求证:△ACD∽△ECA;
(2)求∠AED与∠ADC的度数和.
图23-K-2
12.如图23-K-3,在四边形ABCD中,AC,BD相交于点F,点E在BD上,且==.
求证:(1)∠BAE=∠CAD;
(2)△ABE∽△ACD.
图23-K-3
13.在图24-K-2中,Rt△ABC与Rt△DEF________(填“相似”或“不相似”).
图24-K-2
1.[解析]
A ∵四边形ABCD是平行四边形,
∴AD=BC,BE∥AD,∴△BEF∽△DAF,
∴BE∶DA=BF∶DF=1∶3,∴BE∶BC=1∶3,∴BE∶EC=1∶2.
2.[答案]
[解析]
∵DE∥BC,∴∠F=∠FBC.
∵BF平分∠ABC,∴∠DBF=∠FBC,
∴∠F=∠DBF,∴DF=BD=2.
∵DE∥BC,∴△ADE∽△ABC,
∴=,即=,
解得DE=,
∴EF=DF-DE=2-=,
故答案为.
3.证明:∵AC∥BD∥EF,
∴△BEF∽△BCA,△AEF∽△ADB,
∴=,=,
∴+=+==1,
∴+=.
4.[解析]
C 根据“一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似”可以判定△ADE∽△ACB,再根据相似三角形的对应边成比例,可知等式=正确.
5.[解析]
D ∵BD∶DC=5∶3,BC=8,∴BD=5,DC=3.∵∠ADC=∠BDE,
∠C=∠E,
∴△ADC∽△BDE,∴=,即=,解得DE=.
6.[解析]
A 根据题意可知,∠DAE+∠AED=∠AED+∠CEF=90°,∴∠DAE=∠CEF.
又∵∠D=∠C=90°,∴△ADE∽△ECF.
7.解:如图,连接DE.
在Rt△BDC中,BC=4,∠DBC=30°,
∴DC=BC=2,由勾股定理得BD=2
.
∵∠BDC=90°,E是BC的中点,
∴DE=BE=CE=BC=2.
∵∠DBC=30°,∴∠BDE=∠DBC=30°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠ABD=∠BDE,∴DE∥AB,
∴△DEF∽△BAF,∴=.
在Rt△ABD中,∠ABD=30°,BD=2
,
∴AD=,由勾股定理得AB=3,
∴==,∴=,
∴DF=BD=×2
=.
8.[解析]
C 在△ACD和△ABC中,∠A=∠A,根据两边成比例,且夹角相等的两个三角形相似,得添加的条件是=,
∴AC2=AD·AB.
9.[解析]
B 已知∠A是公共角,则当=或=时,可满足题目要求,解得AQ=3或AQ=.
10.[答案]
[解析]
∵等腰三角形ABC的两边长分别是4和9,4+4<9,
∴等腰三角形ABC的腰长是9,底边长为4.
∵等腰三角形DEF的腰长为6.
设等腰△DEF的底边长为x,则有=,
∴x=.
11.解:(1)证明:设AB=1,则三个正方形的边长均为1.由图及勾股定理,得AC=,CD=1,AD=,EC=2,EA=.
∵===,
∴△ACD∽△ECA.
(2)由(1)可知∠AED=∠CAD,
∴∠AED+∠ADC=∠CAD+∠ADC=∠ACB=45°.
12.证明:(1)在△ABC与△AED中,
∵==,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAC-∠EAF=∠EAD-∠EAF,
即∠BAE=∠CAD.
(2)∵=,
∴=.
在△ABE与△ACD中,
∵∠BAE=∠CAD,=,
∴△ABE∽△ACD.
13.相似
