1.4.1 有理数的乘法 第1课时 课件(共23张PPT)
文档属性
| 名称 | 1.4.1 有理数的乘法 第1课时 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 21:28:27 | ||
图片预览






文档简介
人教版 七上
1.4.1有理数的乘法
第1课时
教学重点:
有理数乘法则的推导.
教学难点:
能运用法则进行有理数的乘法运算及实际应用.
复习回顾
在小学,我们已经学习正数及零的乘法运算.
(1).3╳5
(4).3╳0
计算:
引入负数后,怎样进行有理数的乘法运算呢?
如:(1).3╳(-5)=? (2).(-3)╳(-5)=?
=15
=0
探究新知
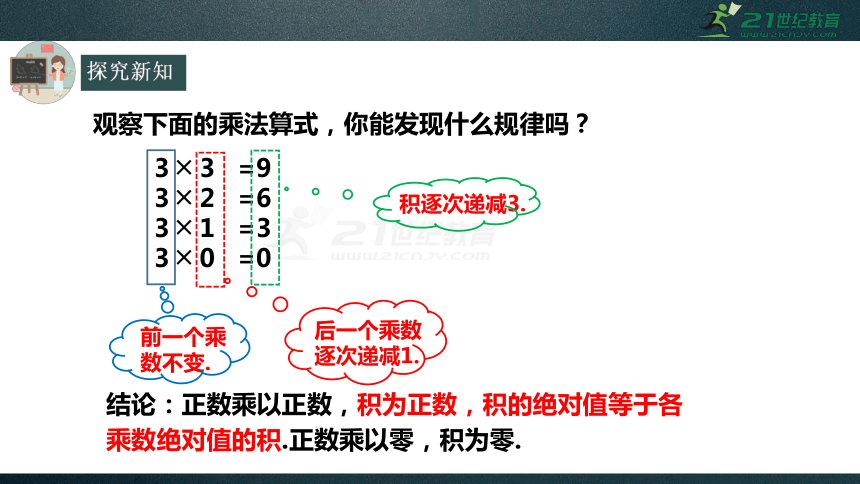
观察下面的乘法算式,你能发现什么规律吗?
3 ╳ 3 =9
3 ╳ 2 =6
3 ╳ 1 =3
3 ╳ 0 =0
后一个乘数逐次递减1.
前一个乘数不变.
积逐次递减3.
结论:正数乘以正数,积为正数,积的绝对值等于各乘数绝对值的积.正数乘以零,积为零.
探究新知
3 ╳ 3 = 9
3 ╳ 2 = 6
3 ╳ 1 = 3
3 ╳ 0 = 0
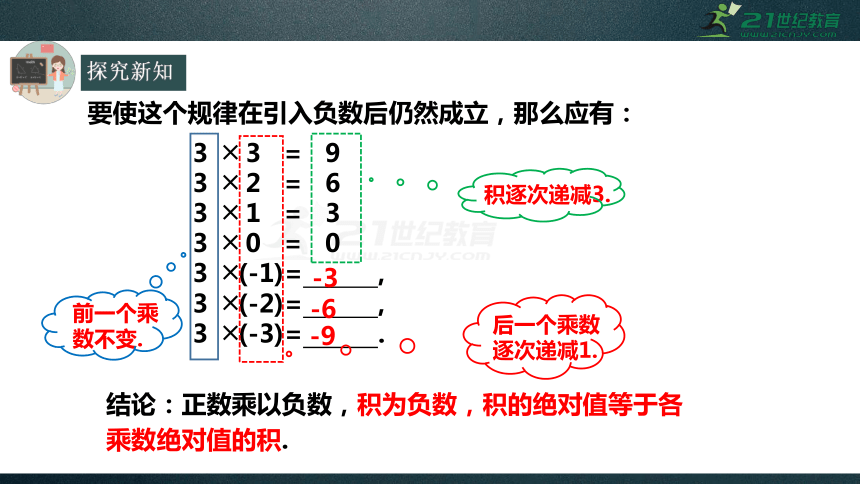
3 ╳(-1)= ,
3 ╳(-2)= ,
3 ╳(-3)= .
要使这个规律在引入负数后仍然成立,那么应有:
后一个乘数逐次递减1.
前一个乘数不变.
积逐次递减3.
-3
-6
-9
结论:正数乘以负数,积为负数,积的绝对值等于各乘数绝对值的积.
探究新知
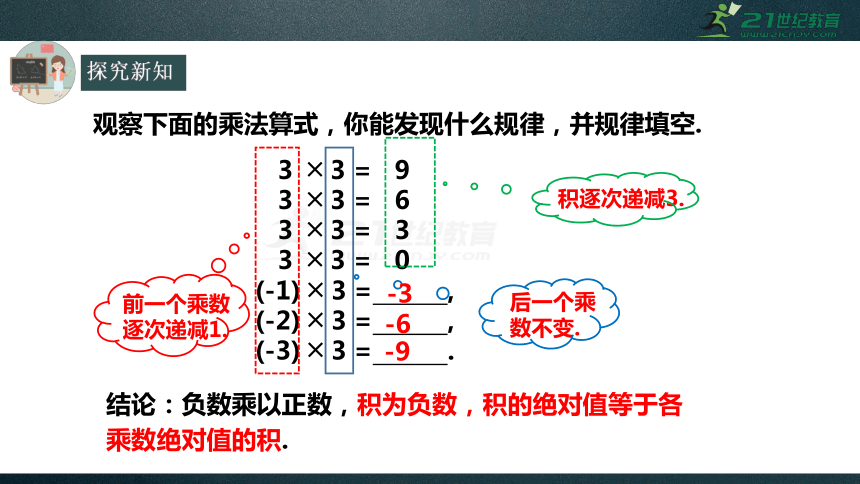
观察下面的乘法算式,你能发现什么规律,并规律填空.
3 ╳ 3 = 9
3 ╳ 3 = 6
3 ╳ 3 = 3
3 ╳ 3 = 0
(-1) ╳ 3 = ,
(-2) ╳ 3 = ,
(-3) ╳ 3 = .
前一个乘数逐次递减1.
后一个乘数不变.
积逐次递减3.
结论:负数乘以正数,积为负数,积的绝对值等于各乘数绝对值的积.
-3
-6
-9
归纳
从符号和绝对值两个角度观察上述算式,可以归纳如下:
①正数乘以正数,积为 ,积的绝对值等于各乘数绝对值的积.
②正数乘以负数,积为 ,积的绝对值等于各乘数绝对值的积.
③负数乘以正数,积为 ,积的绝对值等于各乘数绝对值的积.
正数
负数
负数
探究新知
利用上面归纳的结论计算下面的算式,你能发现什么规律.
(-3) ╳ 3 = ,
(-3) ╳ 2 = ,
(-3) ╳ 1 = ,
(-3) ╳ 0 = ,
(-3) ╳(-1) = ,
(-3) ╳(-2) = ,
(-3) ╳(-3) = .
按照上述规律,下面的空格可以各填什么数?从中可以归纳出什么结论?
规律:前一个乘数不变,后一个乘数逐次递减1,积逐次递增3.
-3
-6
-9
0
3
6
9
结论:负数乘以负数,积为正数,积的绝对值等于各乘数绝对值的积.
归纳总结
1.两数相乘,同号得正,异号得负并把绝对值相乘.
有理数的乘法法则:
2.任何数同0相乘,都得0.
如:(-3) ╳(-5)
(判断两数符号:同号是正数╳正数或负数╳负数)
=+( )
(确定积的符号:得正)
|-3|╳|-5|
(积的绝对值:两数绝对值的积)
=15
(-2) ╳6
(判断两数符号:异号是正数╳负数或负数╳正数)
(确定积的符号:得负)
(积的绝对值:两数绝对值的积)
=-( )
|-2|╳|6|
=-12
探究新知
(1).(-3) ×9 (2).8 ×(-1)
解:(1).(-3) ×9
(异号两数相乘)
(得负)
=-( )
3 ×9
(把绝对值相乘)
=-27
(2).8 ×(-1)
(异号两数相乘)
(得负)
=-( )
8 ×1
(把绝对值相乘)
=-8
1乘以一个数仍得这个数,-1乘以一个数得这个数的相反数.
探究新知
(同号两数相乘)
(得正)
=+( )
(把绝对值相乘)
=1
有理数的乘法运算一般步骤:
①判断两数的符号.
②确定积的符号.
③把绝对值相乘.
练一练
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}被乘数
乘数
积的符号
积的绝对值
结果
-5
-7
-3
4
8
-2
0.5
6
1.填写下表:
(1).(-12)×9 (2).(-5) ×(-6)
2.计算:
35
+35
+
12
-12
-
16
-16
-
3
+3
+
探究新知
解:(1).(-12)×9
(2).(-5) ×(-6)
=-(12×9)
=-108
=+(5×6)
=30
-5的倒数是 , 的倒数是 .
探究新知
观察上面两题有何特点?
两数相乘,它们的结果都是1.
有理数中仍然有:乘积是1的两个数互为倒数.
的倒数是 ,-2的倒数是 .
-2
-5
练一练
写出下面各数的倒数.
1的倒数是 -1 ,
-1的倒数是 1 ,
的倒数是 ,
的倒数是 ,
5的倒数是 ,
-5的倒数是 ,
的倒数是 ,
的倒数是 ,
0没有的倒数.
想一想,0有没有倒数?
练习小结
1.一个数和它的倒数符号相同,即正数的倒数是正数,负数
的倒数是负数.
2.倒数等于它本身的数有1或-1;
3.当ab=1, a叫做b的倒数,b叫做 a的倒数,倒数是相互的;
4.注意0没有倒数
5.求分数的倒数,只要把这个分数的分子,分母颠倒位置即可.
练习小结:
探究新知
例2 用正负数表示气温的变化量,上升为正,下降为负. 登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃.
课堂练习
(1).若a小于0,b大于0,则ab____0.
(2).若a小于0,b小于0,则ab_____0.
(3).若ab大于0,则a、b应满足 .
(4).若ab小于0,则a、b应满足 .
(5).倒数等于它本身的数是 ;
(6). a和b互为相反数,c和d互为倒数, 则a+b-3-cd= .
1.填空:
<
>
a、b是同号
a、b是异号
1和-1
-4
课堂练习
解:(1).(-8)×7
(2).(-3) ×(-7)
=-(8×7)
=-56
=+(3×7)
=21
(1).(-8)×7 (2).(-3) ×(-7)
2.计算:
课堂练习
3.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:规定:提价为正,降价为负.
(-5)×60=-300
答:销售额减少300元.
课堂小结
1.两数相乘,同号得正,异号得负并把绝对值相乘.
一.有理数的乘法法则:
2.任何数同0相乘,都得0.
二.1乘以一个数仍得这个数,-1乘以一个数得这个数的相反数.
三.乘积是1的两个数互为倒数.
注意事项:
1.法则只针对有两个因数相乘的情况.
2. 乘法运算的步骤是:观察两数的符号,然后确定积的符号,再确定积的绝对值.
课外作业
习题1.4
第37页第2题
第37页第3题
https://www.21cnjy.com/help/help_extract.php
1.4.1有理数的乘法
第1课时
教学重点:
有理数乘法则的推导.
教学难点:
能运用法则进行有理数的乘法运算及实际应用.
复习回顾
在小学,我们已经学习正数及零的乘法运算.
(1).3╳5
(4).3╳0
计算:
引入负数后,怎样进行有理数的乘法运算呢?
如:(1).3╳(-5)=? (2).(-3)╳(-5)=?
=15
=0
探究新知
观察下面的乘法算式,你能发现什么规律吗?
3 ╳ 3 =9
3 ╳ 2 =6
3 ╳ 1 =3
3 ╳ 0 =0
后一个乘数逐次递减1.
前一个乘数不变.
积逐次递减3.
结论:正数乘以正数,积为正数,积的绝对值等于各乘数绝对值的积.正数乘以零,积为零.
探究新知
3 ╳ 3 = 9
3 ╳ 2 = 6
3 ╳ 1 = 3
3 ╳ 0 = 0
3 ╳(-1)= ,
3 ╳(-2)= ,
3 ╳(-3)= .
要使这个规律在引入负数后仍然成立,那么应有:
后一个乘数逐次递减1.
前一个乘数不变.
积逐次递减3.
-3
-6
-9
结论:正数乘以负数,积为负数,积的绝对值等于各乘数绝对值的积.
探究新知
观察下面的乘法算式,你能发现什么规律,并规律填空.
3 ╳ 3 = 9
3 ╳ 3 = 6
3 ╳ 3 = 3
3 ╳ 3 = 0
(-1) ╳ 3 = ,
(-2) ╳ 3 = ,
(-3) ╳ 3 = .
前一个乘数逐次递减1.
后一个乘数不变.
积逐次递减3.
结论:负数乘以正数,积为负数,积的绝对值等于各乘数绝对值的积.
-3
-6
-9
归纳
从符号和绝对值两个角度观察上述算式,可以归纳如下:
①正数乘以正数,积为 ,积的绝对值等于各乘数绝对值的积.
②正数乘以负数,积为 ,积的绝对值等于各乘数绝对值的积.
③负数乘以正数,积为 ,积的绝对值等于各乘数绝对值的积.
正数
负数
负数
探究新知
利用上面归纳的结论计算下面的算式,你能发现什么规律.
(-3) ╳ 3 = ,
(-3) ╳ 2 = ,
(-3) ╳ 1 = ,
(-3) ╳ 0 = ,
(-3) ╳(-1) = ,
(-3) ╳(-2) = ,
(-3) ╳(-3) = .
按照上述规律,下面的空格可以各填什么数?从中可以归纳出什么结论?
规律:前一个乘数不变,后一个乘数逐次递减1,积逐次递增3.
-3
-6
-9
0
3
6
9
结论:负数乘以负数,积为正数,积的绝对值等于各乘数绝对值的积.
归纳总结
1.两数相乘,同号得正,异号得负并把绝对值相乘.
有理数的乘法法则:
2.任何数同0相乘,都得0.
如:(-3) ╳(-5)
(判断两数符号:同号是正数╳正数或负数╳负数)
=+( )
(确定积的符号:得正)
|-3|╳|-5|
(积的绝对值:两数绝对值的积)
=15
(-2) ╳6
(判断两数符号:异号是正数╳负数或负数╳正数)
(确定积的符号:得负)
(积的绝对值:两数绝对值的积)
=-( )
|-2|╳|6|
=-12
探究新知
(1).(-3) ×9 (2).8 ×(-1)
解:(1).(-3) ×9
(异号两数相乘)
(得负)
=-( )
3 ×9
(把绝对值相乘)
=-27
(2).8 ×(-1)
(异号两数相乘)
(得负)
=-( )
8 ×1
(把绝对值相乘)
=-8
1乘以一个数仍得这个数,-1乘以一个数得这个数的相反数.
探究新知
(同号两数相乘)
(得正)
=+( )
(把绝对值相乘)
=1
有理数的乘法运算一般步骤:
①判断两数的符号.
②确定积的符号.
③把绝对值相乘.
练一练
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}被乘数
乘数
积的符号
积的绝对值
结果
-5
-7
-3
4
8
-2
0.5
6
1.填写下表:
(1).(-12)×9 (2).(-5) ×(-6)
2.计算:
35
+35
+
12
-12
-
16
-16
-
3
+3
+
探究新知
解:(1).(-12)×9
(2).(-5) ×(-6)
=-(12×9)
=-108
=+(5×6)
=30
-5的倒数是 , 的倒数是 .
探究新知
观察上面两题有何特点?
两数相乘,它们的结果都是1.
有理数中仍然有:乘积是1的两个数互为倒数.
的倒数是 ,-2的倒数是 .
-2
-5
练一练
写出下面各数的倒数.
1的倒数是 -1 ,
-1的倒数是 1 ,
的倒数是 ,
的倒数是 ,
5的倒数是 ,
-5的倒数是 ,
的倒数是 ,
的倒数是 ,
0没有的倒数.
想一想,0有没有倒数?
练习小结
1.一个数和它的倒数符号相同,即正数的倒数是正数,负数
的倒数是负数.
2.倒数等于它本身的数有1或-1;
3.当ab=1, a叫做b的倒数,b叫做 a的倒数,倒数是相互的;
4.注意0没有倒数
5.求分数的倒数,只要把这个分数的分子,分母颠倒位置即可.
练习小结:
探究新知
例2 用正负数表示气温的变化量,上升为正,下降为负. 登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃.
课堂练习
(1).若a小于0,b大于0,则ab____0.
(2).若a小于0,b小于0,则ab_____0.
(3).若ab大于0,则a、b应满足 .
(4).若ab小于0,则a、b应满足 .
(5).倒数等于它本身的数是 ;
(6). a和b互为相反数,c和d互为倒数, 则a+b-3-cd= .
1.填空:
<
>
a、b是同号
a、b是异号
1和-1
-4
课堂练习
解:(1).(-8)×7
(2).(-3) ×(-7)
=-(8×7)
=-56
=+(3×7)
=21
(1).(-8)×7 (2).(-3) ×(-7)
2.计算:
课堂练习
3.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:规定:提价为正,降价为负.
(-5)×60=-300
答:销售额减少300元.
课堂小结
1.两数相乘,同号得正,异号得负并把绝对值相乘.
一.有理数的乘法法则:
2.任何数同0相乘,都得0.
二.1乘以一个数仍得这个数,-1乘以一个数得这个数的相反数.
三.乘积是1的两个数互为倒数.
注意事项:
1.法则只针对有两个因数相乘的情况.
2. 乘法运算的步骤是:观察两数的符号,然后确定积的符号,再确定积的绝对值.
课外作业
习题1.4
第37页第2题
第37页第3题
https://www.21cnjy.com/help/help_extract.php
